基于柔刚体模型的高速车轮振动辐射噪声研究

陈士杰,陆正刚

(1 同济大学 汽车学院,上海201804;2 同济大学 铁道与城市轨道交通研究院,上海201804)

随着轨道交通工具的迅速发展,轨道车辆运行噪声已成为城市噪声的主要来源之一。国内外的各种研究文献显示,当列车速度低于250 km/h时,铁路噪声以轮轨噪声为主。目前,随着轨道车辆速度的不断提升,我国铁路客车的运行速度在200 km/h左右,货车速度大约为120 km/h,城市轨道交通列车的最高运行速度一般为80km/h,因此,目前我国铁路及城市轨道交通的噪声主要以轮轨噪声为主。在轮轨系统中,车轮振动辐射噪声又是最主要的噪声源之一,本文在传统噪声预测模型的基础上,将柔性轮对模块引入动力学模型,并对车轮结构进行优化设计,从而降低车轮振动辐射噪声。

1 轮轨噪声产生机理

轮轨噪声是由于轨道结构钢轨表面的短波不平顺激发轮轨振动并通过空气传播而产生的。轮轨表面的不平顺波长为2～6 cm,不平顺幅值可达0.25 mm。列车在磨耗钢轨上运行时,会激发一种典型的颤噪声,其频率与速度有关,即为轮轨噪声。

轮轨噪声包括钢轨与车轮之间受迫振动而产生的滚动噪声,车轮经过钢轨接头处产生的撞击声以及车轮过弯道时挤压外轨而产生的摩擦噪声。轮轨噪声的能量主要集中在频率1 000～2 500 Hz范围内,由于其分布范围广,对环境影响大,故已成为我国高速铁路噪声的主要来源。

2 轮轨噪声预测模型

普遍认为轮轨噪声是由于轮轨接触表面的不平顺产生的。当轮对在轨道上滚动时,这种不平顺导致轮轨的相对运动以及轮轨本身的弹性振动,这种弹性振动向空气中辐射就变成了噪声。除了轮轨这两个噪声源以外,轨枕、车体和道砟也产生噪声,但后者一般处于次要地位。噪声预测模型以轮轨表面不平顺作为激扰源,采用“轮轨振动—轮轨声辐射—轮轨噪声”这一思路展开研究,其预测模型示意图如图1所示。轮轨在载荷作用下要发生弹性变形,因此轮轨之间形成了一个接触区,当轮轨表面粗糙度波长小于接触区尺寸时,轮轨接触后,轮轨表面粗糙度对轮轨的激励作用不受影响,从而形成接触滤波。

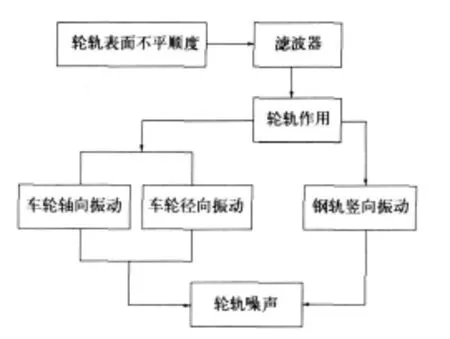
图1 轮轨噪声预测模型示意图

由图1可知,钢轨及车轮的辐射噪声共同构成轮轨噪声的振动源。在研究轮轨相互作用力时,假定轮轨接触力与相对接触位移遵循赫兹公式。由于钢轨与地基固结紧密,其横向振动很小,故只考虑其竖向振动效应;车轮振动包括轴向和径向两个方向,对噪声均有较大影响,因此需综合考虑。

由于对钢轨的振动辐射噪声国内外已有专家学者作了大量的研究,故此处主要对车轮振动辐射噪声进行分析。

设单个车轮通过钢轨引起的振动传播到离钢轨距离为d的一点的声压为p,其声压均方值为＜p2＞T,有

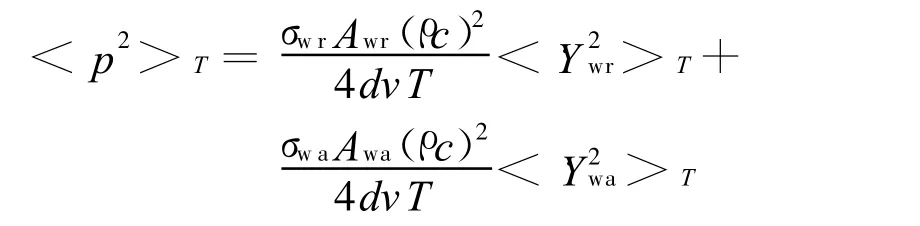
3 轮对作用力仿真

在传统的模拟仿真研究方法中,车轮振动辐射噪声的研究多基于使用刚性轮对模块建立的动力学模型,但刚性轮对在研究过程中有明显的缺陷,即其无法模拟轮对的柔性变形,故对轮轨的变形及由此产生的振动辐射噪声无法进行合理有效的分析。本文在传统方法的基础上,结合了柔性多体系统动力学来进行研究。柔性多体系统动力学是研究可变形物体和刚体组成的柔刚体系统的动力学,其特点在于这种弹性变形和刚体运动之间的相互作用及耦合效应。

根据拉格朗日方程可建立车辆柔性多体系统的动力学方程,对这种弱耦合、强非线性微分方程进行数值分析。以轮对为例,计算其研究频率范围内的各阶模态,可得到对应的各阶振型;将振型作为固有属性赋予轮对模型,从而形成柔性模块。在动力学软件中对轨道车辆进行动态仿真,此处以重车工况为例,采用某一型号的轮对,车辆沿直线行驶,速度为160 km/h。

在1 000～2 500 Hz范围内,共有 35阶模态,由于模态振型不同,对辐射噪声的效果也有很大差别,现以其中影响最大的9阶模态作为研究频率。其振型及对应频率如图2所示。

在此条件下,将柔性轮对模块导入动力学模型进行动态仿真。以前转向架中的前轮对为研究对象,对应的左、右轮垂向轮轨接触力分别如图3、图4所示。

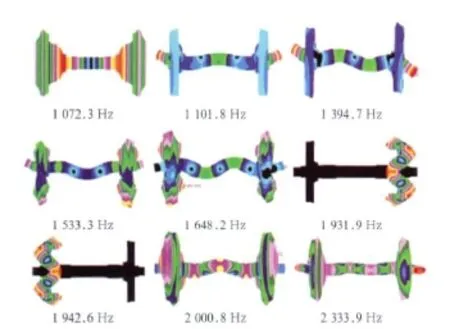
图2 轮对主要模态振型频率对应图

在此基础上,将仿真结果进行傅立叶变换,实现时频之间的转换,以便在频域内对噪声进行研究。傅立叶变换后结果如图5、图6所示,两图均采用双对数坐标系。

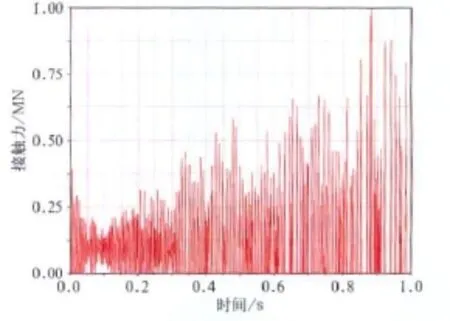
图3 左轮轮轨垂向接触力图

图4 右轮轮轨垂向接触力图

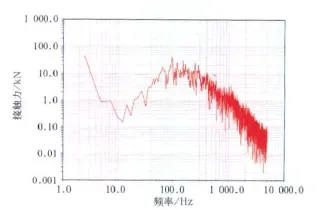
图5 左轮垂向接触力频域图

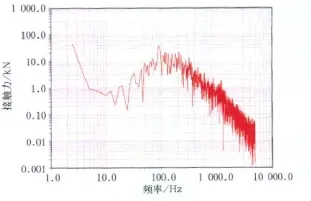
图6 右轮垂向接触力频域图

同理,通过动力学仿真可得到轮轨横向作用力、弹簧力及惯性力,将这些力分别作傅立叶变换,为保留其相位特性,傅立叶变换后结果用实部及虚部表示。

4 车轮辐射噪声及减噪措施分析

通过动力学仿真可获得轮轨作用力、惯性力等的变化曲线。将动力学模型计算结果作为激扰导入有限元软件进行计算,可得到一组频域内轮对结构振动响应速度值。

对于求解结构振动向周围空间的声辐射问题,本文主要采用的是直接边界元法。直接边界元法是结构表面的声压级和法向振动速度作为边界条件求解Helmholtz边界积分方程,其关键是求解下面的系统方程:

式中pj为流体模型表面上的节点压力;vn为流体模型表面法线方向上节点速度;A、B为影响矩阵。

流体模型表面上的声压、速度和声强等值在求解系统方程时,可以直接得到,要得到声场中任一点p处的声压,还需要计算下面的表达式:

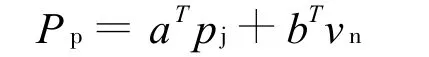
运用直接边界元法,将结构振动响应速度作为边界条件,并考虑空气介质对声辐射的影响,计算车轮辐射噪声的声压级。其中,测点距轮对几何中心8.5 m,距地面高度为1.35 m,计算频率为 1 000～4 000 Hz,计算结果如图7所示。

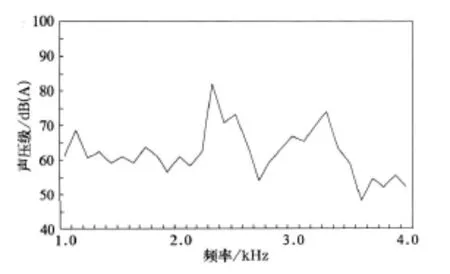
图7 车轮振动辐射噪声图

车轮辐射噪声的大小取决于车轮表面的结构振动响应,因此,车轮振动辐射噪声与车轮外形紧密相关。对车轮外形、结构进行优化,使之更为合理,不失为一种降噪的有效方法。

车轮主要由轮毂、辐板、轮辋3部分构成,为了研究车轮表面的振动响应,首先需要对3部分的结构进行研究。从理论上来说,车轮辐板处较为单薄,其横向振动对轴向噪声影响很大;而轮毂及轮辋对径向噪声起主要作用,但考虑到这两处承受的径向力较大,故不能轻易改变其结构。综上所述,为了达到降低车轮辐射噪声的最佳效果,首先选择对辐板进行优化改进。

由图 8可知,当辐板平均厚度由22 mm增加到26 mm时,车轮辐射噪声在2 000～4 000 Hz范围内有较为明显的降低,平均降噪幅度接近10 dB左右,当频率在2 000 Hz以下时,噪声降低的幅度较小;当辐板平均厚度继续增加到30 mm时,虽然在某些频率下噪声值继续降低,但声压级整体上与26 mm时相当。

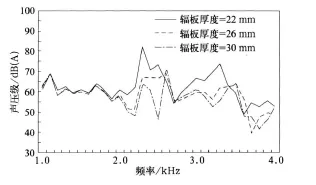
图8 改变辐板厚度时车轮振动辐射噪声比较图

由以上分析可知,增加辐板的厚度值虽然可以起到一定的降噪效果,但辐板厚度继续增大时,噪声并不会持续降低,且辐板变厚必然使轮对质量大幅增加,对列车的正常行驶产生较大影响,故考虑在不增加轮对质量的情况下,通过优化轮对外形而起到降噪的效果。

图9为原轮对与经过优化后的轮对截面比较图。对两种车轮辐射噪声计算结果如图10所示。由图10可知,通过轮对外形的优化,车轮辐射噪声有较为明显的降低,由于轮轨噪声的能量集中在1 000～2 500 Hz频率范围内,故在不增加轮对质量的前提下,通过优化轮对外形降低辐射噪声是一种可行的方法。此外,对比原轮对与优化后的轮对截面可知,原轮对接近于S型辐板轮,优化后的轮对采用直辐板形式,因此在轮对外形、质量基本相同的情况下,采用直辐板形式更有利于降低车轮辐射噪声。

随着轨道车辆减噪技术的迅速发展,在保留原轮对结构基本不变的基础上,通过增加阻尼装置来降低车轮辐射噪声已成为最新的研究方向。

图10 车轮形状优化前后辐射噪声比较图

图11为增加减噪块后的车轮结构图。增加的阻尼装置内包含橡胶层,可有效地吸收轮对的径向振动能量,从而降低车轮径向辐射噪声。

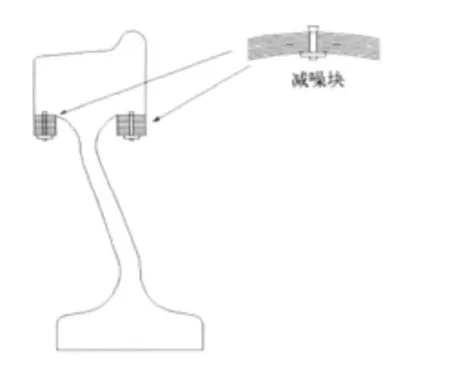
图11 带减噪块车轮结构图

通过噪声计算,可得到原轮对与带减噪块轮对辐射噪声的对比图,如图12所示。

由图12可知,减噪块对于降低车轮辐射噪声的效果较为明显,由于其基本保留原轮对的形状及结构不变,故可以在确保强度、刚度等基本性能不受影响的情况下起到降低车轮辐射噪声的效果,故已成为目前减噪的重要手段之一。

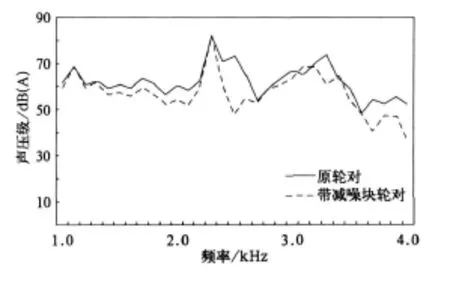
图12 车轮增加减噪块前后辐射噪声比较图

5 结束语

在车轮振动辐射噪声的计算过程中,轮对模型和激扰是关键。激扰的准确与否直接影响到噪声结果的精确度。通过使用柔性轮对模块建立动力学模型,可获得较为准确的激扰,并在此基础上,对车轮结构进行分析、优化,结果表明优化轮对结构对于降低车轮振动辐射噪声是一种较好的方法。此外,在车轮上附加减噪块对降低车轮径向辐射噪声亦是切实、可行的方法之一。

[1] 雷晓燕,圣小珍.铁路交通噪声与振动[M].北京:科学出版社,2004:166-210.

[2] 陆佑方.柔性多体系统动力学[M].北京:高等教育出版社,1996:181-230.

[3] 刘林芽,雷晓燕,练松良.轨道交通轮轨滚动噪声的预测[J],振动与冲击,2007,(12):146-150.

[4] 刘林芽,雷晓燕,练松良.车轮参数对轮轨噪声的影响[J],噪声与振动控制,2007,(5):74-77.

[5] 李增刚.SYSNOISE Rev5.6详解[M].北京:国防工业出版社,2005:9-11.