转向架横向稳定性的实时在线监测

刘 峰,延九磊,董孝卿,张瑞芳

(中国铁道科学研究院机车车辆研究所,北京100081)

从动力学角度看,高速列车之所以区别于普通列车的根本原因在于其所处的动态环境不同。随着列车速度的提高,其动态环境变化迅速,轮轨间动力作用加剧,这就要求车辆系统具有高的稳定性、良好的减振、隔振性能和运行安全性。

蛇行运动稳定性是车辆系统本身固有的属性,是决定客车能否高速运行的关键因素。可从阻尼的3种形态正、零、负的形式理解自激振动与系统固有参数的关系,即临界速度是车辆转向架的固有属性,当转向架设计完成后,其横向运动的临界速度是确定的,对于确定临界速度的高速列车其出厂时是完全满足构架横向稳定性要求的。这从各种验收试验及动力学计算等都可证明。随着转向架运行里程的不断增加,其横向稳定性约束条件会逐渐发生变化,如踏面磨耗的变化会影响踏面的等效锥度,节点的定位刚度也会随着运用发生变化,抗蛇行减振器等的参数也会发生相应的改变。

当系统的横向总阻尼与速度达到一定匹配程度时有可能出现无衰减振动(等幅振荡),随着输入速度条件的变化,等幅振荡能够还原成衰减振动,否则提高速度有可能出现发散振动,因而高速铁路开发过程中提出通过监测等幅振动来判断转向架横向稳定性[1,2]。我国提速及高速客车的出厂检验,横向稳定性的判别也是采用此标准。该标准是这样描述的:

(1)带通滤波器:0.5～10 Hz;

(2)连续振动6次以上的极限值为8～10 m/s2。

高速转向架技术在客车安全监测中是近年来不断引起重视的一个领域[2,3],我国近年来提出的客车安全监测标准[2],明确提出要进行转向架横向稳定性的状态监测。这一方面是出于安全的考虑,另一方面横向稳定性的监测可以起到“牵一发而动全身”的关键作用。众所周知,引起转向架横向失稳的第一要素是轮对踏面锥度,其他要素如转臂定位节点的刚度,抗蛇行减振器的性能等。而这些要素都会随着各种运用工况、运用里程的增加,使磨耗加剧,性能下降。因而通过监测横向稳定性亦可实现转向架的状态维修。

1 转向架横向失稳原理及评判标准

机车车辆是典型的非线性系统,其运动方程为˙X=f(x,˙x,…,v),当式中的速度确定以后,系统的稳定性也随之确定。稳定性的分析不仅是分析其零解的稳定性,还要研究全局稳定性。表征轮对和构架横向稳定性解的形式是相同的,都具有如图1的准等幅振荡的形式。

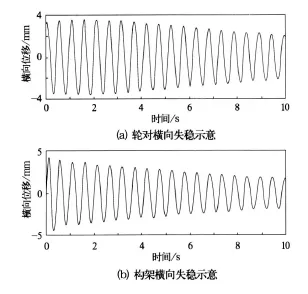
图1 轮对与构架失稳示意图

构架横向失稳时,自激振动是构架横向的主振型,其位移解的形式为[4]

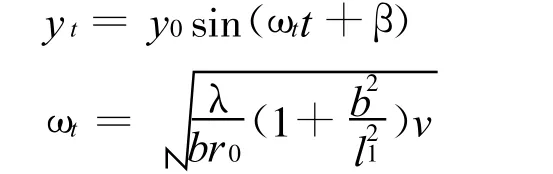
对于上述振动系统其加速度输出有如下近似关系

因而通过识别构架横向加速度即能识别转向架是否出现横向失稳。

2 构架横向加速度信号特点分析

构架横向振动加速度在不同运行工况下,表现出不同的信号特点。总体来讲,可以描述成频带丰富、随机性强、速度频带影响较突出的受迫振动特点。如图3是构架横向振动加速的时域信号和以某速度运行时的频域信号及相应的时频信号。

图2 速度170 km/h时构架横向加速度正常信号及低频10 Hz滤波结果

从图2可见,这种时变非平稳信号是构架横向运行时的常规状态。构架出现横向摆动,有近失稳的情况发生时由强迫振动的主振型转变成自激振动的主振型。因而要设计出的算法需满足在线实时监测的要求,同时还要满足随机受迫振动、一般自激振动、蛇行失稳振动3种振动状态监测的要求。如以230 km/h运动的车辆,若满足失稳监测的标准,当出现第6个振荡最后一个波形并完成振荡时,应在下一个振荡波形出现前,即第7个振荡波到来前完成监测算法的运算和报告。其相应的实时性要求指标如下:失稳频率为7 Hz,则1/7 s约运行9 m需要报告出蛇行失稳。这个数值是基于失稳标准报告的理论值。这样才能满足理论上的硬实时要求,可见高速运行车辆的稳定性监测实时性要求是非常关键的安全指标。

综上所述,转向架横向稳定性监测需要以半个波形持续的时间(最大时间长度为200 ms)为尺度来完成实时监测。因而,通过FFT频域寻找主频方法等基于时间帧的算法不能满足实时性要求。这里我们提出用半波长的信号能量与幅值标准作为特征参数,以高斯混合模型(GMM)为手段,按照UIC及铁标的标准通过DSP实现实时在线监测。

3 高斯混合模型的在线识别方法

3.1 高斯混合模型监测诊断过程

高斯混合模型是把概率密度函数表示成基函数的线性组合。有M个组元的混合模型可以表示成下式[5]:

这里参数P(j)称为混合系数;p(x|j)为组元密度函数,随着不同的组元而不同。模型为了表征概率密度函数其相应的约束条件为:

对于高斯分布的基函数,其协方差有不同的形式,每种表达方式中都含有3个参数:均值矢量 μ,维数为d,协方差矩阵 σ。协方差矩阵可以表示成任何正定d×d矩阵∑j,基函数表示成下式:

基于GMM的混合系统辨识问题可分为两大步骤进行:

(1)离线模型学习过程;

(2)在线模型应用以实现实时辨识。

3.2 基于EM算法的离线模型学习过程

通过EM算法根据下述步骤可估计出GMM参数。

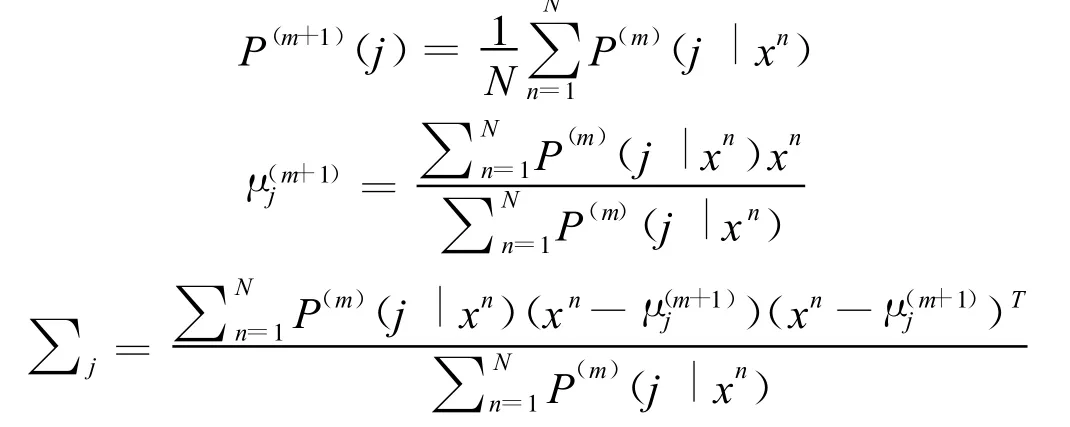
式中m为迭代次数;N是所有需要估计的数据点数。

3.3 在线监测模型的应用

在得到混合概率密度模型基础上,基于后验概率P(J|X),利用贝叶斯估计来进行状态估计(图3)。

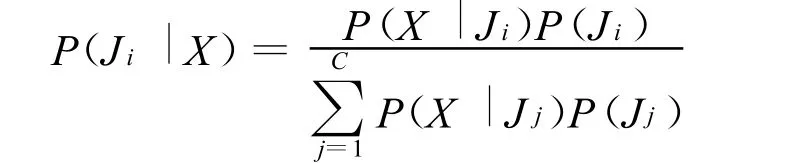
特征数据的采集及获取按照文献[6]利用 TCDS的转向架状态监测子系统实现。基于GMM的实时监测结果如图4。

图3 利用贝叶斯估计的155 km/h时速度波形

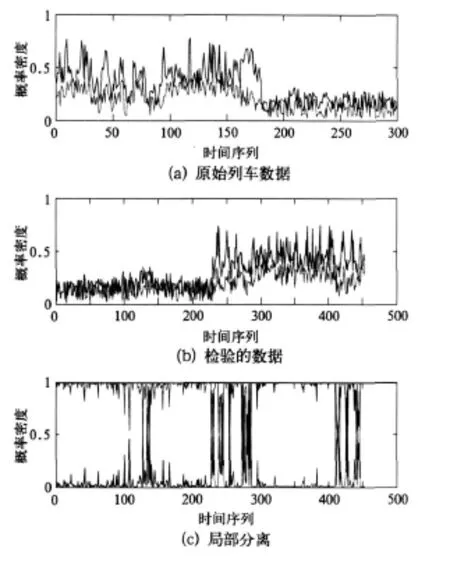
图4 基于GMM的实时监测结果

实时性分析:利用上述GMM方法,最长需要的帧数据长度为10 Hz滤波后的半个波长。假定系统采样频率为512 Hz,最大半波时间点数为107,对应为0.2 s。这样就能利用GMM从监测机理上实现0.3 s内诊断出转向架蛇行失稳,从而为实时监测构架横向稳定性奠定了理论基础(图5)。

图5 半波对应的时间点数

4 结束语

本文研究了利用高斯混合模型实现构架横向稳定性监测的机理及实现过程,通过KAX1客车安全监测诊断系统实现了横向稳定性的实时监测。分析表明300 ms内实现失稳判断是可能的,这样为更高速度如高速动车组的横向稳定性监测奠定了理论基础。

同时,本文的监测诊断结果也说明,运用25T型转向架横向稳定性时有出现不满足有关标准的情况,提示运用部门进行状态修时需要更加关注构架稳定性相关的检修维护单元,如轮对踏面锥度运用标准的维护、转臂定位节点的维护等。

[1] 曾敏士译.欧洲高速铁路联网高速列车技术条件[Z].铁道部标准计量所,1994.

[2] TB/T3188-2007.铁道客车行车安全监测诊断系统技术条件[S].

[3] 陈朝发,刘 峰,王旭如,等.客车行车安全监测诊断系统研究[J].铁道机车车辆,2003,23(S2):53-56,71.

[4] 王福天.车辆系统动力学[M].北京:中国铁道出版社,1994.

[5] Ian T.Nabney.NETLAB Algorithms for Pattern Recognition[Z].Springer,2002.

[6] 刘 峰.客车行车安全监测诊断系统研制工作报告,TY1569号[R].铁道科学研究院,2002.