基于变动频率滤波的新型数字锁相环

伍小杰,赵冰洁,符晓,戴鹏

(中国矿业大学 信电学院,江苏 徐州 221008)

1 引言

数字锁相环技术作为并网运行系统的关键技术之一,一直是人们研究的热点。为了使并网系统在各种非正常电网状态下仍然能够正常运行,单相电力锁相环在设计时应考虑频率变化、相角突变、电压跌落、电网谐波等各种非正常状态的影响。人们对单相 PLL的研究大多借鉴三相PLL[1]中的闭环结构,并通过构造2个虚拟的正交信号来实现。因此,单相PLL研究重点通常集中在鉴相器的设计上。文献[2]采用反Park变换法获得两路正交信号,但由于2个独立非线性环路的存在,使得采用传统的线性设计和分析方法很难准确获取系统参数。文献[3]提出的基于FIR滤波器实现的Hilbert变换法,随着滤波器阶数的升高,运算量增大,对控制器要求较高。

文献[4]提出了一种新颖的基于非线性动态模型的优化型数字锁相环(EPLL)。EPLL和其它PLL相比具有结构简单、灵敏度高、动态响应好的优点。针对传统EPLL抗谐波干扰能力差的问题,本文将变动频率平均值滤波(VFA)[5]的思想引入EPLL,在基本不影响其动态性能的条件下改善了EPLL的控制效果。

2 EPLL系统分析

EPLL控制结构如图1所示,采用误差闭环控制,由于EPLL的鉴相器可以实时地输出估算值和实际值的偏差,因此具有很好的动态响应性能。

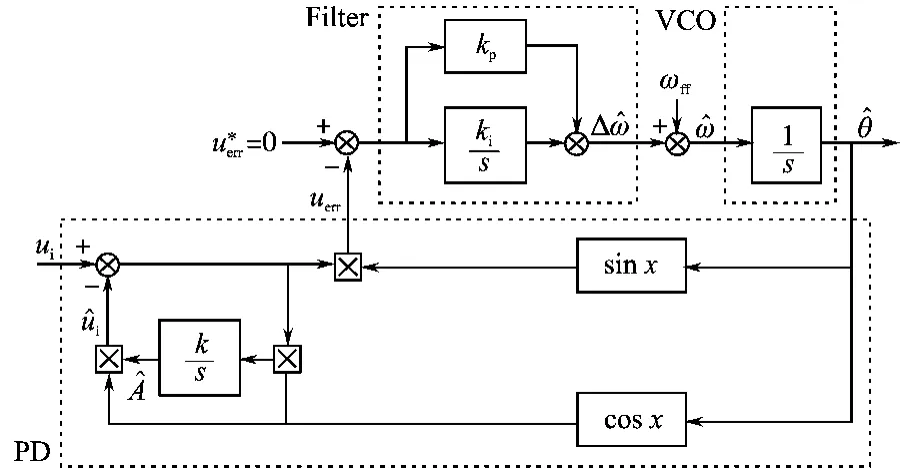
图1 EPLL系统结构框图Fig.1 Block diag ram of the EP LL system

但是当输入中ui含有谐波时,用表示输入电压第k次谐波的幅值,k=2n±1(n为正整数)为奇次谐波的次数。令=kωt+,为k次谐波的初始相角。,φ分别为输入和输出的初始相角。则鉴相器的输出在稳态下可以表示为

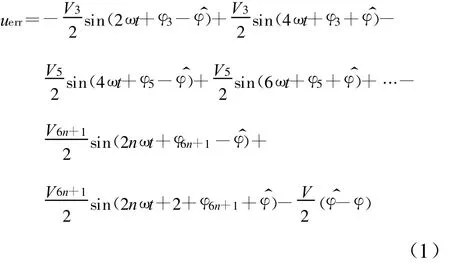
由式(1)可知,稳态下跟踪误差中仍然含有2,4,6等偶次谐波并导致EPLL输出相角的畸变,因此本文选择一种基于VFA原理的滤波器以兼顾锁相环对响应速度和系统计算量的要求,它结构简单易实现,对偶次谐波有较强的滤波效果,且对系统的响应速度影响较小。

3 VFA-EPLL系统构成

VFA-EPLL结构如图2所示。VFA滤波利用任何次谐波在一个基波周期内的积分为零的原理,通过一个变频延时环节滤除偶次谐波分量而完整保留直流分量,而在单相锁相环应用中,稳态下变频延时时间固定为0.02 s。

另外,针对文献[5]中EPLL在暂态过程中存在输出频率超调过大的问题又在主控制环路之外加入了斜率限幅和低通滤波器(LPF)。这样对主控制环路的动态性能影响不大,又有效减小了输出频率波动带来的影响。

在实际系统的上电瞬间,电网瞬时角度是无法预测的。考虑极限当-φ=180°时,仿真分析的稳态时间约为2个电网周期。因此,本文借鉴了传统过零检测的思想,将初始相角定位在0°附近,从而使调节时间缩短至一个电网周期以内。

图2 改进后的VFA-EPLL结构框图Fig.2 Block diagram of the improved VFA-EPLL system

4 仿真研究

在Matlab软件上对所提方法进行仿真。仿真条件:电网频率50 Hz,电网电压220 V,调节系数m=1.2,采样频率=5 kHz,滤波器截止频率f=25 Hz,斜率限幅di/dt=12。

公用电网允许的电压谐波总畸变率为5%,图3是0.22 s加入40%3次谐波的仿真结果,其中是鉴相器输出信号。通过对比可以发现,3次谐波导致传统的EPLL锁相失败。而正弦波输出验证了VFA-EPLL对谐波的抑制作用。

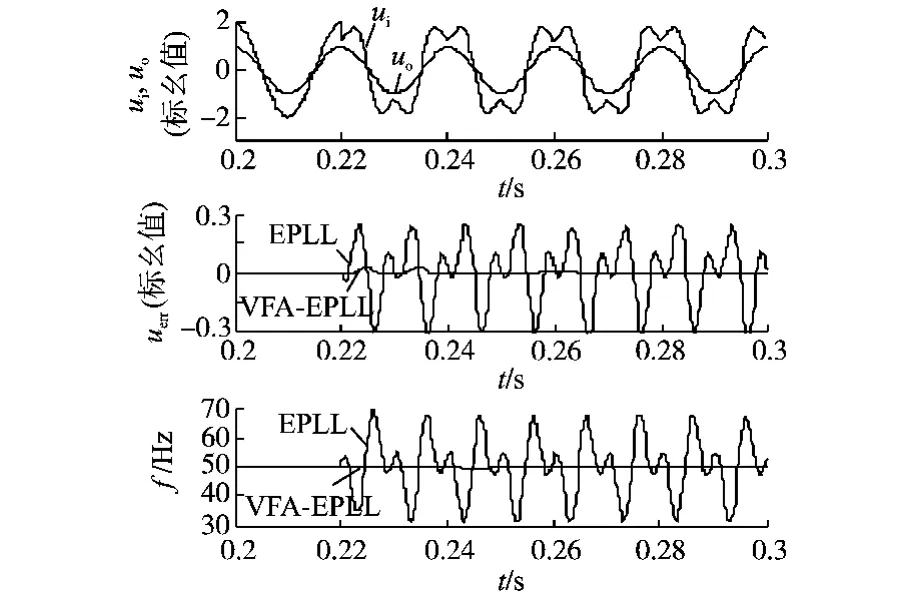
图3 输入含谐波时PLL稳态输出Fig.3 The P LL waveforms in the steady states when the harmonic is inserted

图4是电网初相角为180°的仿真结果。该结果表明,当加入了初始相位角定位控制后,调节时间由原来的2个电网周期缩短为0.5个周期。

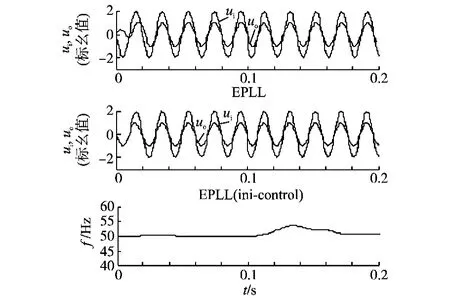
图4 初始相角和频率变化波形Fig.4 The waveforms when initial phase angle and frequency change

考虑电网频率在50±1 Hz范围变化,在0.1 s将频率升至51 Hz,由图4可知大约1个周期后相位重新被锁定,而频率则在3个周期后以较小超调过渡至51 Hz,这证明了改进EPLL的优越性:既不影响主环路的动态性能,又有效地减小了频率的波动。

图5是电网相位角在0.22 s突加40°的仿真结果。由图5可以看出,由于频率处理模块在主控制环路之外,因此虽然频率响应的动态性能不高,但相位角的重新锁定仍只需1个电网周期。

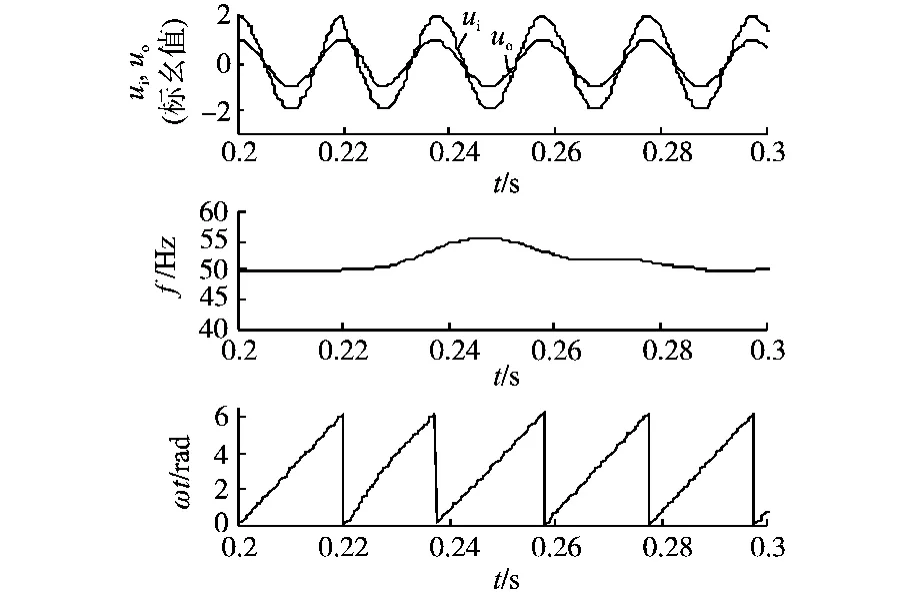
图5 相位角突变40°时波形Fig.5 The waveforms of a phase-angle jump of 40°

电网电压通常允许在 90%～110%之间变化,图6是电压在0.22 s由100%→70%变化的仿真结果,该仿真结果表明,电压幅值的变化并不影响PLL对输入的跟踪锁定。这是由于在稳态情况下,相角误差信号uerr近似为零,此时估算电压幅值A＾跟随输入电压幅值V而改变,并不影响鉴相器的输出。

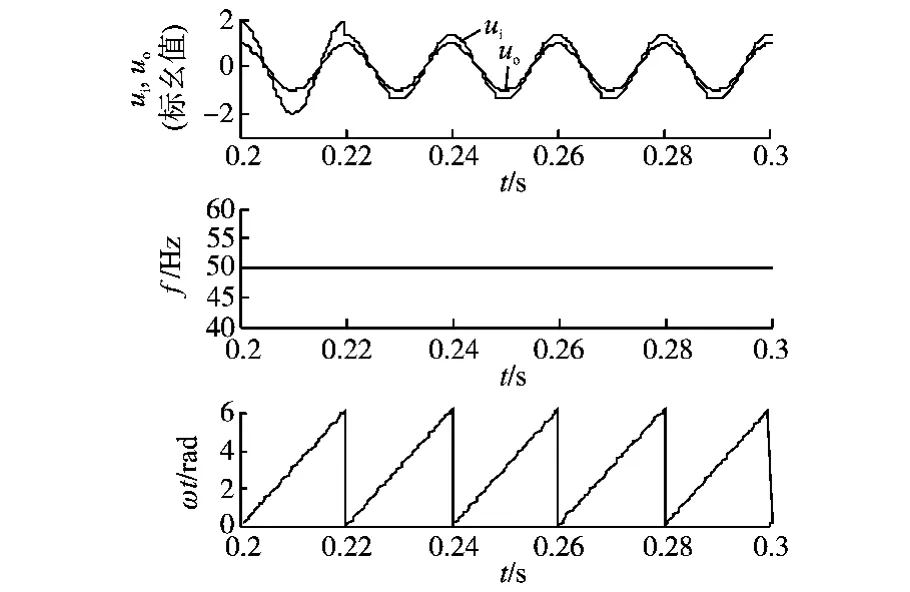
图6 电压幅值100%→70%变化波形Fig.6 The waveforms of the voltage changes from 100%to 70%

5 实验验证

搭建了以数字信号处理器TMS320F2812为核心的实验装置,利用dSPACE实时仿真平台中配有的I/O板DS2103(D/A转换)实现任意电压波形的产生,并将DSP A/D采样得到的输入信号和运算得到的锁相环输出信号通过SPI模块控制T LV5614DAC芯片输出。实验参数选择和仿真参数相同。

图7a是输入为标准正弦波时,输入电压和锁相环输出角频率 ωt的实测波形。可见ui和ωt过零点相同,输入输出同相位,实现了PLL对输入的跟踪锁定。图7b是输入信号中加入20%3次谐波和10%5次谐波时PLL的稳态响应波形。对比图7a和图7b可见谐波电压并没有影响PLL的正常跟踪锁定性能,从而验证了提出的改进EPLL的优越性。

图7 VFA-EP LL实验波形Fig.7 Experimental waveforms of VFA-PLL control

6 结论

在对现有EPLL的性能进行分析的前提下,引入VFA滤波器消除谐波干扰下相角锁定的稳态误差。在主控制回路之外加入频率的滤波和斜率控制,并将此输出频率作为VFA滤波器的时间常数。借鉴硬件过零检测的思想,在估算的零点附近使能锁相环并设置相应的初始状态,给出仿真结果和实验结果。

仿真和实验结果分析表明,本文所提出的VFA-EPLL解决了其存在的抗谐波干扰能力差的问题;减小了暂态下频率的波动;缩短了相角锁定的调节时间,解决了初始相角偏差过大可能引起的失锁问题。

将VFA思想引入EPLL来改进其控制性能是本文新的尝试,并在此基础上解决了频率超调过大、初始相位角定位不准等问题。不足之处在于频率控制模块导致相角锁定先于频率锁定,影响了频率响应速度。

[1] 孔雪娟,罗昉,彭力,等.基于周期控制的逆变器全数字锁相环的实现和参数设计[J].中国电机工程学报,2007,27(1):60-64.

[2] Arruda Lícia N,Silva Sidelmo M,Filho B J C,et al.PLL Structures for Utility Connected Systems[C]∥36th Industry Applications Society Annual Meeting,2001,4:2655-2660.

[3] 任碧莹,钟彦儒,孙向东,等.基于有限冲击响应滤波器线性相移控制的单相系统数字锁相环[J].电工技术学报,2008,23(8):121-125.

[4] Rubens M,Santos Filho,Paulo F Seixas,et al.Comparison of T hree Single-phase PLL Algorithms for UPS Applications[J].IEEE T ransactions on Power Electronics,2008,55(8):2923-2932.

[5] Sybille G,Le Huy H.Digital Simulation of Power Sy stems and Power Electronics Using the Matlab/Simulink Power System Blockset[C]∥IEEE Power Eng Soc Winter Meeting,2000:2973-2982.

修改稿日期:2010-05-24