基于重复控制的抑制电机周期性负载扰动的方法

李锐,黄文新,储剑波

(南京航空航天大学 航空电源航空科技重点实验室,江苏 南京 210016)

在一些电机驱动应用场合,所带负载是一种周期性的扰动负载,比如空调压缩机。当单转子压缩机低速运转时,转矩会产生周期性的变化,这样会引起转速的波动,当转速波动较大时,空调压缩机抖动较大,对空调管路有一定的危害。因此,提升空调压缩机的低频运转性能是高性能变频空调必须要解决的问题。重复控制器是日本的Inoue于1981年首次提出的,用于伺服系统重复轨迹的高精度控制;它是根据内部模型原理和周期性参考信号的特点,将产生参考输出信号的“模型”置于稳定的闭环系统内,从而实现对周期性参考信号或周期性的外部干扰信号的稳态跟踪。本文中把它用在速度环上,用来抑制压缩机周期性的扰动负载,减小压缩机的转速抖动。

1 重复控制器的分析

理想的重复控制系统框图如图1所示,但是这种结构的重复控制器的稳定性完全取决于G(z)的参数,系统很敏感,极其容易受到干扰而进入到不稳定的区域。

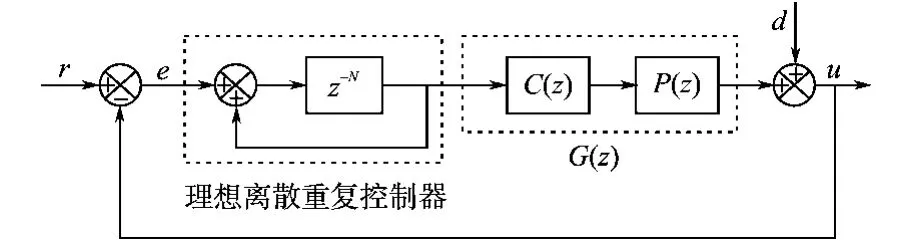
图1 理想重复控制器框图Fig.1 The block diagram of ideal repetitive controller

在实际中应用的重复控制器均引入了相应的补偿参数来改造G(z)从而提高系统的稳定性。本文采用了插入式重复控制器,其特点是:原始控制器的设计和重复控制器的设计相互独立,对于一个没有采用重复控制器的系统,不必对原始系统进行任何修改,仅需要增加一个相加环节,就可以将重复控制器“插入”到原始系统中,从而抑制系统的周期性扰动。加入补偿后的重复控制器框图如图2所示。

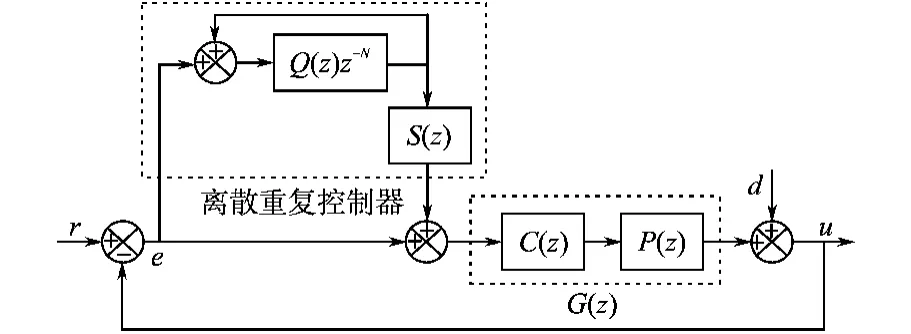
图2 重复控制器框图Fig.2 The block diagram of repetitive controller

图2中,r为系统的输入;u为系统的输出;e为误差信号;d为干扰信号;Q(z)为低通滤波器;S(z)为补偿器;N为每基波周期对扰动的采样次数,N=/f(f为扰动基波频率,为采样频率);z-N为周期延迟环节。

若要系统稳定,要满足下面2个条件:

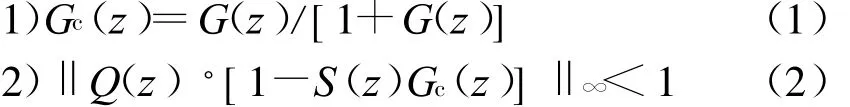
对于图2所示的重复控制系统,求得系统的误差传递函数为

低通滤波器的选择需要考虑2个方面,即保证稳定性和提高系统的精度。具体而言,在低频段,Q(z)应尽量接近于1,使得在这一频段内具有重复频率信号的误差充分衰减,以保证系统对重复性扰动的抑制作用;在高频段,Q(z)应迅速衰减到远小于1以保证系统的稳定性。Q(z)一般取二阶巴特沃斯滤波器,形式为

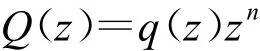
式中:q(z)为二阶巴特沃斯滤波器;zn用以补偿二阶巴特沃思滤波器的相位,使得∠q(z)zn≈0。

S(z)的设计要考虑到(z)的相位和幅值,即对(z)的相位和幅值都进行补偿;S(z)一般选择形式为

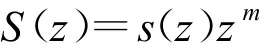
式中:s(z)为低通滤波器,滤波器的阶数与(z)的表达式有关;zm用以补偿(z)◦s(z)的相位,使得∠Gc(z)s(z)zm≈0。

引入相位补偿后的重复控制器的框图见图3。

图3 引入相位补偿后的重复控制器的框图Fig.3 The block diagram of repetitive controller after phase compensation

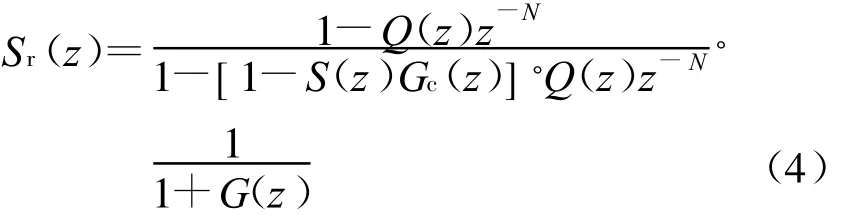
定义系统的灵敏度函数为S0(z)=1/[1+G(z)]为没加重复控制器的系统灵敏度函数;系统灵敏度函数反应了对系统扰动的抑制能力。由式(4)可知,在低频时,Q(z)≈1,Sr(z)≈0,由式(3)可知e≈0,系统的输出能够很好地跟踪输入。

2 重复控制器的设计

空调压缩机的参数为:定子电阻1.4 Ω;d轴电感 5.6 mH;摩擦系数 0.001;q轴电感9.1 mH;主极磁通 0.067 Wb;极对数2;转动惯量0.842×10-4kg◦m2。

不加重复控制器时,在时域内电机系统等效的闭环传递函数Gc(s)为

Gc(z)为Gc(s)的z变换,采样频率为10 kHz。由于Gc(z)在低频段的幅值一直为1,所以s(z)可以取1,zm=z5。图4与图5为Gc(z)和Gc(z)zm的相频特性。由图5可知,相位补偿后,(z)在低频段的相位接近于0。

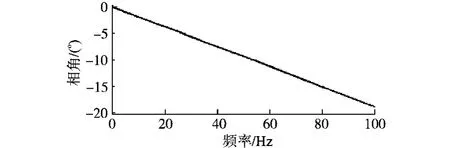
图4 Gc(z)的相频特性Fig.4 Phase-frequency characteristic of Gc(z)

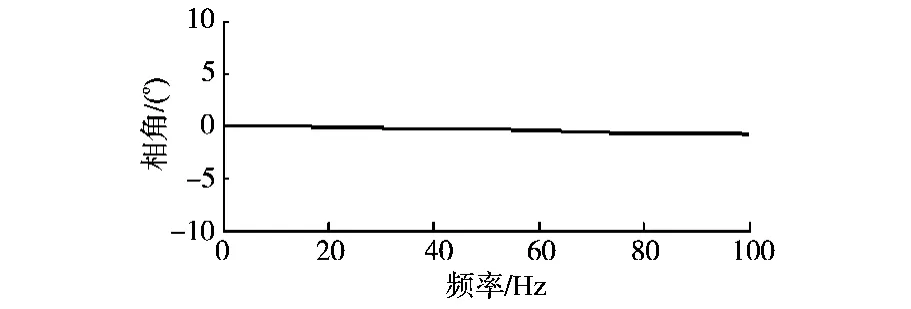
图5 Gc(z)zm的相频特性Fig.5 Phase-frequency characteristic of Gc(z)zm

低通滤波器选截止频率为150 Hz的二阶巴特沃斯滤波器,在时域内,

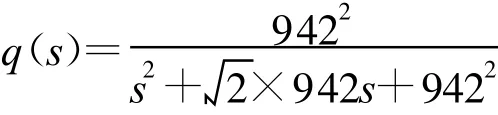
q(z)为q(s)的z变换,采样频率为10 kHz,zn=z16。图 6与图7为q(z)和q(z)zn的相频特性。

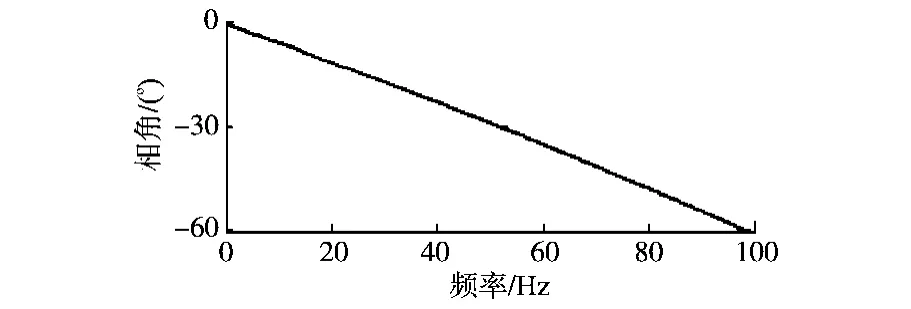
图6 q(z)的相频特性Fig.6 Phase-frequency characteristic of q(z)

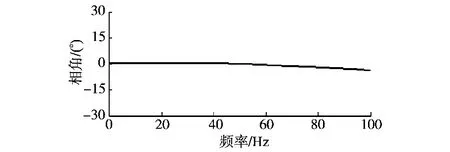
图7 q(z)zn的相频特性Fig.7 Phase-frequency characteristic of q(z)zn

由图7可知,相位补偿后,Q(z)在低频段的相位接近于0。

3 系统仿真和实验

按照上述参数设计,引入重复控制器后,电机闭环控制的系统框图如图8所示。驱动压缩机的永磁同步电机的控制方案采用id=0的矢量控制方案,包括速度环、电流环、逆变器、SVM、速度估算模块等。由于压缩机内部处于密封状态,工作环境恶劣,并且充满了腐蚀性的高压制冷剂,无法安装位置传感器,所以本文采用的是估算转子的转速。电机参数在第2部分已给出,直流环节电压为310 V。仿真采用的是Matlab软件,实验是基于Freescale公司的56F8037控制芯片的硬件平台。

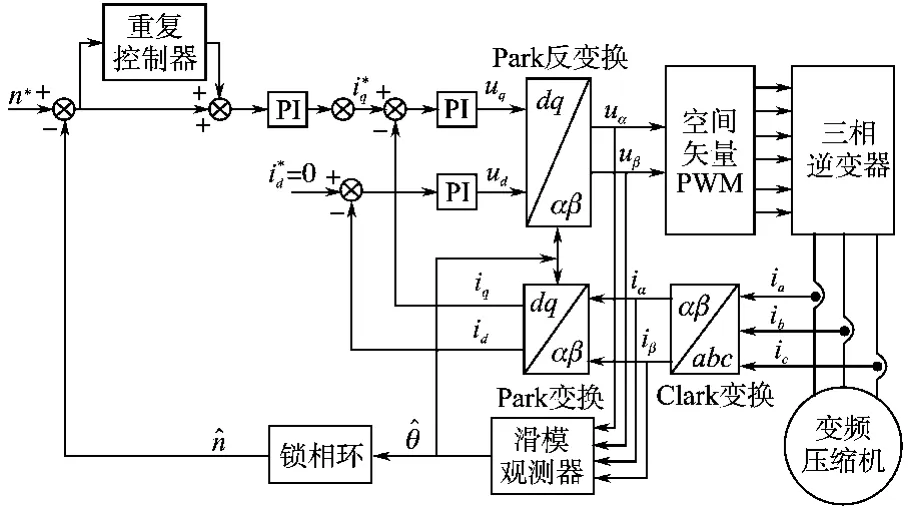
图8 系统控制框图Fig.8 Block diag ram of control system

由于压缩机的扰动频率与转速有关,扰动频率就是压缩机的机械频率;所以当压缩机的转速没有稳定时,扰动频率也不是定值,负载扰动不是周期性的,此时重复控制器对扰动没有抑制能力,故不让重复控制器起作用;当压缩机的转速稳定后,再让重复控制器起作用;此处的扰动负载用图9所示的波形来模拟,电机在600 r/min时的仿真和实验结果如下。

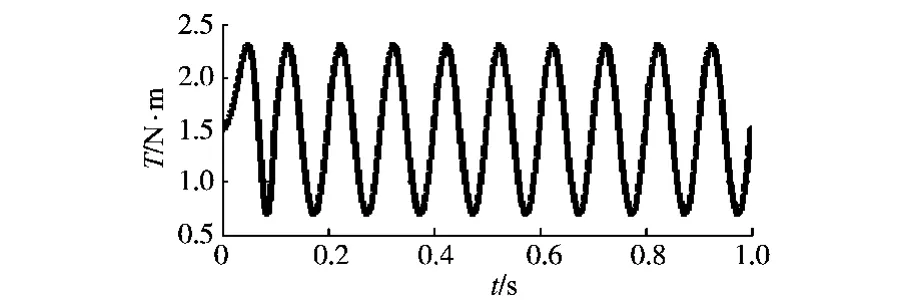
图9 压缩机的模拟扰动负载Fig.9 T he analog disturbance load of compressor

从仿真波形图10中可以看出,加入重复控制器后,压缩机的转速波动明显减小了。

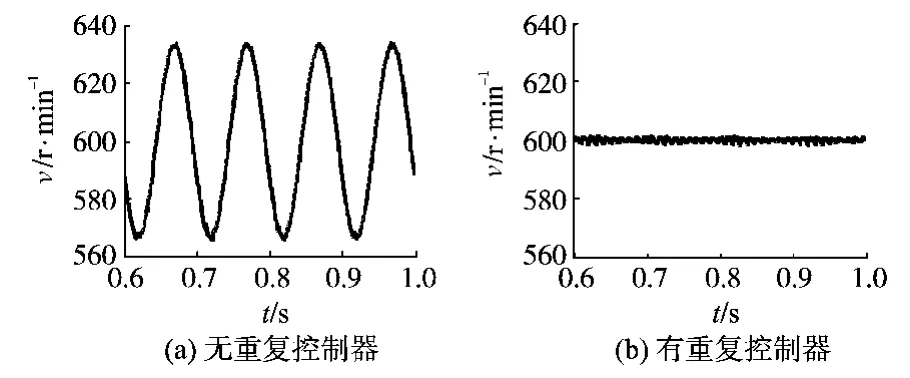
图10 有、无重复控制器时压缩机的转速Fig.10 The velocity of compressor without and with repetitive controller

由于重复控制器只是加在转速闭环上,所以对电流没有影响,从仿真波形图11中可以看出,加入重复控制器后,压缩机的电流没有变化。

从实验波形图12中可以看出,加入重复控制器后,压缩机电流波形基本没有变化;图13中电机的转速扰动明显减小,与仿真结果一致。

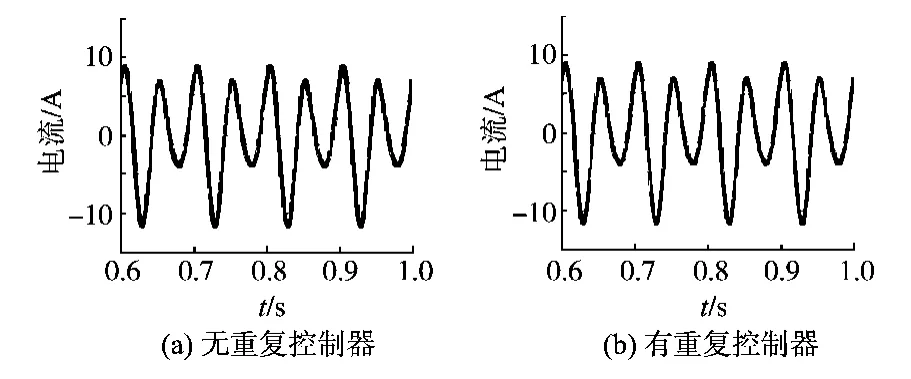
图11 有、无重复控制器时压缩机的 A相电流Fig.11 The A-phase current of the compressor without and with repetitive controller

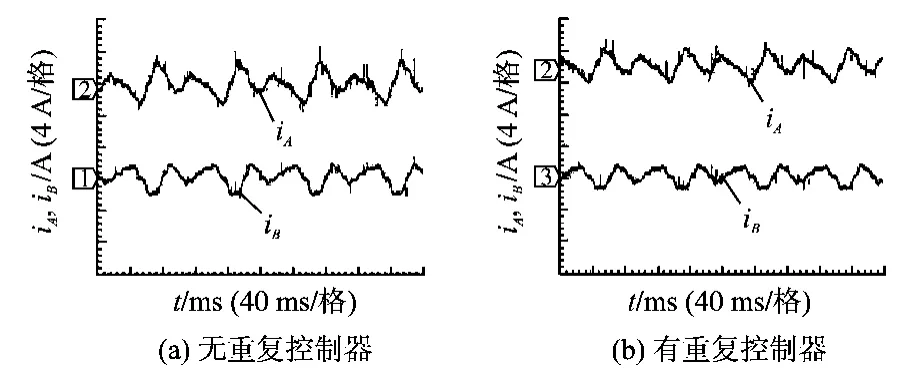
图12 有、无重复控制器时压缩机的电流波形Fig.12 T he current of compressor without and with repetitive controller

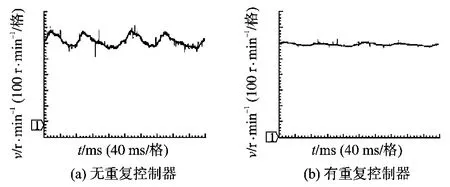
图13 有、无重复控制器时的压缩机转速Fig.13 T he velocity of compressor without and with repetitive controller

4 结论

由仿真和实验结果可以看出,当系统有周期性扰动时,若不加重复控制器,系统输出转速抖动较大,若引入重复控制器,系统输出转速抖动较小。这说明重复控制器对周期性的扰动具有很好的抑制作用,仿真和实验结果与理论分析一致。重复控制器采用的是插入式,在不改变原来控制系统的基础上,直接加入重复控制器,就可以明显地抑制系统转速的抖动,设计简单,为工程实践和设备改造提供了一种良好的借鉴。

[1] Mi-Ching Tsai,Wu-sung Yao.Design of a Plug-in Type Repetitive Controller for Periodic Inputs[J].IEEE Transactions on Control System Technology,2002,10(4):547-555.

[2] 彭宏刚,于豫民,张敏华 .基于插入式重复控制器的摆动扫描控制系统研究[J].航天返回与遥感,2008,29(3):51-56.

[3] Wu-sung Yao,Mi-Ching.Analysis and Estimation of Tracking Errors of Plug-in Type Repetitive ControllerSystems[J].IEEE Transactions on Automatic Control,2005,50(8):1190-1195.

[4] 游志青.基于重复控制技术的数字式逆变器电源的研究[D].南京:南京航空航天大学,2003.

[5] 储剑波,胡育文,黄文新,等.一种抑制永磁同步电机转速脉动的方法[J].电工技术学报,2009,24(12):43-49.

修改稿日期:2010-06-19