卫星导航接收机延迟锁定环鉴相器有限字长分析*
刘小汇,李峥嵘,欧 钢
(国防科技大学电子科学与工程学院,湖南长沙410073)
卫星导航接收机在跟踪阶段对扩频码的跟踪,将影响测距和定位精度以及电文解调的误码率,通常使用延迟锁定环(Delay-Locked Loop,DLL)完成伪码跟踪[1]。延迟锁定环由环路鉴相器和环路滤波器、数控振荡器(Numerically Controlled Oscillator,NCO)组成[2]。其中环路鉴相器利用预检测积分器输出的相关结果,计算输入相关信号中的码延迟相位,进而估计得到本地码相位与接收码相位的偏差,误差用以调整本地码生成器,完成对接收伪码的精确跟踪。环路鉴相器是DLL的重要组成部分,它直接决定了码环的跟踪精度,根据鉴相器是否需要载波信息,将延迟锁定环分为相干延迟锁定环和非相干延迟锁定环[3]。
一般的非相干延迟锁定环鉴相器有点积(Dot Product,DP)鉴相器、早迟功率(Early Minus Late Power,EMLP)鉴相器、早迟幅度(Early Minus Late Amplitude,EMLA)鉴相器和归一化的早迟幅度(unified EMLA)[3]鉴相器。其中归一化的早迟幅度鉴相器,去除了DLL环路对信号幅度的敏感性,能有效改善在脉冲干扰等情况下的接收性能[3]。
由于鉴相器对延迟锁定环的性能具有重要影响,因此如何提高其输出的码延迟精度,是许多学者研究的内容[4-6]。然而除了算法本身性能外,在使用数字信号处理器实现由无限精度向有限精度转换时,引入的精度损失是否可以忽略?鉴相器的有限字长问题包括系统输出有限字长、运算过程的有限字长、输入数据有限字长等。前两种情况,系统输出字长影响相对单一,易于分析;运算过程有限字长问题,由于与具体的运算方法紧密相关,多数的文献均假设有足够的长度表示数据高位和低位,使得计算过程没有溢出,由舍入操作产生的局部量化误差功率远小于输入数据的量化噪声功率[7]。对于输入数据的有限字长问题,Widrow建立了目前通用的字长分析噪声模型[8]:系统输入的有限字长信号可以看成全精度信号与随机噪声的叠加,字长误差(或噪声)是与信号本身完全不相关的白噪声,字长误差在线性系统中具有线性叠加特性。这种假设使得线性系统有限字长的问题易于分解为信号与噪声的叠加,已使其得到了很好的解决。而对于如鉴相器般的非线性系统,由于字长误差在非线性系统中不再具有叠加特性,且误差有可能反馈至输入端,使得线性系统的分析方法将不再适用。对于延迟锁定环路中鉴相器的有限字长效应的研究,文献[9]分析了鉴相器输出的有限字长与伪距精度损失的关系,由于假设输出量化噪声与鉴相器的热噪声不相关,因此总的噪声为热噪声与量化噪声的叠加,使得分析难度大大降低。然而对于输入信号有限字长,其量化噪声在非线性计算的鉴相器中不能简单叠加得到输出噪声,因此分析难度大,目前还未有文献对此进行报道。
本文将以常用的归一化早迟幅度鉴相器为例,分析延迟锁定环鉴相器的输入信号有限字长对输出性能的影响,其余类型鉴相器的分析方法类似。
1 误差建模与统计特性分析
1.1 字长误差模型
图1为鉴相器的字长误差模型,由于硬件实现的局限性,常对输入鉴相器的相关累加和信号与输出鉴相器的相位值进行舍入,鉴相器噪声由鉴相输出的噪声nPD和量化噪声组成。量化噪声可以分为输入信号的量化噪声ne1和输出相位的量化噪声ne2。对于输出相位的量化噪声,可认为量化误差是平稳随机序列并且与输出相位不相关,因此对总噪声的影响可以采取直接累加的方法;对于输入信号的舍入量化噪声ne1,因为鉴相操作是一个非线性的过程,对鉴相器噪声的影响不能简单地累加。假设输入信号的字长为b1,则鉴相器输出方差是b1的非线性函数,同理假设输出相位的字长为b2,则鉴相器在舍入量化效应下总的输出噪声为:
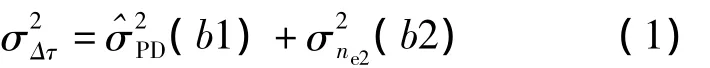
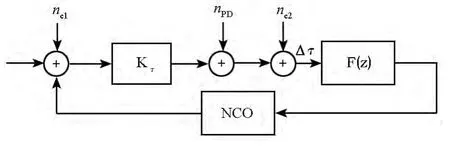
图1 鉴相器的字长误差模型Fig.1 Error model of word-length effect for code discriminator
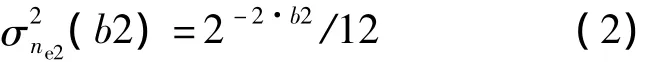
1.2 输入信号的有限字长效应分析
为了计算输入信号在b1位字长下鉴相器输出噪声,首先分析输入信号量化后的统计特性。不考虑伪码相位跟踪误差,在中频信号经过解调、积分清零器后的相关累加值I、Q信号可以分别写成[11]:
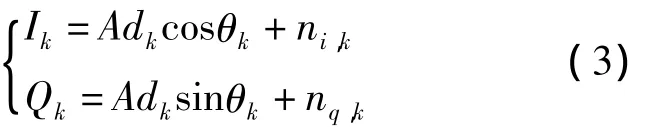
式中:A为信号幅度;dk为调制的导航电文;θk为残留的载波相位误差;ni,k和nq,k为噪声且相互独立,方差均为σ2。相关累加值Ik、Qk的联合概率密度函数为[12]:
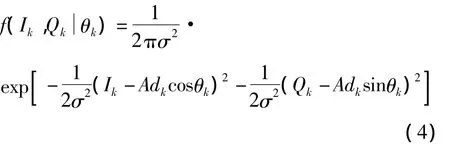
对I、Q信号进行b1 bit舍入量化,等效于引入了一个均匀等概率分布的白噪声,分别记为eI和eQ。则输入信号舍入量化后的表达式为:
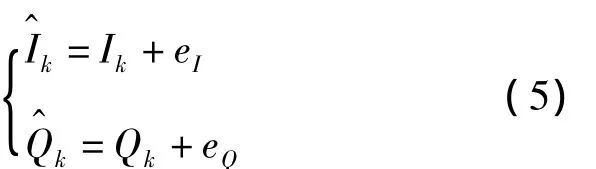
可知量化噪声eI和eQ的概率密度、均值和方差分别为有效位远大于舍入位数时),量化间隔为q=2-b1。
由I、Q的联合概率密度表达式(4)可知I、Q的概率密度分别为:
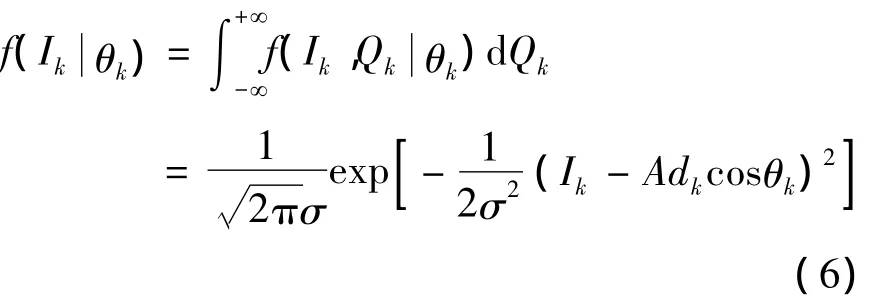
同理:
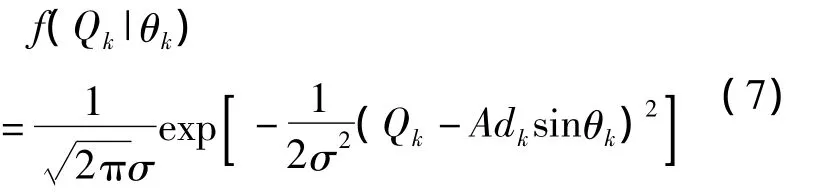
显然I、Q为相互独立的随机变量。假设舍入误差eI与信号Ik不相关,其联合概率密度为:
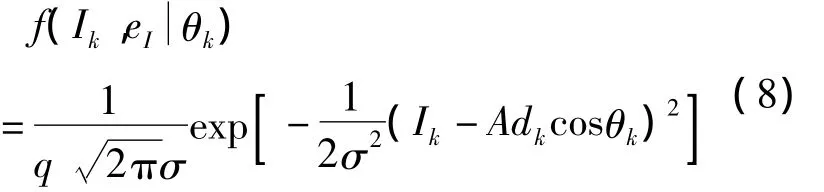
同理,eQ与Qk的联合概率密度为:
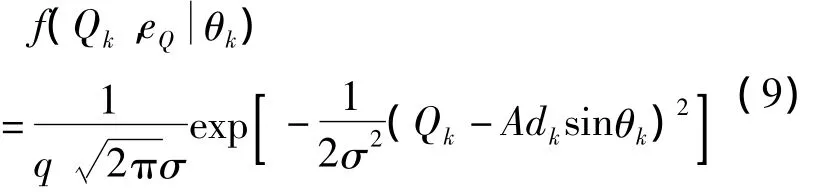
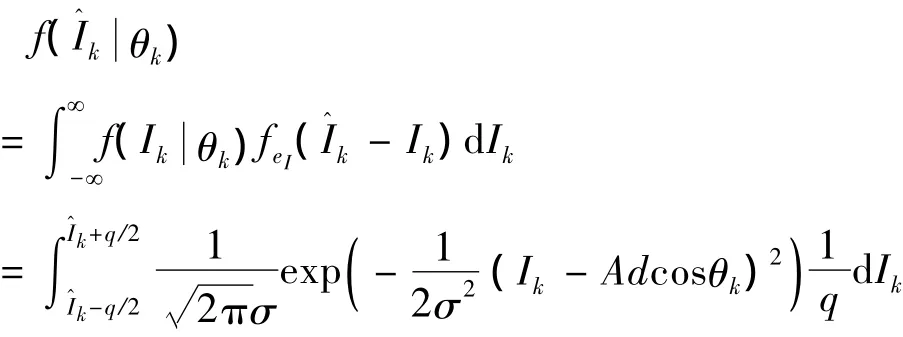
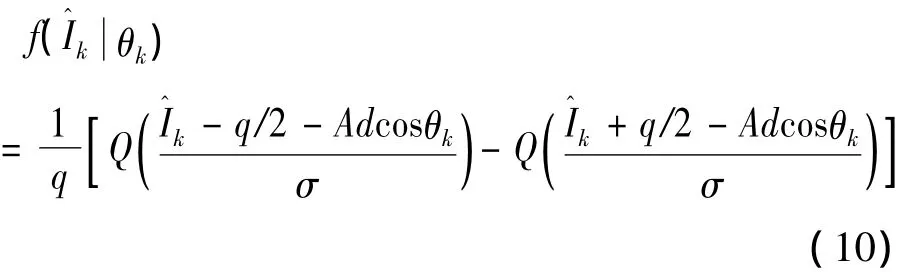
同理可以求出的概率密度:
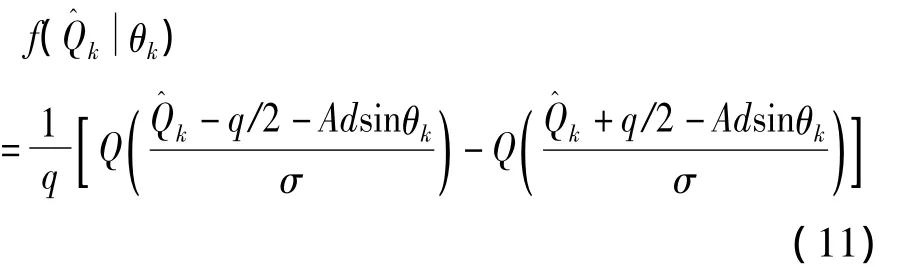
1.3 鉴相器的统计特性
归一化早迟幅度鉴相器的表达式为:
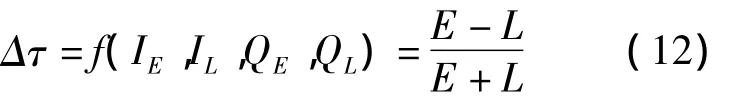
式中,Δτ为输出的码片误差E,L分别为超前、滞后相关器输出的包络值,超前、滞后间隔的码片数d一般取值0.5个码片。由上一节已知相关输出信号I、Q为正(余)弦信号加上高斯白噪声,则I、Q的包络值E、L服从莱斯分布(Rice distribution),于是超前、滞后包络E、L的概率密度为:

其中:I0(·)为0阶第一类贝赛尔函数,且x〉0;α2/2σ2为输入信号的信噪比,σ2为输入噪声的方差。由E、L的概率密度,可以计算出随机变量Z=L/E的概率密度为:
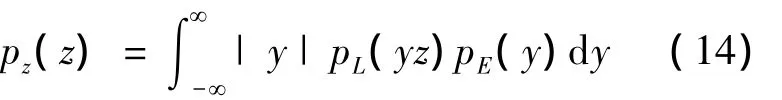
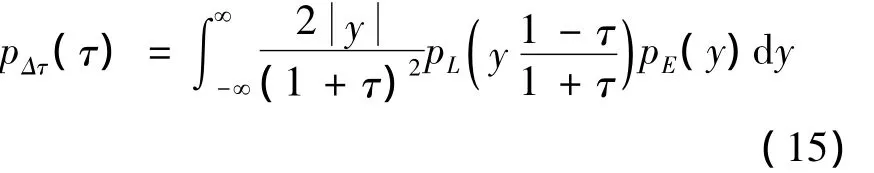
于是全精度下的鉴别器输出的均值和方差分别为:
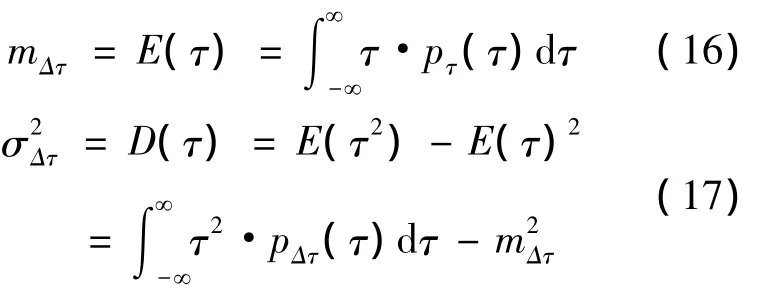
对输入鉴相器的信号I、Q进行有限字长的量化后,设分别为量化后早、迟码的包络,由上一节可知超前支路输入信号IE量化后的概率密度函数为:
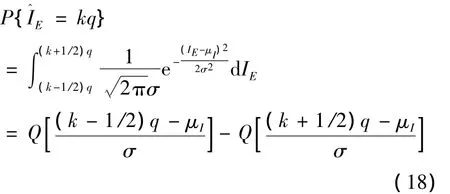
式中,q为量化间隔,μI为信号均值,σ为噪声方差。同理QE量化后的概率密度函数为:

于是量化后的早码包络的概率密度为:
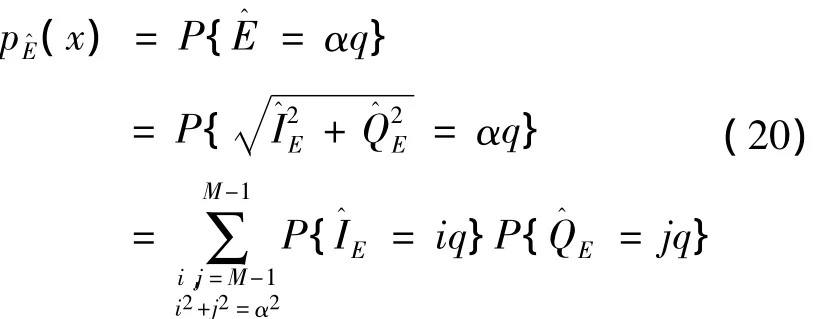
在离散的点…,±(M-1))上取值。量化后迟码的包络可以同理求得:


其中k=i/j为非整数,有种组合的取值k(1),k(2),…,k(w),于是量化后鉴相器输出的码相位的均值和方差为:
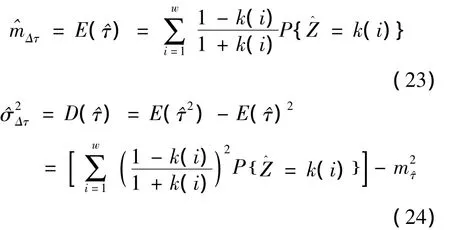
式(23)和式(24)显示了输入信号有限字长对鉴相器输出均值和方差的影响。
2 鉴相器性能分析
2.1 字长效应对鉴相器方差的影响
图2为相关输出信号信噪比为8~18dB时,在不同量化条件下,鉴相器输出的方差理论计算与仿真结果的对比。由图可知,理论分析与仿真结果基本吻合,输入鉴相器的信号进行4bit及以上的量化时,其输出码相位方差与全精度相比差别不大。
2.2 字长效应对环路性能分析及仿真验证
鉴相器对延迟锁定环环路伪码相位精度的影响为[13]:
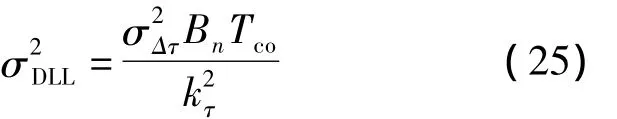
式中,Bn为环路的等效噪声带宽,kτ为鉴相器的增益,Tco为鉴相器的相干积分时间。由于文献[9]已经分析了鉴相器输出字长对伪码精度损失的影响,本文将忽略这一影响,将输出量化噪声设置为0。因此可以定义伪码相位精度损失为输入有限字长的环路跟踪误差与全精度下的跟踪误差之比[14]:
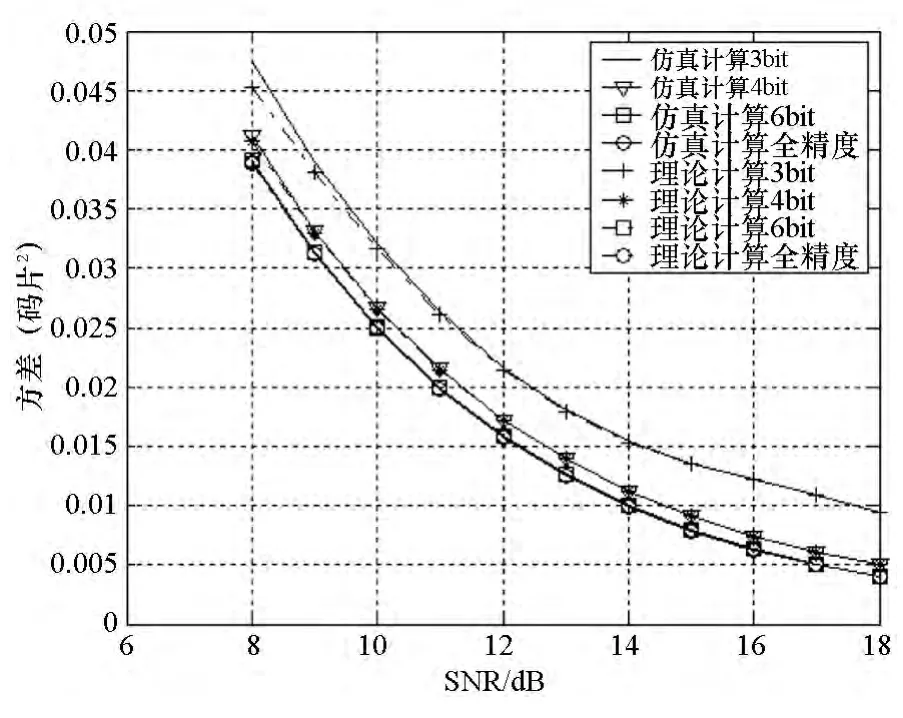
图2 不同量化条件下的方差Fig.2 Discriminator's variance caused by different quantization
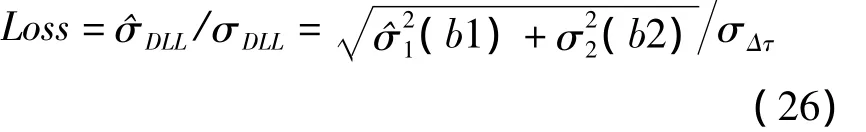
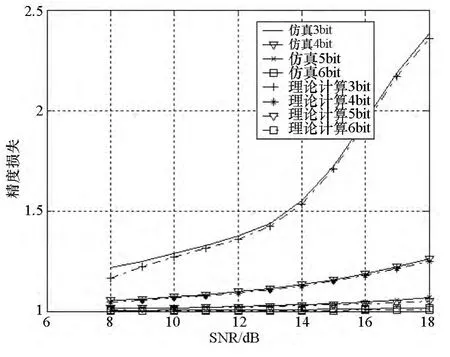
图3 不同量化下的伪距精度损失Fig.3 Pseudo-range accuracy loss caused by different quantization
图3为输入信号在3,4,5,6bit量化下,相干积分时间为1ms,环路带宽为2Hz,鉴相增益为1,采用GPS的C/A码时,理论计算与仿真实验的伪码精度损失情况对比。从图中可以看出,在低信噪比下,不同量化造成的精度损失差别不明显,因为这时是信号中的白噪声占主导。然而随着信噪比的增加,量化噪声将超过信号中的白噪声,由量化导致的精度损失将有明显区别。另外,随着输入信号信噪比的增大,精度损失将增大,但对于4bit及以上量化,随着信噪比的增加,其损失增加并不明显,如信噪比18dB时,5bit量化带来的精度损失为1.05(0.2dB),忽略动态应力等其他测量误差,与全精度下的伪距测量值相差0.029 3m;6bit量化带来的精度损失为1.005(0.02dB),与全精度测量下的伪距测量值相差0.011m,输入信号有限字长带来的伪码精度损失将可以忽略。
3 结论
通过对鉴相器字长误差的建模,分析了输入信号有限字长下的鉴相器输出误差以及字长对环路伪码跟踪精度的影响。理论推导与仿真实验结果表明:对于归一化早迟幅度鉴相器,输入信号有限字长越大对输出误差影响越小;输入信号字长对环路伪码跟踪精度亦有影响,在输入信号高信噪比下尤为明显,随着输入信号信噪比的增加,伪码精度损失将增加;而当输入信号采用4bit及以上量化时,即使信噪比增大,由量化带来的伪码跟踪精度损失也可忽略。以上结论能为基于软件无线电的定点数字信号处理接收机的设计提供参考。
References)
[1]Juang J C,Chen Y H,Kao T L,et al.Design and implementation of an adaptive code discriminator in a DSP/FPGA-based Galileo receiver[J].GPS Solution,2010,14(3):255-266.
[2]Parkison B W.Global position system:theory and applications[M].USA:American Institute of Aeronautics and Astronautics,1996.
[3]Kaplan E D.Understanding GPS principles and applications[M].USA:Artech House,1996.
[4]Ma L,Wang S C,Liu Z G,et al.Design and analysis of two new DLL discriminator algorithms[C]//Proceedings of International Conference on Mechatronic Science,Electric Engineering and Computer,2011:961-965.
[5]Borio D,Fantino M,Presti L L,et al.Robust DLL discrimination functions normalization in GNSS receivers[C]//Proceedings of IEEE/ION Position,Location and Navigation Symposium,2008:173-180.
[6]Liu L Y,Amin M G.Multipath and pre-correlation filtering effect on GPS noncoherent early-minus-late power discriminators[C]//Proceedings of the 5th IEEE International Symposium on Signal Processing and Information Technology,2005:417-422.
[7]Keding H,Willems M,Coors M,et al.FRIDGE:a fixedpoint design and simulation environment[C]//Proceedings of Design,Automation and Test in Europe,1998:429-435.
[8]Winrow B.Statistical analysis of amplitude quantized sampleddata system[J].Transaction of American Institute of Electrical Engineers,Part II:Applications and Industry,1960,79(6):555-568.
[9]刘峰,李欣,龙腾.卫星导航接收机定点环路跟踪精度研究[J].北京理工大学学报,2010,30(6):707-712.LIU Feng,LI Xin,LONG Teng.Research on the tracking accuracy of fixed-point loop for satellite navigation receiver[J].Journal of Beijing Institute of Technology,2010,30(6):707-712.(in Chinese)
[10]Oppenheim A V,Schafer R W,Buck J R.Discrete-time signal processing[M].2nd ed.USA:Prentice-Hall,1999:157-160.
[11]Miao J F,Chen W,Sun Y R,et al.Adaptively robust phase lockloop for low C/N carrier tracking in a GPS software receiver[J].Acta Automatic Sinica,2011,37(1):52-60.
[12]Yu W,Lachapelle G,Skone S.PLL performance for signals in the presence of thermal noise,phase noise,and ionospheric scintillation[C]//Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation,2006:1341-1357.
[13]Misra P,Enge P.Global positioning system,signals,measurements,and performance[M].2nd ed.USA:Ganga-Jamuna Press,2006.
[14]Shen B,Zhang Q L.A new method for analyzing the quantization effect of ADC in broadband QAM receiver[C]//Proceedings of IEEE International Conference on Communications,Circuits and Systems,2002,2:1262-1266.

