退化速率跟踪粒子滤波在剩余使用寿命预测中的应用*

范 彬，胡 雷，胡茑庆

(国防科技大学装备综合保障技术重点实验室，湖南长沙410073)

科学技术的加速发展使得现代复杂工程系统的结构越来越复杂，同时也使得保障其长期安全运行的难度越来越高，一旦发生事故都将造成巨大的损失和危害。为避免事故发生，就需要对设备剩余使用寿命进行预测，从而针对性地制定维护方案，提高系统的可靠性和安全性，降低维修成本。因此，在许多重要的领域，对设备的故障和剩余使用寿命进行预测已经受到越来越高的重视［1］。

近年来，国内外学者开发了很多可用于设备剩余使用寿命预测的方法［2－10］，如神经网络［5］、自回归滑动平均(Auto-Regressive and Moving Average，ARMA)时间序列模型［6］、隐半马尔可夫模型［7］、相关向量机［8］等基于数据驱动的方法，以及直接对具体零部件解析建模或仿真进行预测的基于物理模型方法［9，10］等。

其中，粒子滤波方法是一种基于数据与模型混合的预测方法，相比于传统的数据驱动预测方法，其预测结果中的不确定性信息对于决策者十分重要。粒子滤波基于大数定理，利用大量的“粒子”样本来近似状态变量的真实后验概率密度函数。尽管算法中的概率分布只是真实分布的一种近似，但因其非参数化的特点，得以摆脱解决非线性滤波问题时随机量必须满足高斯分布的制约，能表达比高斯模型更广泛的分布，也对变量参数的非线性特性有更强的建模能力。粒子滤波已在目标跟踪、航空航天、机器人定位、故障检测等领域得到成功应用，近年来也开始被学者应用于故障与寿命预测［11－13］。

尽管如此，粒子滤波目前仍不够成熟，除了算法本身的重要性函数选择、粒子退化和样本枯竭等问题［14］，在其应用于寿命预测时，还存在预测性能过度依赖于预测模型、对模型参数的初始分布过于敏感等问题［14，15］。因为对于不同的目标系统，选择的退化特征不同，需要针对性地选择合适的预测模型。而预测模型的复杂程度和准确程度大致成正比关系，使粒子滤波方法在剩余使用寿命预测上的应用及数据观测受到了明显的限制。除此之外，观测数据通常还受外界噪声等众多因素影响，增加了建模难度。

为解决缓变型的退化失效预测问题，提出一种基于退化速率跟踪粒子滤波(Degradation Rate Tracking-based Particle Filter，DRT-PF)的剩余使用寿命预测框架，该预测框架采用的预测模型只与预测特征的退化速率相关。由历史数据预测特征计算得到的退化速率信息，既可以用于模型的迭代更新，同时也可以辅助外推预测。由于预测模型不需要根据具体系统和特征进行调整，因此该框架对所有缓变型退化系统的预测都适用。

1 基本的粒子滤波预测方法

粒子滤波是一种基于序贯蒙特卡洛方法的非线性滤波方法，其基本思想是:首先依据系统状态变量的经验条件分布，在状态空间产生一组随机“粒子”，然后根据测量值不断调整粒子的权重和位置，通过调整后的粒子信息修正最初的经验条件分布。其实质是用粒子及其权重组成的离散随机测度近似相关的概率分布，并且根据算法递推更新离散随机测度。当样本容量很大时，这种蒙特卡洛描述就近似于状态变量真实的后验概率密度函数。

1.1 最优贝叶斯滤波

假设动态系统可以由数学模型描述，系统状态方程和测量方程分别为

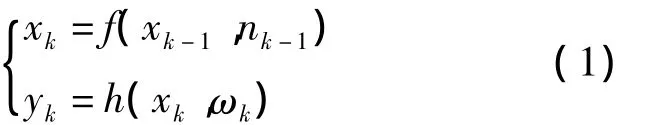
式中，xk为k时刻的状态值，yk为观测值，f(·)为系统状态xk－1的非线性函数，{nk－1，k∈N}是平稳噪声序列，h(·)为系统状态xk的非线性函数，{ωk，k∈N}是平稳噪声序列。

贝叶斯估计的递推过程分为预测和更新两步。

第一步，预测。假设在k－1时刻，状态的后验概率分布是已知的，则对于一阶马尔科夫过程，由根据系统的状态转移概率，推导出状态的先验概率

第二步，更新。即:

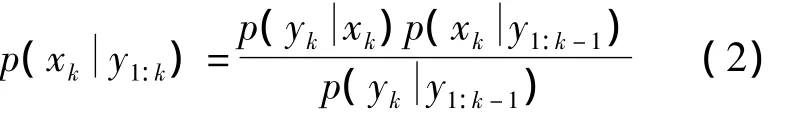
1.2 基本粒子滤波预测方法的实现

利用粒子滤波对某系统状态进行预测，所采用的策略是首先指定预测模型，然后根据已有的观测值对模型参数进行粒子滤波，通过迭代更新，使参数尽可能逼近实际值，最后将得到的模型参数估计值代入预测模型进行外推，实现对系统状态的预测。具体的实现步骤如下:

1)提取退化特征时间序列。根据历史观测数据，提取适用于预测的退化特征x。

2)获取先验模型知识。通过对历史数据退化特征的回归拟合或根据经验确定预测模型以及模型参数的初始分布。

3)粒子样本初始化。由先验概率p(x0)随机产生粒子群，令初始粒子权值

4)采样。相当于预测过程，即用状态方程f预测k+1时刻的状态

5)粒子状态更新。根据当前时刻的观测值，计算粒子样本与观测值的似然概率密度函数，以此更新粒子权值并对其进行归一化:

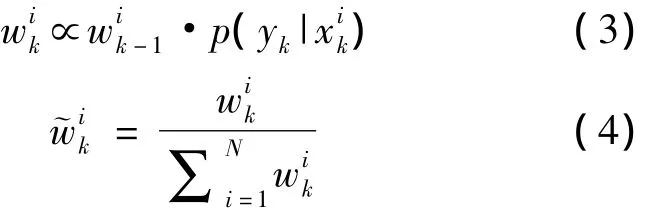
可得k时刻状态x的最小均方估计为

6)重采样。根据粒子权值大小进行重采样，得到新的粒子样本集

7)判断是否有新的观测值。在k+1时刻，如果有新的观测值，则转到第4步;否则，继续第8步。

8)将迭代更新完成的模型带入状态方程，对状态x进行外推预测。

9)预测结果统计。根据预测模型和更新得到的模型参数估计值，对所有粒子进行外推预测，至指定时刻或达到指定阈值。对N个粒子在指定时刻对应的预测值xi或达到指定阈值的时间进行统计，得到x在指定时刻的概率密度分布或x达到阈值时间的概率密度分布。

1.3 存在的问题

尽管基本的粒子滤波预测方法已经在某些领域得到了应用，但在其实现过程中，还存在一些不足之处:

1)退化特征的“质量”直接影响预测结果的准确程度。所谓的“质量”，指的是用于预测的退化特征反映目标系统退化趋势的能力。多数情况下，通过直接测量或初步提取得到的退化特征会受噪声等多种因素影响，只能反映系统的大致退化趋势。而将这样的退化特征用于粒子滤波预测，其观测噪声对模型的迭代更新会产生较大影响，使模型参数容易产生发散。

2)预测模型不易选择。在基本的粒子滤波预测方法中，预测模型的选择是必不可少的一个步骤，而且预测结果的准确程度很大程度取决于预测模型的准确与否。预测模型的细微改变，就可能导致预测结果的明显差异［15］，这严重影响了预测方法的整体稳定性。

3)预测模型参数较多，多维状态变量的粒子滤波难度加大。预测模型的选择，通常是根据对历史数据的拟合误差大小来判断的。简单的预测模型常常不能很准确地刻画历史数据的退化趋势，而准确的预测模型又比较复杂，模型参数多，会加大方法的实现难度，同时还会使算法的运算量成倍增长。

4)预测结果对模型参数的初始分布设置过于敏感。由于通常的预测模型参数在迭代更新阶段是没有实际观测值的，因此这些参数的初始分布设置直接决定了参数是否能够收敛及其收敛速度。尽管在文献［14］中，利用Dempster-Shafer理论成功给出了合适的模型参数初始分布，但实际上这种方法并不能保证始终得到合适的结果。

2 基于DRT－PF的预测框架

模型的选择及其参数的设置在传统的粒子滤波预测方法中占据了过于重要的地位，不仅占用了大量计算时间，而且在辨识过程中存在的较大不确定性也会影响预测结果的准确性。为了解决这个问题，从预测模型的角度，提出了一种DRT-PF预测方法。该方法为了提高预测方法的通用性，采用了一种根据退化速率来迭代更新退化状态的通用模型。对于不同的目标系统，其差异性体现为退化速率序列的不同，而预测模型是一致的。

2.1 通用预测模型

采用通用的预测模型式(6)代替之前需要进行实现辨识的预测模型，简化预测流程。

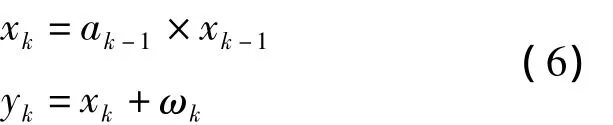
式中:yk为观测值，对应于原始的退化特征;xk为状态值，对应于预处理后的退化特征;ak为退化状态的退化速率，即后一时刻状态与前一时刻状态的比值xk+1/xk，也是状态方程中唯一的模型参数;ωk为观测误差。通用的预测模型将使粒子状态更加简单，只包括状态x和退化速率a，大大降低了计算量。另外，退化速率a在迭代更新阶段可以计算得到实测值，所以也能够对a进行重采样，因此能够明显降低模型参数的初始分布设置对于预测结果的影响。

2.2 原始特征的预处理

在实际预测中，通常只关心退化特征反映的系统退化趋势，而并不关心退化特征所包含的其他细节信息。而由于噪声等外界因素的影响，对于原始退化特征，退化速率的取值范围难以确定。所以要尽可能地去除噪声等外界因素的影响，这样得到的特征才能更直观地反映目标系统的退化趋势，同时有利于确定退化速率取值范围。另外，设备的退化过程是单调不可逆的。因此对初步提取的退化特征依次进行平滑和单调化的预处理，能够更适用于粒子滤波预测。图1为预处理前后的退化特征。

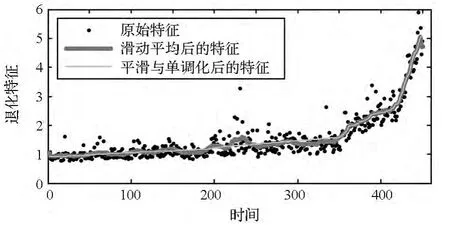
图1 预处理前后的退化特征对比示意图Fig.1 Comparison between raw degradation features and the pretreated features

2.3 历史数据的先验信息获取

在以上预测模型的基础上，从历史数据中可获取两方面的先验信息。一是预测模型中各参数的初始分布信息，与粒子样本的初始化相关;二是退化速率随状态x变化的分布情况，主要应用于外推预测阶段。先验信息的获取流程如图2所示。

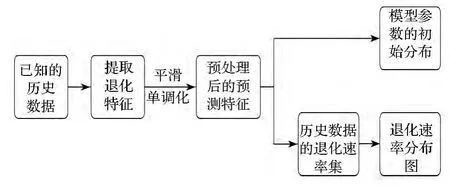
图2 先验信息获取流程图Fig.2 The flowchart for obtaining prior information

1)模型参数的初始分布。在进行预测之前，需要根据模型参数的初始分布进行粒子初始化，所以首先应确定预测模型参数的初始分布信息。粒子初始化使用一致分布，根据式(6)，需要进行初始化的参数包括:退化状态x，观测噪声标准差σ(ωk的标准差)，退化速率a。其中x与a在迭代过程中会进行重采样，所以其初始分布只需根据历史数据的初始观测值给出略大的区间即可。而σ则可以根据各组历史数据的原始信号与预处理后的信号残差进行统计得到。

2)不同阶段的退化速率分布图。a是预测模型中唯一的参数，体现系统的退化速度，更直接决定了对系统剩余寿命的预测结果，因此需要在预测过程中准确地估计退化速率的演变规律。一方面，因为设备退化是对时间单调变化的，所以退化特征经过平滑和单调化预处理后，退化速率a的取值上边界或下边界很容易确定(根据退化特征不同，可得a≤1或a≥1)，同时可以根据历史数据中a的极值情况确定其另一个取值边界。另一方面，由历史数据统计信息可以给出退化速率a随系统状态x变化的先验分布p(a|x)，作为预测阶段粒子状态的指导信息。首先将历史数据的退化速率对应到退化特征坐标轴上，再利用插值方法计算退化特征轴上的退化速率趋势曲线。最后对所有趋势曲线进行统计，在每个退化特征点上，对其相应的退化速率进行正态分布拟合，可以得到退化速率随特征变化的分布信息。

2.4 监测数据的预测

在获取了所需的先验信息之后，就可以对已有的监测数据进行预测。首先根据模型参数的初始分布信息，对N个粒子样本初始化，然后依次进行迭代估计和外推预测两个步骤，最后对所有粒子样本的状态进行统计，得到最终的预测结果。预测流程图如图3所示。

1)迭代估计阶段。首先对由已知的监测数据提取的退化特征进行平滑和单调化的预处理。然后利用基于通用预测模型的粒子滤波方法对模型参数进行迭代估计。在迭代估计过程中，将对退化状态值x和退化速率a分别进行重采样。

2)外推预测阶段。利用已知的观测数据完成对模型参数的迭代估计之后，再结合预测模型以及之前得到的退化速率分布图进行外推预测。设当前退化状态预测值为

那么，根据p(a|x)，随机生成当前状态下的先验退化速率aik(i=1，2，…，N)。然后再根据预测模型，可以得到下一步的退化状态值。

依次迭代预测，当退化状态预测值大于或小于失效阈值时，预测结束。对所有粒子的当前状态进行统计，就能得到失效时间预测的概率密度分布以及预测结果的置信区间等信息。

图3 监测数据预测流程图Fig.3 The flowchart of prediction scheme for monitoring data

3 实验验证与讨论

3.1 预测结果分析

图4所示为一个加速寿命实验的滚动轴承的剩余使用寿命预测结果。在图4(a)中，前500个数据点(数据点之间间隔10 s)被用来迭代更新预测模型，再用更新之后的模型结合退化速率分布图，对轴承500个数据点之后的状态进行预测。实际的失效时间位于预测结果的90%置信区间以内，表示预测结果有效。但因为用于迭代更新的数据点相对较少，所以预测结果的不确定度大。在图4(b)中可以看到，随着已知数据点的增加，预测结果逐渐逼近实际值，置信区间的宽度随已知数据点的增加而变窄，表示预测结果的准确性在升高，而不确定性在逐渐减低。

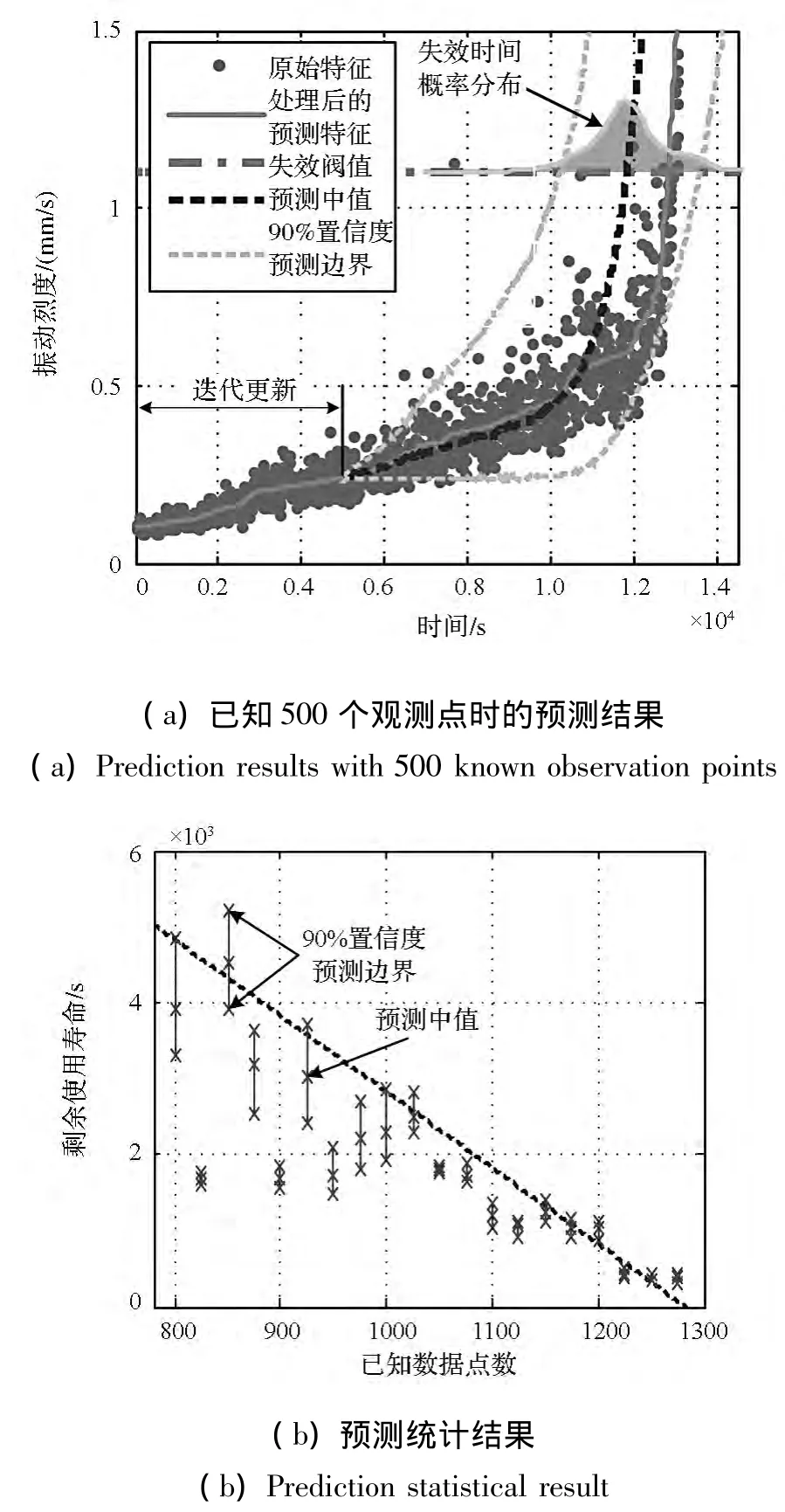
图4 轴承剩余使用寿命预测结果Fig.4 Prediction results of bearing remaining useful life

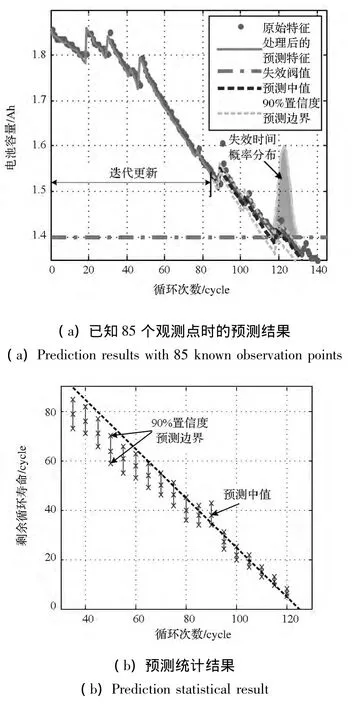
图5 电池剩余使用寿命预测结果Fig.5 Prediction results of battery remaining useful life

图5所示为NASA锂离子电池的循环寿命预测结果。锂离子电池循环寿命的退化特征为电池容量，呈逐步下降的趋势，与轴承的退化特征刚好相反，但对本文提出的预测方法没有影响。因为受到松弛效应的影响，锂离子电池的原始退化特征存在明显的非单调下降的部分，但采用文献［16］中的方法消除松弛效应之后，即可按照文中提出的预测框架进行处理。从图5(a)中可以看出，该方法能够对锂离子电池的循环寿命进行有效估计。而在图5(b)中，可以看到预测结果收敛速度更快，准确性更高。在图示范围内，预测中值与实际值的最大误差仅为11个循环。这是因为相对于图4，锂离子电池的预测特征与系统退化过程相关性更强，而且特征受其他因素影响更小，所以相应的预测效果也更好。

3.2 讨论

如前所述，通过对预测特征的退化速率进行跟踪，能够使粒子滤波对目标系统的状态估计迅速收敛，在预测阶段也能比较准确地逼近真实的退化趋势。预测结果的准确度随已知数据长度逐渐增减，不确定度随之下降。而且，对于无论是代表劣化程度(逐渐下降)还是代表健康程度(逐渐升高)的退化特征，该预测框架都同样适用，表现出了其良好的通用性，并在一定程度上简化了粒子滤波预测方法。

但是，对比两种不同系统的预测结果，可以发现预测特征仍然是对算法影响很大的一个因素，对于机械设备的预测尤为重要。由振动信号提取的预测特征往往受外界噪声等影响严重，如果预测特征和系统的退化趋势相关程度较低，那么算法的预测效果也会相对下降，所以如何提取与系统高度相关的预测特征还值得深入研究。

4 结论

本文提出了一种基于DRT-PF的预测框架。该方法对原始预测特征进行平滑和单调化处理，再利用历史数据中的退化速率信息辅助粒子滤波的迭代更新与外推预测。由于采用了通用的退化预测模型，因此该方法理论上对于任何缓变型退化系统的预测都适用。当拥有与系统退化趋势高度相关的预测特征和足够的历史数据时，该方法能够有效预测目标系统的剩余使用寿命。

References)

［1］Kruzic J J.Predicting fatigue failures［J］.Science，2009，325(5937):156－158.

［2］Bagul Y G，Zeid I，Kamarthi S V.Overview of remaining useful life methodologies［C］//Proceedings of the ASME 2008 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference，American Society of Mechanical Engineers，New York，2008:1391－1400.

［3］王小林，程志军，郭波.基于维纳过程金属化膜电容器的剩余寿命预测［J］.国防科学技术大学学报，2011，33(4):146－151.WANG Xiaolin，CHENG Zhijun，GUO Bo.Residual life forecasting of metallized film capacitor based on wiener process［J］.Journal of National University of Defense Technology，2011，33(4):146－151.(in Chinese)

［4］邓士杰，张英波，康海英，等.随机滤波模型在变速箱剩余寿命预测中的应用研究［J］.军械工程学院学报，2013(1):29－32.DENG Shijie，ZHANG Yingbo，KANG Haiying，et al.Research of stochastic filtering model for gear box residual useful life prediction［J］.Journal of Ordnance Engineering College，2013(1):29－32.(in Chinese)

［5］Shao Y，Nezu K.Prognosis of remaining bearing life using neural networks［J］.Proceedings of the Institution of Mechanical Engineers，Part I:Journal of Systems and Control Engineering，2000，214(3):217－230.

［6］Wang T Y，Yu J B，Lee J，et al.A similarity-based prognostics approach for remaining useful life estimation of engineered systems［C］//Proceedings of the International Conference on Prognostics and Health Management，IEEE，2008:1－6.

［7］Dong M，He D.A segmental hidden semi-Markov model-based diagnostics and prognostics framework and methodology［J］.Mechanical Systems and Signal Processing，2007，21(5):2248－2266.

［8］Di Maio F，Tsui K L，Zio E.Combining relevance vector machines and exponential regression for bearing residual life estimation［J］.Mechanical Systems and Signal Processing，2012，31:405－427.

［9］Li C J，Lee H.Gear fatigue crack prognosis using embedded model，gear dynamic model and fracture mechanics［J］.Mechanical Systems and Signal Processing，2005，19(4):836－849.

［10］Feng Z P，Zuo M J，Chu F L.Application of regularization dimension to gear damage assessment［J］.Mechanical Systems and Signal Processing，2010，24(4):1081－1098.

［11］Orchard M E.A particle filtering-based framework for on-line fault diagnosis and failure prognosis［D］.Atlanta:Georgia Institute of Technology，2007.

［12］Zio E，Peloni G.Particle filtering prognostic estimation of the remaining useful life of nonlinear components［J］.Reliability Engineering and System Safety，2011，96(3):403－409.

［13］Jin G，Matthews D E，Zhou Z B.A bayesian framework for on-line degradation assessment and residual life prediction of secondary batteries in spacecraft［J］.Reliability Engineering and System Safety，2013，113:7－20.

［14］He W，Williard N，Osterman M，et al.Prognostics of lithium-ion based on dempster-shafer theory and the bayesian monte carlo method［J］.Journal of Power Sources，2011，196(23):10134－10321.

［15］Wang D，Miao Q，Pecht M.Prognostics of lithium-ion batteries based on relevance vectors and a conditional threeparameter capacity degradation model［J］.Journal of Power Sources，2013，239(1):253－264.

［16］Tang S J，Yu C Q，Wang X，et al.Remaining useful life prediction of lithium-ion batteries based on the wiener process with measurement error［J］.Energies，2014，7(2):520－547.