部分频带干扰下伪码跟踪误差分析*
瞿 智,杨 俊,杨建伟
(国防科技大学机电工程与自动化学院,湖南长沙410073)
扩频测距系统中,精确的伪码同步是高精度测控和精密测量定轨的核心。部分频带干扰作为一种常见的干扰,可能会严重恶化伪码跟踪精度[1-2]。干扰环境中的伪码跟踪性能分析,是扩频测距系统设计的重要内容[2-4]。
传统方法分析部分频带干扰下的伪码跟踪性能时,假设干扰带宽比较宽,忽略了伪码的非理想随机特性:文献[5]结合跟踪环路的稳态特性分析了宽带白噪声条件下的伪码跟踪误差;文献[6-9]基于伪码功率谱给出了带限高斯白噪声条件下伪码跟踪误差的解析表达式。这些文献并未给出干扰带宽的定量要求,没有明确这些分析方法的适用条件。同时,一部分文献在分析单频干扰下的伪码跟踪性能时,考虑了伪码的非理想随机特性:文献[10]引入导航信号模型分析了单频干扰导致的伪码跟踪误差;文献[11-12]基于周期伪码的离散谱分析了单频干扰对延迟锁定环鉴相曲线的影响,并定义了干扰误差包络(Interference Error Envelope,IEE)和干扰平滑误差(Interference Running Average,IRA)两个参量来评估干扰对导航接收机测距性能的影响;文献[13-14]基于伪码的离散谱推导了单频干扰下伪码跟踪的最大误差和平均误差。
可以看出,在部分频带干扰下缺乏有效的分析来衡量不同干扰带宽情况下伪码跟踪性能的分析精度。忽略伪码非理想随机特性,基于伪码简化谱分析,计算成本小,但可能存在较大的分析误差。考虑非理想随机特性,基于伪码精细谱分析,分析精度高,但计算成本高。
1 系统与信号模型
1.1 伪码跟踪系统模型
扩频测距接收机的测距精度主要由码环的跟踪性能决定,伪码跟踪的基本结构如图1所示。接收机模拟通道假定为理想的带通滤波器,并考虑信号载频已剥离,那么接收机前端滤波器等效为带内幅度增益为1和截止频率为B/2的低通滤波器hr(t)。假定扩频信号的频率和相位能够精确跟踪,主要研究码环的跟踪性能。

图1 基带信号的伪码跟踪处理流程Fig.1 Code tracking process of baseband signal
不考虑热噪声,基带接收信号的模型为

式中,Cs表示接收的有用信号功率,s(t)表示经过理想低通滤波器的基带扩频信号,i(t)表示部分频带干扰,t0表示相对于起点的时间延迟,T表示积分时间。
1.2 部分频带干扰信号模型
假定干扰是高斯的,功率谱是带限且带内平坦的,即
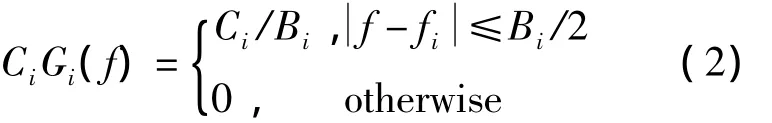
式中,Ci表示接收的干扰信号功率,Gi(f)表示干扰归一化功率谱,fi表示干扰中心频率,Bi表示干扰带宽。
1.3 扩频信号模型
目前,分析部分频带干扰下的伪码跟踪性能时,假定干扰带宽足够大,并忽略扩频码的非理想随机特性[7]。对于二进制相移键控(Binary Phase Shift Keying,BPSK)调制,扩频信号的归一化功率谱模型简化为

式中,Tc表示码片周期。这里假定伪码为理想随机码,仅关注了脉冲调制赋形,并没有体现扩频信号的伪随机特性。因此这个简化的平滑谱不能用来研究具体伪码跟踪性能的细节特征。
由于伪码并非理想的随机信号,并且短周期码广泛应用到全球导航卫星系统(Global Navigation Satellite System,GNSS)和遥测、跟踪和指挥(Telemetry,Track and Command,TT&C)中的精密测距和定位,基于简化的平滑谱模型的分析不能满足高精度测距应用的需求。充分考虑短周期伪码的非理想随机特性和短周期特性,引入扩频信号模型
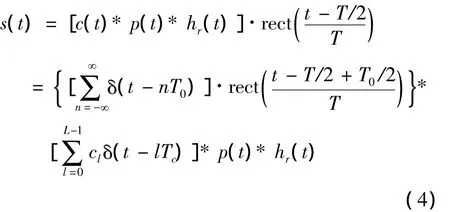
式中,*表示卷积,c(t)表示伪码序列,p(t)表示脉冲编码赋形,L表示伪码序列长度,T0表示伪码周期,且T=KT0,K∈Z+。
利用傅里叶变换,由式(4)可以得到扩频信号频谱为
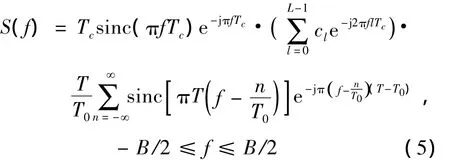
由于扩频解扩的积分时间一般较长,扩频信号精确的功率谱为
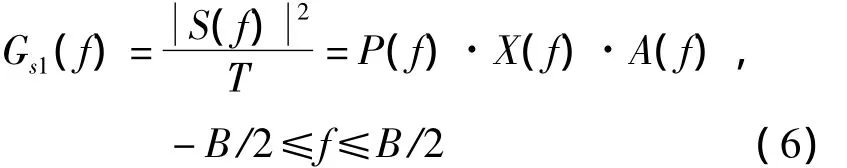
其中:
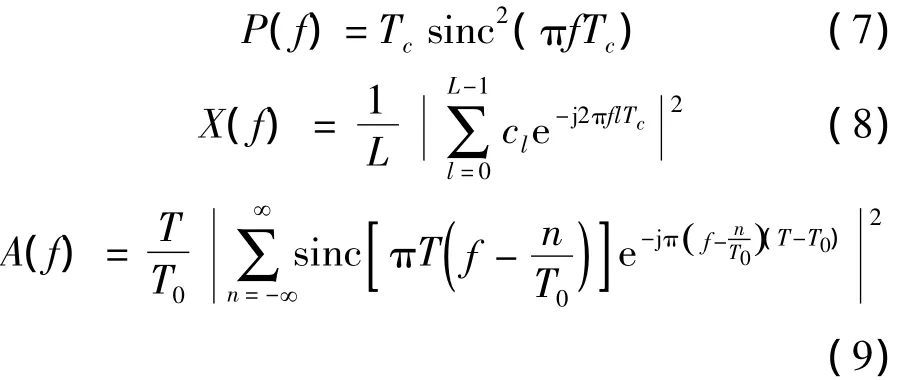
可以看出周期伪码信号的功率谱由三部分组成,第一部分P(f)说明功率谱的基本形状由脉冲编码赋形决定,第二部分X(f)体现了伪码的非理想随机特性对功率谱的影响,第三部分A(f)反映了积分时间对功率谱细节特征的影响。
对于理想随机码,X(f)=1,并且取T=T0时,式(6)等价于式(3)。对于短周期码,X(f)存在很大的幅度波动,这里以GPS L1 C/A码为例,由式(8)得到PRN1~PRN32的功率谱最大波动量,见图2。
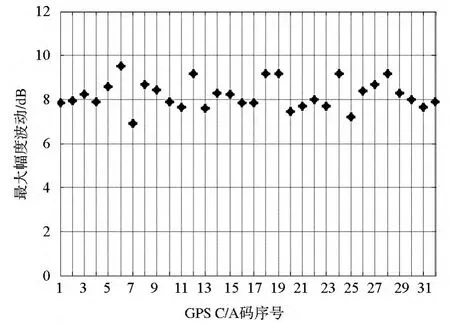
图2 GPS L1 C/A码功率谱最大波动量Fig.2 Maximum fluctuation of power spectrum of GPS L1 C/A codes
可以看出,伪码非理想随机特性导致的功率谱波动量达到6.91~9.53dB,这可能导致较大的伪码跟踪误差变化。尤其在部分频带干扰带宽较窄的情况下,扩频信号功率谱局部频段的幅度波动可能严重恶化伪码跟踪性能。下面基于精细功率谱,定量分析伪码非理想随机特性导致的伪码跟踪精度变化。
2 伪码跟踪误差特性分析
2.1 伪码跟踪误差
当接收机码环采用相干鉴相时,部分频带干扰下伪码跟踪误差的方差为[8]

式中,BL表示码环等效噪声带宽,τ表示码环超前滞后间隔。
将式(2)代入式(10),可得
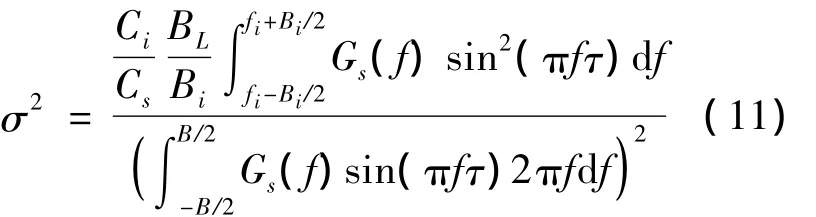
式(11)表明伪码谱特性很大程度上影响着部分频带干扰下的伪码跟踪误差,并且随着干扰中心频率和干扰带宽的变化,跟踪误差的变化也与伪码功率谱密切相关。伪码非理想随机特性导致的功率谱波动,将引起伪码跟踪误差的变化。尤其在干扰带宽较窄时,从式(11)的分子部分可以看出,跟踪性能对伪码功率谱局部频段的特征将更加敏感。
2.2 相对误差系数
为定量分析伪码非理想随机特性对跟踪精度的影响,这里引入相对误差系数
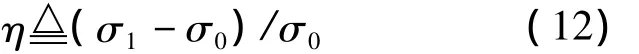
式中,σ0表示基于简化的扩频信号功率谱Gs0(f)得到的跟踪误差,σ1表示基于精细的扩频信号功率谱Gs1(f)得到的跟踪误差。
相对误差系数反映了伪码非理想随机特性导致的功率谱波动对跟踪误差的影响,也可以看作部分频带干扰下准确的跟踪误差相对于基于简化谱分析得到的跟踪误差的相对误差,以此来衡量简化谱分析的适用性。
由于在宽带范围内积分,伪码功率谱波动对积分结果的影响可忽略[2],那么由式(11)和式(12)可以得到

从式(13)可以看出,相对误差系数不再与干信比和环路等效噪声带宽等参量有关。同时,码环超前滞后间隔τ较小(一般情况下仅0.001~1个Tc),其对相对误差系数的影响非常小。总体来看,相对误差系数主要受伪码谱特性和干扰特征参量的影响。
这里首先针对两种典型情况予以说明。
当干扰带宽极窄时,即Bi〈1/(5T)时,式(13)可以化简为
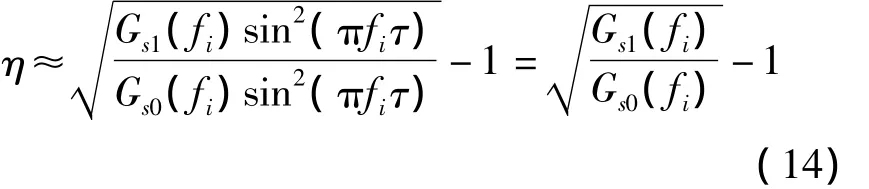
根据式(3)、式(6)和式(14),可以得到

式中,μ表示伪码功率谱最大波动量。
由式(15)可以看出,在干扰带宽较窄时,伪码功率谱波动越大或积分时间越长,基于两种谱的误差分析差异越大,反映出基于简化谱的分析也越不准确。以GPS L1 C/A PRN 5码为例,即使在T=T0时,相对误差系数也高达1.68。也就是说,此时的伪码跟踪误差是基于简化谱分析结果的2.68倍,这说明基于简化的平滑谱分析已完全不可用。
另一种情况,是Bi〉5/T0,这在工程实践中比较常见。随着干扰带宽的增加,相对误差系数将越来越小直至接近于0,这说明基于简化的平滑谱的跟踪误差分析将逐渐适用。这里需要给出明确的界限以便于实际应用中能够确定适用简化谱的条件。由于伪随机码的多样性,下面将以GPS L1 C/A码为例进行数值分析,给出各自的简化谱适用条件,并通过统计分析给出简化谱适用的经验条件。
3 数值分析
干扰带宽是影响基于两种谱分析的性能差异的主要特征参量,这里基于不同的干扰带宽对比两种跟踪精度分析。数值分析参数见表1。

表1 数值分析参数表Tab.1 Parameters of numerical analysis
当干扰带宽为100Hz时,基于两个谱分析的伪码跟踪误差和相对误差系数分别见图3和图4。可以看出,当干扰带宽较小时,两者的差异明显,相对误差系数可达1.681。这说明伪码的非理想随机特性在较窄的部分频带干扰中对跟踪精度的影响较大,不能忽略,此时基于简化谱的伪码跟踪精度分析已不可用。
当干扰带宽为300kHz时,基于两个谱分析的伪码跟踪误差和相对误差系数分别见图5和图6。两个跟踪误差趋于一致,相对误差系数小于0.06。这说明在干扰带宽较宽时,伪码的非理想随机特性对码跟踪误差的影响很小,跟踪精度的分析可完全采用简化的平滑谱以减少计算量。
由前面的分析可知,分别基于简化的功率谱和精细的功率谱得到伪码跟踪误差的差异随着干扰带宽的增加而减小。只有这个差异小于一定的条件时,基于简化谱的分析才是适用的。为此,设定当相对误差系数小于0.2时,即伪码非理想随机特性引起的跟踪误差波动小于20%时,可以认为基于简化谱的分析是适用的。
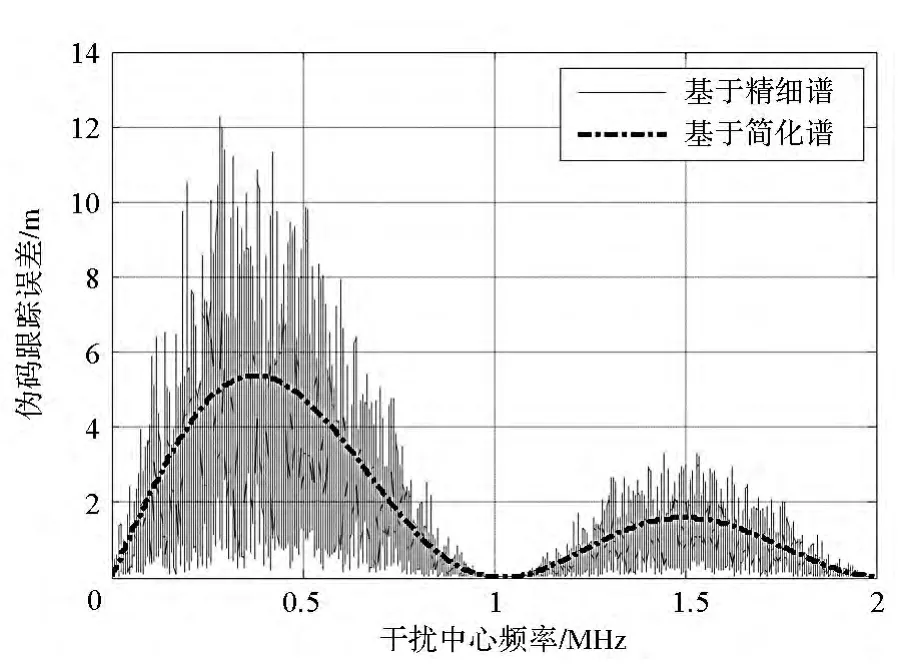
图3 基于两种谱的跟踪误差对比(Bi=100Hz)Fig.3 Comparison of tracking error based on two spectrums(Bi=100Hz)
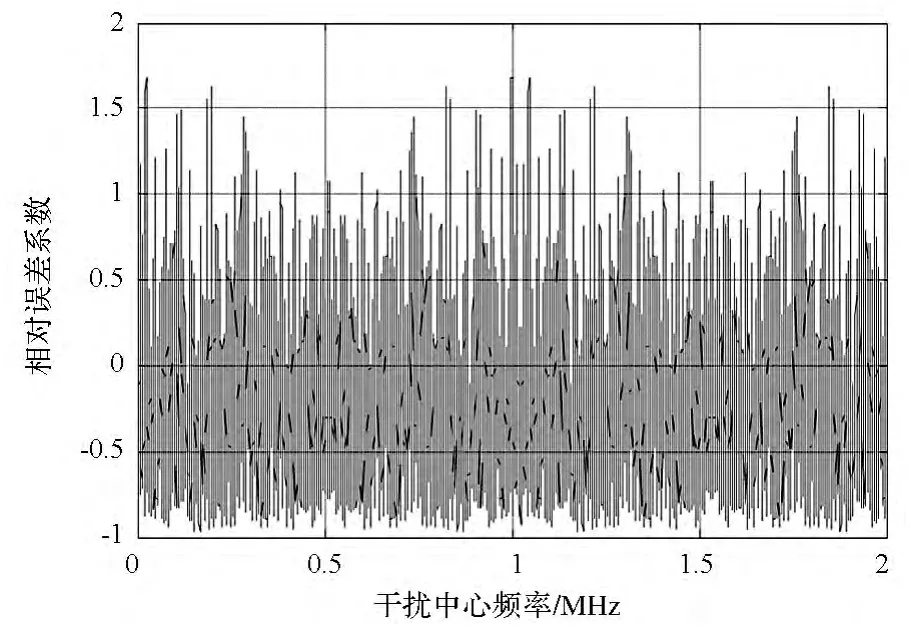
图4 相对误差系数(Bi=100Hz)Fig.4 Relative error coefficient(Bi=100Hz)

图5 基于两种谱的跟踪误差对比(Bi=300kHz)Fig.5 Comparison of tracking error based on two spectrums(Bi=300kHz)
不同干扰带宽条件下,GPS L1 C/A PRN 5最大的相对误差系数见图7。随着干扰带宽的增加,最大相对误差系数逐渐减小,基于简化谱的分析也更加准确。可以看出,当干扰带宽大于约200kHz时,基于简化谱的分析误差小于20%。
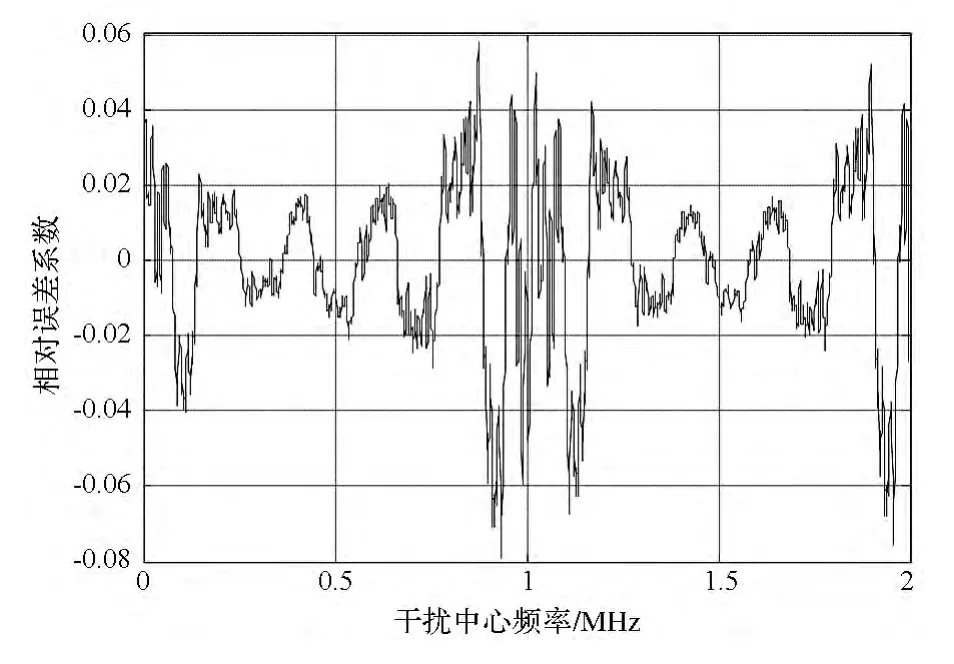
图6 相对误差系数(Bi=300kHz)Fig.6 Relative error coefficient(Bi=300kHz)

图7 最大相对误差随干扰带宽的变化特性(GPS C/A PRN 5)Fig.7 Maximum relative error versus interference bandwidth(GPS C/A PRN 5)
基于简化谱的分析误差主要是由伪码的非理想随机特性引起的,但不同伪码的非理想随机特性存在一定的差异。这里给出GPS L1的32个C/A码在基于简化谱的分析误差不超过20%时的最小干扰带宽,见表2。
从表中可以看出,PRN 17的非理想随机特性对误差分析的影响最大,干扰带宽大于285kHz时,才能基于简化谱进行误差分析,而PRN 32的非理想随机特性对误差分析的影响相对较小,只要干扰带宽大于26kHz,基于简化谱的分析误差就小于20%。总体来看,对于大多数码,干扰带宽大于100kHz(即伪码周期的频率的100倍)时,相对误差系数小于20%。基于保守分析,对于所有伪码,干扰带宽大于300kHz(300/T0)时,基于简化谱的分析误差可忽略,这可以作为适用基于简化谱分析的一般条件。同时,可以将此带宽作为划分窄带干扰和宽带干扰的分界线。当基于简化谱的分析误差小于20%时,伪码非理想随机特性可忽略,认为干扰为宽带干扰;当基于简化的分析误差大于20%时,伪码非理想随机特性对码跟踪精度的影响不可忽略,此时干扰为窄带干扰。

表2 最小干扰带宽(GPS C/A码)Tab.2 Minimum interference bandwidth(GPS C/A codes)
4 结论
本文定量分析了伪码非理想随机特性对部分频带干扰下的伪码跟踪精度的影响。引入能够描述伪码非理想随机特性的精确功率谱模型,分析了伪码跟踪误差,并以传统的基于简化的平滑谱模型得到的伪码跟踪误差为基准进行了对比分析。当干扰带宽较宽时,伪码非理想随机特性对跟踪误差的影响较小,但当干扰带宽较小时,基于平滑谱模型得到的伪码跟踪性能的分析误差较大。本文定义了相对误差系数,能够定量描述由伪码非理想随机特性导致理论分析的相对误差。给出了GPS L1 C/A码在相对误差小于20%时的最小干扰带宽,并将这个带宽作为简化谱适用的条件门限。分析发现,最小干扰带宽不超过伪码周期的频率的300倍。当干扰带宽大于这个带宽时,伪码非理想随机特性在伪码跟踪精度分析中可忽略,反之,则需要考虑非理想随机特性导致的扩频信号功率谱波动,只有基于精细的伪码谱模型才能得到精确的伪码跟踪误差分析。
References)
[1]Daher J K,Harris J M,Wheeler M L.An evaluation of the radio frequency susceptibility of commercial GPS receivers[J].IEEE Aerospace and Electronic Systems Magazine,1994,9(10):21-25.
[2]Kaplan E D,Hegarty C.Understanding GPS:principles and applications[M].2nd ed.USA:Artech House,2006.
[3]Misra P,Enge P.Global positioning systems:signal measurements and performance[M].2nd ed.USA:Ganga-Jamuna Press,2010.
[4]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2012.XIE Gang.Principles of GPS and receiver design[M].Beijing:Publishing House of Electronics Industry,2012.(in Chinese)
[5]Van Dierendonck A J,Fenton P,Ford T.Theory and performance of narrow correlator spacing in a GPS receiver[J].Navigation,1992,39(3):265-283.
[6]Betz J W.Effect of narrowband interference on GPS code tracking accuracy[C]//Proceedings of the National Technical Meeting of the Institute of Navigation,2000:16-27.
[7]Betz J W.Effect of partial-band interference on receiver estimation of C/N0:theory[C]//Proceedings of the National Technical Meeting of the Institute of Navigation,2001:817-828.
[8]Betz J W,Kolodziejski K R.Generalized theory of code tracking with an early-late discriminator part I:lower bound and coherent processing[J].IEEE Transactions on Aerospace and Electronic Systems,2009,45(4):1538-1550.
[9]Betz J W,Kolodziejski K R.Generalized theory of code tracking with an early-late discriminator part II:noncoherent processing and numerical results[J].IEEE Transactions on Aerospace and Electronic Systems,2009,45(4):1551-1564.
[10]Jang J,Paonni M,Eissfeller B.CW Interference effects on tracking performance of GNSS receivers[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(1):243-258.
[11]Motella B,Savasta S,Margaria D,et al.An interference impact assessment model for GNSS signals[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation,2008:900-908.
[12]Motella B,Savasta S,Margaria D,et al.Method for assessing the interference impact on GNSS receivers[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(2):1416-1432.
[13]Liu Y Q,Ran Y H,Ke T,et al.Code tracking performance analysis of GNSS signal in the presence of CW interference[J].Signal Processing,2011,91(4):970-987.
[14]Liu Y Q,Ran Y H,Ke T,et al.Characterization of code tracking error of coherent DLL under CW interference[J].Wireless Personal Communications,2012,66(2):397-417.

