作战协同关系超图模型*

贾 珺，吴元立，贺筱媛，胡晓峰

(1.国防大学信息作战与指挥教研部，北京100091;2.国防大学研究生院，北京100091)

作战协同关系指的是无隶属关系的两个以上部队在共同遂行作战任务时所构成的相互协助、配合的关系［1］。在仿真建模领域对作战协同关系的研究，一般是通过建模的方法，并将其放在作战体系或者指挥体系模型之中，通过自底向上或者自顶向下两种方式来完成的。

自底向上指的是首先通过Agent等方式建立作战实体模型，在统一的环境中研究实体之间协同关系的变化或形成的机理等。例如赵亚伟通过定义和结构化描述Agent之间的协同关系，实现了对协同关系变化的研究［2］;冯磊等通过建立CGF Agent认知体系结构，设计了协同行为建模框架［3］等。而自顶向下指的是首先建立作战体系的模型，在此基础上分析其中各要素之间的协同关系和演化规律等内容。例如王庆贵、朱涛等通过复杂网络对作战体系进行建模，并分析了网络的基本特征［4－5］;朱江等通过构建三层结构，采用超网络模型对作战体系进行建模描述［6］;张巍等采用群体组织协同关系模型，对基于任务描述的协同关系进行了建模［7］等。以上两种方式中协同关系的形式化建模，都是将其简化为一般网络中两两节点之间的连接。在此基础上，虽然还有将两种方式结合进行作战体系建模的［8］，但在协同关系描述方面同样采用上述方法。

上述文献中的协同关系建模方法，首先是将协同关系以二分图的形式进行描述。例如对于作战体系中的A，B，C三个作战实体而言，在某一段作战过程1中，部队A，B发生过协同，B，C发生过协同，A，C发生过协同;而在另一次作战过程2中，部队A，B，C共同协同过，那么这两次作战行动的已有协同关系采用二分图的方式可以表示为图1中上半部分。二分图虽然能够比较明确地反映实体间作战协同的关系，但是由于图中的节点异质，无法通过度或者聚类系数等进行进一步的分析。为了解决这一问题，将二分图通过投影变换成为简单图，去掉图中的任务节点，只留下作战实体，使协同关系图中的节点同质，如图1中下半部分所示。

图1 作战协同关系二分图与简单图Fig.1 Bipartite graph and simple graph of operation cooperative relation

在图1中可以看到，由于描述方法的缺陷，这种通过简单投影变换构造的协同关系描述方法对于多个部队之间的协同产生了歧义。而且这种协同关系描述模型带来的歧义使得协同关系的进一步分析更加难以实现。在社会科学领域研究中，已经有人就科研合作网络的建模和分析使用了超图相关方法［9］，但在作战研究领域还没有人使用。因此，贾珺等采用基于超图的方法对作战过程中的各类协同关系进行建模，避开了上述问题。在此基础上进行了实验分析，证明了建模方法的可行性。

1 相关概念

1.1 超图基本概念

超图概念是Berge于1970年提出的，他在《Graphs and Hypergraphs》一文中第一次系统地建立了无向超图理论，并应用拟阵来研究超图理论在运筹学方面的应用［10］。超图的定义是:

设V={v1，v2，…，vn}是一个有限集，若:

称二元关系H=(E，V)为一个超图。其中V的元素v1，v2，…，vn称为超图的顶点，E={e1，e2，…，em}是超图的边集合，集合ei={vi1，vi2，…，vij}(i=1，2，…，m)称为超图的边［11］。

1.2 作战协同基本概念

作战协同表现为战场上的多个力量为了达成同一作战目的，相互之间协调一致的行动。按照规模，可以将作战协同分为战略协同、战役协同和战术协同;按照军兵种，可以分为陆空协同、海空协同、陆海协同等;按照行动，可以分为火力战协同、电磁战协同和心理战协同等;按照保障，可以分为作战保障协同、后勤保障协同和装备保障协同等［12］;按照协同形成的原因，可以将作战协同分为他组织和自组织两类。但是无论协同的规模和成因如何，对于作战过程中已发生的协同都包含时间和空间两种关系。

协同的空间关系具体指的是相互协同的作战力量在行动中空间的相对位置，例如在某次阵地进攻中，从左翼进攻的一营和从右翼进攻的二营之间的空间相对位置。协同的时间关系则具体指的是相互协同的作战力量在行动中时间的顺序，例如在防空作战中雷达的预警跟踪和防空火力的开火两者间的先后顺序。这两种关系的综合，构成了作战协同关系，在实际的作战协同中，这两种关系总是共同存在的。将时空两种关系进行综合考虑，对于作战过程中已发生的各类协同关系，从形象化描述角度出发，将不同类型的作战协同抽象为同一类型统一进行建模。

2 作战协同关系模型

作战协同关系是与作战过程或者时间息息相关的，对于某个时间点而言，协同关系是固定的;但若从一段时间来考量，可以发现其在整个作战过程中是不断变化的。因此对于作战协同关系的建模，首先要通过节点、任务等对协同关系建立其静态的模型，在此基础上引入时间系数后，才能通过相关特征参数对其动态特征的变化进行分析。

2.1 模型定义

根据前面的描述，协同关系指的是无隶属关系的两个以上部队间基于某个任务而产生的相互配合、协作的关系。那么可以首先通过下面的形式化方式对其进行描述。

定义1(作战协同关系)对于某个作战任务Tj，若有n个部队{vj1，vj2，…，vjn}共同参与完成，那么定义这n个部队之间产生作战协同关系ej，且ej={vj1，vj2，…，vjn}。

对于整个作战过程而言，对某个时间节点前各力量之间已发生的协同关系，可以首先采用矩阵的方式进行描述。

定义2(作战协同关系矩阵)若在整个作战过程中的某个时间点t0前，共产生了m个协同关系，并且已知作战力量和协同关系之间可以用ej={vj1，vj2，…，vji}(j=1，2，…，m)表示，那么定义协同矩阵B t0为:

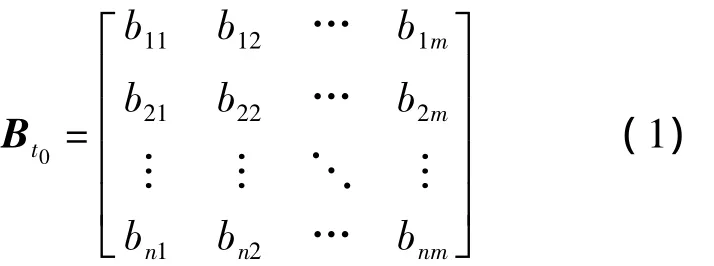
其中，行集合表示每个作战力量vi对应的协同关系，列集合表示每个协同ej与作战力量的对应关系。若vi∈ej，那么bij=1，否则bij=0。

由式(1)可知，若对于持续时间为T的整个作战过程而言，其总体的协同关系矩阵可以表示为:

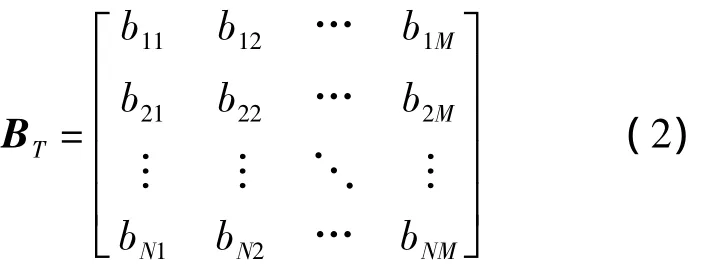
其中，行集合{v1，v2，…，vN}为所有与协同相关的作战力量，列集合{e1，e2，…，eM}为全部协同关系。

在作战协同关系及矩阵的基础上，可以定义基于超图的作战协同关系模型。

定义3(作战协同超图模型)若作战力量可用有限集V={v1，v2，…，vn}表示，如果存在:

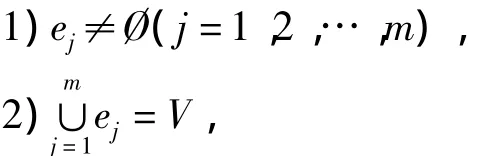
称二元关系H=(E，V)为作战协同超图模型。其中V={v1，v2，…，vn}称为超图的顶点集合，作战协同关系ej={vj1，vj2，…，vji}(j=1，2，…，m)称为超图的边，E={e1，e2，…，em}称为作战协同关系超图的边集合。根据超图定义，图1中的两类作战协同关系采用超图可以表示为图2形式。

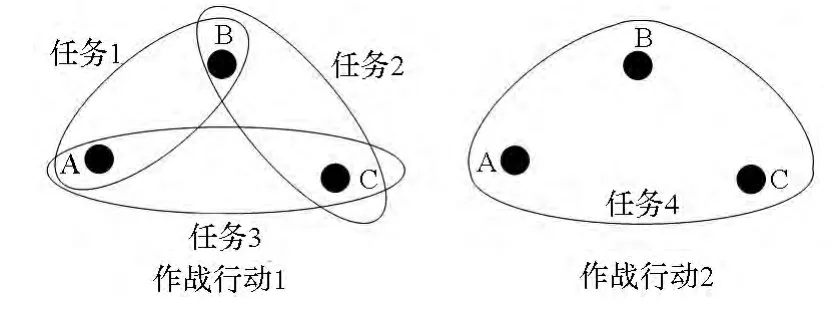
图2 作战协同关系超图Fig.2 Hypergraphs of operation cooperative relation

由图2可以看出，超图方式解决了由二分图向简单图投影时所带来的歧义问题。同时，超图模型可以解决二分图中节点异质难以分析的问题。

定理1若对于某时刻t0分别构建关系矩阵B和作战协同超图H，则有B为H的关联矩阵(根据作战协同超图模型H和作战协同关系矩阵B的定义可以得到两者之间关系)。

推论1.1对于n×m的关系矩阵B，有R(B)=min(n，m)。(证明略)

2.2 相关特征参数

在进行了上述模型定义之后，就可以使用关系矩阵和超图模型对作战中的协同关系进行描述了。在此基础上，为了满足下一步的分析需求，还要参照复杂网络和超图的相关概念，对作战协同超图模型中的一些特征参数进行定义。

定义4(作战协同超图模型H中顶点的度)对于任意顶点vi，定义顶点的度，其中bij为作战协同超图模型H的关联矩阵B中的元素。

作战协同超图中顶点度的物理意义反映的是与顶点vi相连接的边的数量，其军事意义是指在作战过程中指定作战力量与其他作战力量发生过的协同的次数之和，它能够从一定层面反映指定作战力量的重要性。通过对顶点度的统计，可以找出在作战过程中起重要作用的作战力量。同时，为了考量作战力量之间的关系，还要进行如下定义。

定义5(作战协同超图模型H中顶点的关联系数)对于任意顶点va和vb，两顶点之间的关联系数，其中baj和bbj分别为顶点va和vb在作战协同超图模型H的关联矩阵B中对应行的元素。

顶点关联系数的物理意义是两两顶点之间存在共同边的数量。其军事意义是指在整个作战过程中两个指定的作战力量进行协同的次数之和。由于作战过程中协同一般由自组织和他组织两种方式形成，那么协同的产生也就存在偶然性和必然性两种原因。通过对关联系数的统计所得出的协同次数，可以从一定层面反映出作战过程中两两作战力量相互协同的必然性，而这种必然性可以为进行作战力量编配提供参考。这种方式突破了传统对于协同的因果分析，通过数据找出力量之间可能存在的关联关系，以这种关系直接指导协同计划拟制或进行力量编组等相关工作。

根据上述定义，还可以得到以下相关定理和推论。

定理2根据关联系数构建的矩阵C为超图H的连接矩阵，其中C的每行和每列都与H的顶点相关，且超图H的关联矩阵和连接矩阵存在关系为C=BBT－D。其中D为对角线上元素为顶点度数的对角矩阵。

证明:易得到

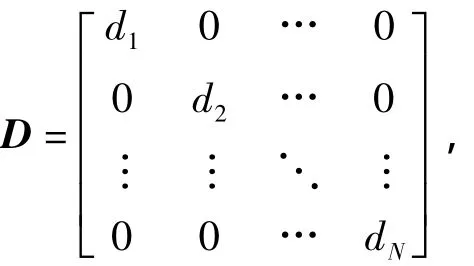
证毕。

推论2.1对于N×N的连接矩阵C，有m－1≤R(C)≤m。(证明略)

通过上述定义及相关定理推论，可以对作战协同关系进行形式化的描述，并可以进行一定程度的定量化分析，下面用一个实际的作战实验为基础，对其中的火力协同关系进行建模，以验证模型的可用性。

3 实验分析

现有某大型仿真系统可以实现对战役级别的作战过程进行仿真模拟。其基本作战力量模型可划分为地面营、海上舰艇和空中飞机三个主要类别。现通过前面定义的模型和相关特征参数，对某以联合作战为主要行动样式的想定中产生的相关数据进行分析，以想定中的火力协同为例验证模型的可用性。该想定涉及各类基本作战力量共计125个，其中各类地面营21个，各类海上舰艇22艘，各类飞机82架。

3.1 数据提取

想定在系统中运行后产生的各类数据以结构化的形式存储在特定的数据库中，具体包括作战实体、交互事件等几个专用表。作者根据具体的数据格式，使用C#语言构建了专用的数据提取工具，对某一时间段内想定中各作战力量之间的火力协同关系进行了提取。相关数据包括火力协同任务32个，共涉及各类基本作战力量共计108个，具体数据见表1(由于篇幅原因这里只写出部分数据)。

表1 某想定中协同关系相关数据Tab.1 Data of the operation cooperative relation in scenario

表1中的数据反映的是整个作战过程中协同任务及对应的作战力量集合。根据定义1，表中的每一行可表示为一个标准的协同关系。其中每行为协同关系ej，相关作战力量为{vj1，vj2，…，vjn}。

3.2 模型构建

在上述数据基础上，为了更清楚地显示协同关系，对数据进行截取。根据定义2，设定时间节点t0，截取完成时间T≤t0的任务，可以得到作战协同关系矩阵B t0(缩略)为:

由矩阵B t0可知，当设定条件T≤t0时，抽取到的是前6个协同关系，其相关作战力量共计26个。在该关系矩阵的基础上，可以得到作战协同网络的二分图，如图3所示。

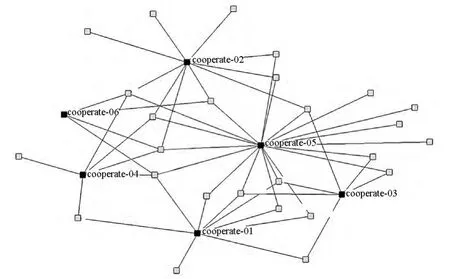
图3 某想定中t0时间内火力协同关系二分图Fig.3 Bipartite graph of operation cooperative relation in a scenario before t0

图3中深色点为火力协同任务，浅色点为相关作战力量。再根据定义3可以得到相对应的作战协同超图模型，如图4所示。

由图4可以看到，图中点为作战力量，圈为火力协同关系。这种超图避免了前面提到的二分图节点异质和简单映射图的歧义等问题，可以正确地反映各作战力量之间的火力协同关系。其他协同关系以此类推，都可以采用超图模型进行形象化表示。

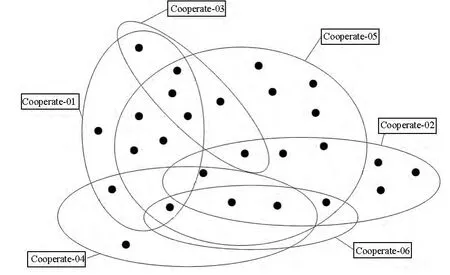
图4 某想定中t0时间内火力协同关系超图Fig.4 Hypergraph of operation cooperative relation in a scenario before t0

3.3 基于特征参数的分析

在构建完成上述模型的基础上，可以对作战力量的协同次数进行分析，即根据定义4计算顶点度之后再进行统计，研究协同网络顶点度的分布规律，如图5所示。

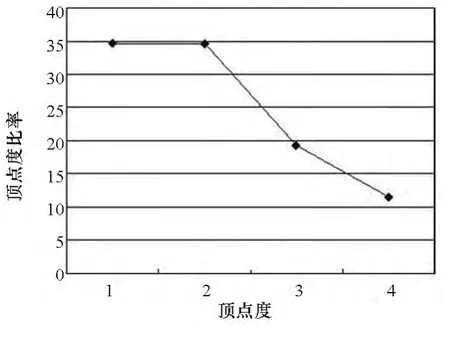
图5 作战协同超图顶点度分布图Fig.5 Distribution diagram of vertex's degree

图5是t0时刻前作战力量协同关系的度分布。从图5中可以看出作战力量的火力协同关系分布初步具备幂律的特性，但并不明显。对于这种协同关系分布的规律研究，还要建立在多次大规模实验的基础上，对其数据进行统计以期发现其中规律。同时，还可以对作战力量之间的协同频度进行分析，即根据定义5计算顶点的关联系数，研究作战过程中作战力量之间的协同规律，如图6所示。

图6 关联系数统计分布图Fig.6 Distribution diagram of correlation coefficient

由图6可以看到，在作战协同中关联系数主要用来表征作战力量的协同次数，对于关联系数较高的作战力量组合，说明在作战过程中这些作战力量的协同存在一定的经常性。因此在拟制协同计划或者进行作战力量编组时，可以考虑将关联系数较高的作战力量放置在一起。

4 结论

本文使用了超图模型对作战协同关系进行了建模，并定义了能够表现协同关系特征的顶点度和关联系数等参数，在此基础上进行了实验，验证了模型的可用性。对于作战协同的研究，这仅仅是一个基础。下一步还需要在超图模型基础上，构建更能够反映协同特征的参数，并基于成熟的仿真系统，通过多次模拟实验产生大量数据，采用挖掘分析的方式(例如基于关联系数频繁项的数据挖掘等)，对协同形成的机理、协同中可能存在的规律以及协同的利用等内容进行更深一步的研究。

References)

［1］中国人民解放军军语［M］.北京:军事科学出版社，2011.The people's liberation army's military terminology［M］.Beijing:Military Science Press，2011.(in Chinese)

［2］赵亚伟，张海盛.基于Agent的协同模型关系研究［J］.系统仿真学报，2003，15(11):1529－1532.ZHAO Yawei，ZHANG Haisheng.Research on cooperative relation model based on agent［J］.Journal of System Simulation，2003，15(11):1529－1532.(in Chinese)

［3］冯磊，查亚兵，胡记文，等.CGF中的协同行为建模技术［J］.系统仿真学报，2013，25(4):591－597.FENG Lei，ZHA Yabing，HU Jiwen，et al.Cooperative behavior modeling technology in CGF［J］.Journal of System Simulation，2013，25(4):591－597.(in Chinese)

［4］王庆功，沈寿林，袁昌平.基于复杂网络的作战体系网络模型分析［J］.指挥控制与仿真，2013(1):6－10.WANG Qinggong，SHEN Shoulin，YUAN Changping.Combat system network model analysis based on complex network［J］.Command Control＆Simulation，2013(1):6－10.(in Chinese)

［5］朱涛，常国岑，张水平，等.基于复杂网络的指挥控制信息协同模型研究［J］.系统仿真学报，2008，20(22):6058－6060.ZHU Tao，CHANG Guocen，ZHANG Shuiping，et al.Research on model of command and control information cooperation based on complex networks［J］.Journal of System Simulation，2008，20(22):6058－6060.(in Chinese)

［6］朱江，刘大伟，陈俊.作战体系超网络模型及应用［J］.指挥控制与仿真，2013，35(2):13－16.ZHU Jiang，LIU Dawei，CHEN Jun.Hyper-network model of combat system and use case［J］.Command Control＆Simulation，2013，35(2):13－16.(in Chinese)

［7］张巍，曾亮，李思昆.基于描述任务逻辑的群体组织协同关系模型［J］.计算机工程与科学，2013，35(1):94－99.ZHANG Wei，ZENG Liang，LI Sikun.Coordinative relationship model for groups organization based on the description logic of tasks［J］.Computer Engineering＆Science，2013，35(1):94－99.(in Chinese)

［8］朱江，刘大伟，李翼鹏.作战超网络多Agent模型［J］.计算机科学，2012，39(7):44－47.ZHU Jiang，LIU Dawei，LI Yiping.Combat super network multi-agent model［J］.Computer Science，2012，39(7):44－47.(in Chinese)

［9］胡枫，赵海星，何佳倍，等.基于超图结构的科研合作网络演化模型［J］.物理学报，2013(19):539－546.HU Feng，ZHAO Haixing，HE Jiabei，et al.An evolving model for hypergraph-structure-based scientific collaboration networks［J］.Acta Physica Sinica，2013(19):539－546.(in Chinese)

［10］Berge C.Graphs and hypergraphs［M］.New York:Elsevier，1973.

［11］王志平，王众托.超网络理论及其应用［M］.北京:科学出版社，2008.WANG Zhiping，WANG Zhongtuo.Theory and application of hypergraphs［M］.Beijing:Science Press，2008.(in Chinese)

［12］周晓宇，刘四海.联合作战协同简论［M］.北京:国防大学出版社，2007.ZHOU Xiaoyu，LIU Sihai.Brief introduction to coordination in jointoperation［M］.Beijing:National Defense University Press，2007.(in Chinese)