数控振荡器相位截断对频域抗干扰性能影响分析*

李 建，聂俊伟，李柏渝，王飞雪

(国防科技大学电子科学与工程学院，湖南长沙410073)

全球导航卫星系统(Global Navigation Satellite System，GNSS)具有大范围、全天候、高精度定位、测速和定时服务能力，在国防和国民经济等各个领域得到广泛的应用［1］。然而，由于到达地面的卫星信号极其微弱，GNSS接收机非常容易受到各种无意、有意干扰的影响，严重的可能导致接收机无法工作［2］。因此，在GNSS接收机中加入抗干扰措施就显得迫切而重要。

经过多年的研究，国内外学者在抗干扰领域取得丰硕的成果。学术界发表了大量GNSS抗干扰方面的文章，方法涉及与时域、频域、空域、空时和极化等特性相关的抗干扰技术以及多径消除等问题［3-13］。频域抗干扰算法因其窄带干扰抑制效果好、易于工程实现，被广泛应用于抗干扰接收机中［14］。

目前，频域抗干扰算法的理论研究已非常成熟，然而频域抗干扰算法在实际的运用中仍然存在一些问题。通常抗干扰接收机中的数字混频采用免混频方式，此时输出的本振信号只用2bit表示即可满足性能要求［15］。但受整个频率规划影响无法采用免混频方式时，需要使用数控振荡器(Numerically Controlled Oscillator，NCO)。在频域抗干扰算法的硬件实现时发现，NCO的地址查找表(Look Up Table，LUT)位宽大小对频域抗干扰性能影响很大。关于数字NCO的相位截断效应的理论研究很多，大多集中在NCO相位截断导致输出信号产生杂散的机理分析和杂散抑制上［16-18］，几乎没有关于NCO相位截断对频域抗干扰性能影响的研究。

1 NCO相位截断

NCO的实现方式如图1所示。

图1 NCO实现示意图Fig.1 Structure of NCO

NCO相位累加器输出的结果无法直接生成正/余弦信号，需要通过LUT将相位累加结果转换为幅度值输出。在现场可编辑门阵列(Field Programmable Gate Array，FPGA)实现时，通常需要取位宽L(典型值为32 bit)的相位累加结果的高W(典型值为3 bit)位作为LUT的地址，该处理即所谓的相位截断处理。相位截断带来的最大影响是引入杂散分量。杂散频率位置由式(1)决定［17］。

其中，fout为期望合成频率，B=L-W。最大杂散位置为

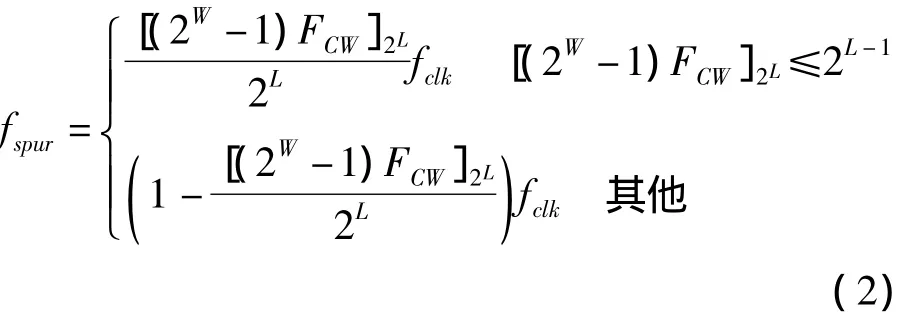
其中，［·］2L代表对2L取余。理想的载波与最大杂散幅度比为

L〉W+4，式(3)近似为6.02WdBc。通常L≫W，由此可见LUT的地址字长W提高1位能带来6.02dB的无杂散动态范围(Spurious Free Dynamics Range，SFDR)的提高。

2 数字混频

NCO通常位于抗干扰接收机的数字混频模块中。图2为典型的数字混频模块组成示意图［19］。

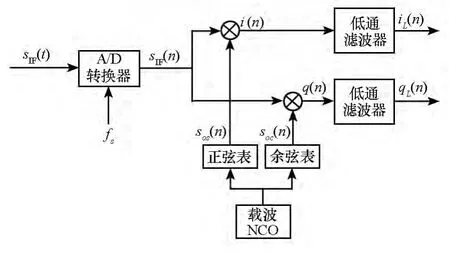
图2 数字混频示意图Fig.2 Structure of digital frequency mixer

来自射频前端输出的模拟中频信号经过模数(Analog/Digital，A/D)转换采样成为数字中频信号sIF(n)，sIF(n)经过与NCO生成的本振信号混频得到下变频信号

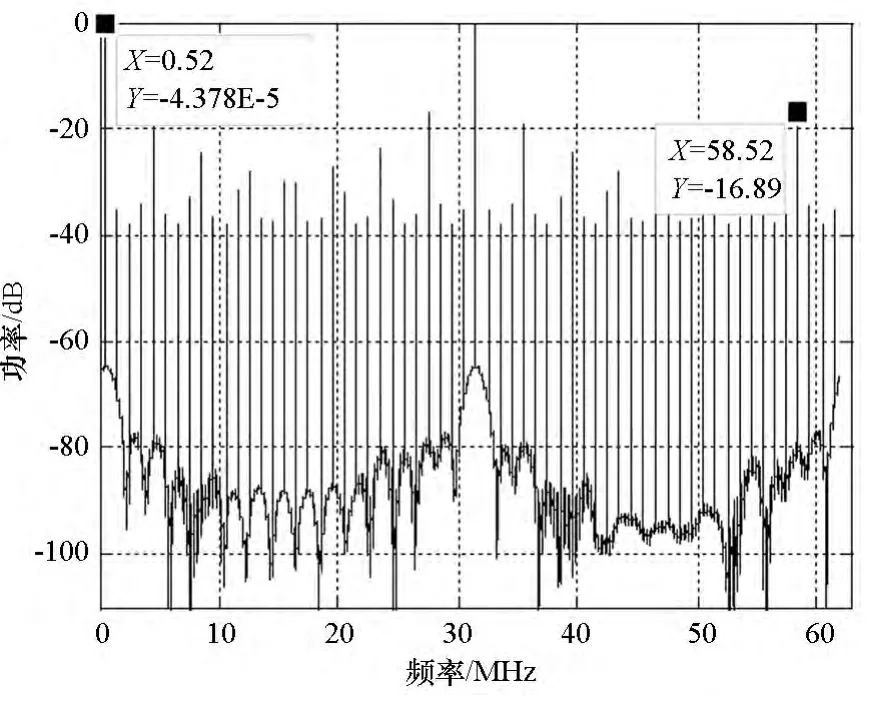
图3 混频后信号频谱图Fig.3 Spectrum of signal after frequency mixing

其中:T为采样间隔，wl为本振生成的不同频率分量，Al为其幅度;SIF(K)为中频信号频域表达式，分别为Alsin(nTwl)和Alcos(nTwl)的频域表达式。由此可见，NCO产生的信号产生杂散分量，经过图2中的数字混频，sIF(n)中的干扰信号经过频域卷积会被调制到NCO产生的各个杂散分量上，混频后信号的频谱如图3所示。图3中干扰的载波为46.52MHz，采样频率为62MHz，本振频率为46MHz。由图3可知，除了46.52MHz与46MHz混频产生的0.52MHz的干扰主分量外，还存在包括46.52MHz与最大杂散分量50MHz混频产生的58.52MHz在内的杂散干扰。

由上述分析可知，NCO引入的杂散分量，导致干扰信号在混频后生成许多杂散干扰。假设主干扰强度为80dBc，根据式(3)得杂散干扰最大功率，如图4所示。

图4 不同LUT位宽下的最大杂散干扰功率Fig.4 Maximum spur power at different LUT width

由图4可知，LUT地址位宽取3bit时，最大杂散干扰的干信比将高达60dBc，仅与主干扰相差20dB。此外，观察图3可知，除了最大杂散干扰外还存在许多功率与其相近的杂散干扰。综上，NCO相位截断产生的本振杂散经过与输入中频信号混频，会引入额外的杂散干扰。

3 杂散干扰对频域抗干扰影响

在讨论杂散干扰对频域抗干扰性能影响之前，首先简单描述频域抗干扰的处理流程。频域抗干扰的实现方法主要有重叠选择法和重叠相加法，文献［20］指出1/2重叠相加法的信噪比损耗更小。因此，选择1/2重叠相加的频域抗干扰方法。不同的时域窗导致的信噪比损耗存在差异。由文献［20］可知，采用汉明窗时，1/2重叠相加处理引入的信噪比损耗接近0。故采用汉明窗进行加权处理。频域抗干扰的关键环节在于干扰抑制。工程中通常采用门限归零法(Threshold Zero，TZ)，即根据噪声的功率谱，求得一个门限值Th，将幅度超过该门限的谱线归零。其公式可表述为

频域加权阈值为

Th为干扰检测的门限，工程中通常采用固定门限，门限的获取根据下述推导得来。通常认为卫星信道为恒参信道，进入接收机的噪声功率近似恒定。假设噪声是均值为0、方差为σ2的高斯噪声，则经过线性变换快速傅里叶变换(Fast Fourier Transform，FFT)后，其频谱仍然服从高斯分布，其方差

由Parseval定理可知:

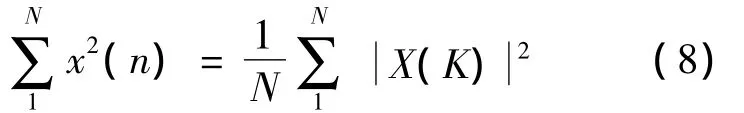
N为FFT点数，则

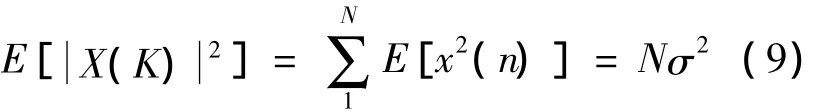
可知，X(K)的方差，其幅度谱服从瑞利分布。由于P{X(K)〈，故通常以3即3即3作为阈值Th。由于信号加窗会导致信噪比的损耗，故需要对上述阈值做如下的修正:［20］

图5给出NCO的LUT取4bit时，带宽为1MHz、干信比为80dBc的窄带干扰与噪声、导航信号混合信号混频后的频谱，图5中的阈值根据式(10)计算得到。由图5可知，超过阈值的谱线带宽接近10MHz，接近导航信号的一半带宽。也就是说将有10MHz左右的导航信号谱线被置零，这将导致极大的载噪比损耗，甚至导致载噪比估计失效。NCO相位截断引入的杂散干扰使得窄带干扰的抑制转化为宽带干扰的抑制。

为了更好描述LUT的位数选取不合理导致的额外信噪比损耗，上述条件不变，LUT的位宽分别取10～4bit，步进为1bit。以NCO相位不截断的载噪比损耗作为基准，LUT位宽减小引入的载噪比损耗见表1。表1表明，若LUT位宽选取不合理，NCO截断效应将额外引入最大6.9dB的载噪比损耗。

表1 不同LUT位宽下载噪比损耗Tab.1 CNR loss at different LUT width

图5 混频后信号频谱Fig.5 Spectrum of signal after frequency mixing

下面从理论分析使用频域抗干扰抑制部分频带干扰引入的载噪比损耗。如图5所示，窄带干扰主分量及杂散干扰的中心频率虽然可由式(1)计算得到，但其分布散乱难以从理论上分析载噪比损耗。故此处将NCO相位截断导致的抗干扰置零带宽增加近似等效为一个理想部分频带干扰的带宽增加。以此近似分析NCO相位截断导致的抗干扰损耗。设部分频带干扰为高斯干扰，其功率谱为理想的矩形，干扰谱线抑制完全，则干扰抑制后的载噪比为

其中，CS为导航信号的主瓣能量，Closs为频域抗干扰引入的导航信号能量的损失，噪声带宽B在工程中通常取伪码的主瓣带宽即2Rc。故采用二进制相位调制(Binary Phase Shift Keying，BPSK)调制的导航信号，频域抗干扰引入的载噪比损耗为

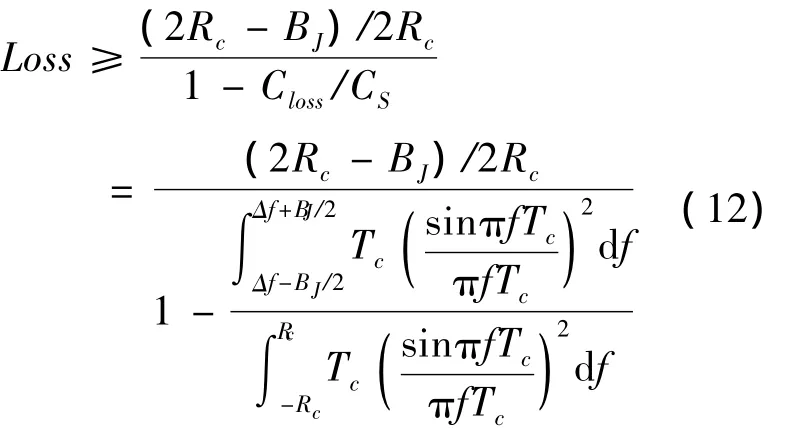
伪码速率Rc取10.23Mcps，Tc与Rc互为倒数，BJ为干扰带宽，干扰与导航信号频偏Δf取0，即干扰载波与导航信号中心频率重合。图6给出窄带干扰带宽与频域抗干扰损耗关系。由图6可知，随着干扰带宽的增加，频域抗干扰引入的载噪比损耗随之增加。抑制带宽10MHz的宽带干扰将比抑制带宽1MHz的窄带干扰多损失5dB的载噪比。这里仅是理想条件下的分析，认为干扰谱线被完全抑制，考虑到实际环境下功率谱估计的误差、FFT处理时的频谱泄漏等因素，载噪比损耗还将更大。由此可见，NCO相位截断引入的杂散干扰将引起额外的抗干扰损耗。此外，频谱中还残余大量未超过抗干扰阈值的杂散干扰未被抑制，它们会引起载噪比的进一步下降。综上，NCO的LUT位宽过小，将影响干扰在频域的能量聚焦，引入额外的抗干扰损耗和噪底抬升。

图6 窄带干扰带宽与频域抗干扰损耗关系Fig.6 Band of interference versus frequency domain anti-jamming loss

4 合理的NCO字长设置

上述章节分析了NCO相位截断导致的载噪比恶化，这节将讨论如何解决该问题。NCO的相位截断效应削弱方法较多，有相位抖动法、泰勒修正法和提高只读内存(Read-Only Memory，ROM)存储容量法(即增加LUT地址位宽数)［21］。在工程中，最简单的方法即适当地增加LUT的位宽。受FPGA资源限制，LUT的位宽不能任意增加，需要既满足抗干扰性能又能保证硬件容易实现。这里采用如下标准选取合理的LUT位宽:LUT位宽保证最大杂散干扰的谱线不超过功率谱噪声方差，即保证杂散干扰淹没在噪声中。假设窄带干扰的功率谱为理想矩形，即满足

将式(3)带入式(14)即得到抗干扰性能接近NCO无相位截断时的LUT最小位宽Wmin。

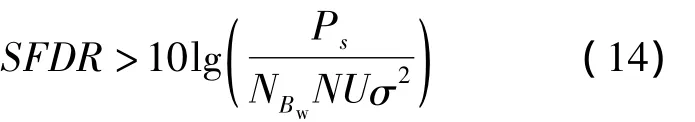
5 仿真实验

为验证上述方法，在软件接收机中做对比实验。软件接收机的处理流程如图7所示。

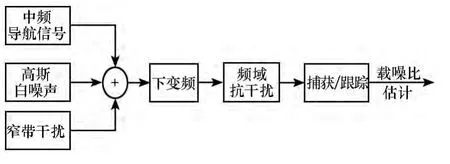
图7 软件接收机处理流程Fig.7 Flow diagram of soft receiver

软件接收机下变频的本振为46MHz，工作时钟为62MHz，带宽为62/3MHz，NCO的相位累加字长L取32bit。频域抗干扰模块的时域窗为汉明窗，FFT的点数N为2048。实验条件设置如下:导航信号的伪码速率为10.23Mcps，中频载波为46.52MHz，采样频率为62MHz，载噪比为50dBHz。噪声采用均值为0、方差为1的高斯白噪声。干扰分别采用带宽为100kHz，500kHz和1MHz的高斯窄带干扰。干扰的干信比从60dBc取至80dBc，步进为5dB。

将干扰的干信比转化为干扰功率带入式(14)，计算得到满足要求的最小NCO位宽Wmin，表2给出了不同条件下满足要求的最小位宽Wmin。由表2可知，不同带宽、干信比下的最小位宽Wmin最大不超过10bit，现有FPGA资源很容易满足。注意到，干扰功率相等的条件下，干扰带宽越小Wmin越大。原因在于，根据式(14)计算Wmin时，同样功率的干扰，带宽越宽，干扰谱线幅度越小，Wmin越小。在软件接收机中将NCO的LUT位宽设置为Wmin，做100次蒙特卡洛实验，估计载噪比。为做对比，其他实验条件不变，NCO相位不截断做100次蒙特卡洛实验，估计载噪比。

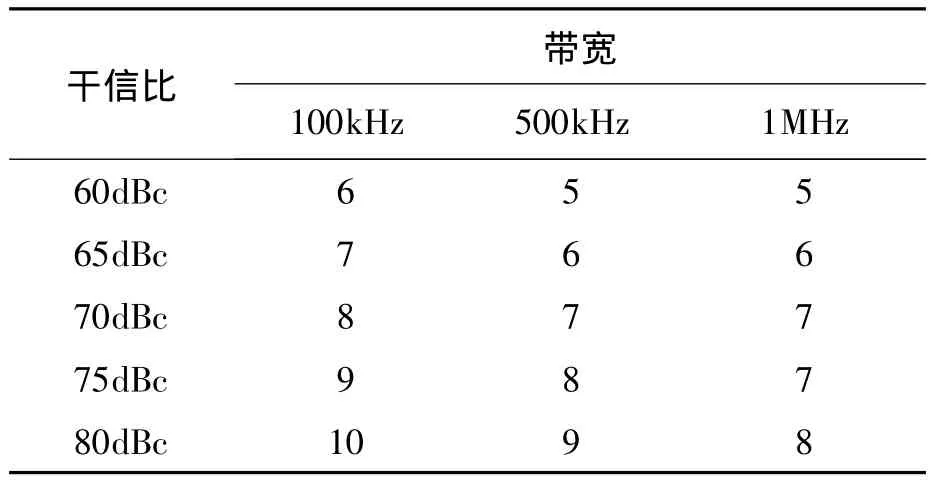
表2 不同带宽窄带干扰下的最小位宽WminTab.2 Wmin at different interference band bit

表3给出了不同LUT位宽W下的载噪比估计结果。由表3可知，其他条件相同，干扰带宽越大，载噪比损耗越大。这是因为干扰带宽越大，抗干扰损耗越大。其他条件相同，干扰功率越大，载噪比损耗越大。这是因为，干扰功率越大，功率谱泄漏越严重，干扰抑制时置零谱线越多，抗干扰损耗越大。此外，由表3可知，采用该理论模型计算的Wmin作为NCO的LUT位宽时，频域抗干扰后的载噪比与NCO无相位截断(W=L)时的载噪比相近，最大相差0.6dB。而若直接将NCO的LUT位宽W设置为4bit，随着窄带干扰带宽和干信比的增加，频域抗干扰后的损耗逐渐增大，与无相位截断条件的相比，其载噪比最大相差6.9dB。

表3 不同LUT位宽W下的载噪比估计结果Tab.3 CNR estimated at different LUT W dB

综上，采用该计算模型能够在抗干扰性能和节约硬件资源上取得较好的平衡。在实际应用时，无法预知干扰的功率和带宽，建议根据干扰抑制度指标和FFT的频率分辨率(作为干扰带宽)计算最大的Wmin，以适应所有带宽的窄带干扰。

6 结论

在阐述NCO相位截断导致的本振杂散基础上，本文详细分析NCO的相位截断对频域抗干扰性能的影响。针对采用固定门限的TZ法的频域抗干扰接收机，给出抗干扰损耗接近NCO无相位截断时的最小LUT位宽Wmin的理论计算模型。仿真结果表明:抑制带宽大于100kHz、干信比小于80dBc的窄带干扰时，理论模型得到的Wmin小于10bit，现有FPGA资源下很容易实现。与NCO无相位截断时相比，若W=Wmin，载噪比损耗最多增加0.6dB;而若W=4bit，载噪比损耗最多增加6.9dB。

References)

［1］干国强，邱致和.导航与定位:现代战争的北斗星［M］.北京:国防工业出版社，2002.GAN Guoqiang，QIU Zhihe.Navigation and location:the big dipper of modern warfare［M］.Beijing:National Defense Industry Press，2002.(in Chinese)

［2］Johannessen R，Cole S J，Asbury M J A.Potential interference sources to GPS and solutions appropriate for applications to civil aviation［J］.IEEE Aerospace and Electronic Systems Magazine，1990，5(1):3-9.

［3］Li Q，Wang W，Xu D J，et al.A robust anti-jamming navigation receiver with antenna array and GPS/SINS［J］.IEEE Communications Letters，2014，18(3):467-470.

［4］曾祥华，李敏，聂俊伟，等.卫星导航系统中平台运动对天线阵列性能的影响分析［J］.国防科技大学学报，2011，33(1):95-99.ZENG Xianghua，LI Min，NIE Junwei，et al.Effects of motion on adaptive array in satellite navigation systems［J］.Journal of National University of Defence Technology，2011，33(1):95-99.(in Chinese)

［5］Amin M G，Sun W.A novel interference suppression scheme for global navigation satellite systems using antenna array［J］.IEEE Journal on Selected Areas in Communications，2005，23(5):999-1012.

［6］Qiu B，Liu W，Wu R B.Blind interference suppression for satellite navigation signals based on antenna arrays［C］//Proceedings of China Summit and International Conference on Signal and Information Processing(China SIP)，Beijing，2013.

［7］Gardner W A.Cyclic wiener filtering theory and method［J］.IEEE Transactions on Communications，1993，41(1):151-163.

［8］孙志国.直扩通信系统中窄带干扰自适应抑制算法的研究［D］.哈尔滨:哈尔滨工程大学，2005.SUN Zhiguo.Research on adaptive narrow band interference suppression algorithm in direct spread spectrum communication system［D］.Harbin:Harbin Engineering University，2005.(in Chinese)

［9］Young J A，Lehnert J S.Analysis of DFT-based frequency excision algorithms for direct-sequence spread-spectrum communications［J］.IEEE Transactions on Communications，1998，46(8):1076-1087.

［10］李冲泥，胡光锐.一种新的重叠变换域抗窄带干扰技术［J］.电子学报，2000，28(1):117-119.LI Chongni，HU Guangrui.A new lapped transform domain narrow-band interference excision technique［J］.Acta Electronica Sinica，2000，28(1):117-119.(in Chinese)

［11］Li M，Dempster A G，Balaei A T，et al.Switchable beam steering/null steering algorithm for CW interference mitigation in GPS C/A code receivers［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47(3):1564-1579.

［12］Melvin W L.A STAP overview［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，19(1):19-35.

［13］Wang Y C，Milstein L B.Rejection of multiple narrow-band interference in both BPSK and QPSK direct-sequence spreadspectrum systems［J］.IEEE Transations on Communications，1988，36(2):195-204.

［14］Ojeda O A Y，Grajal J，Lopez-Risueno G.Analytical performance of GNSS receivers using interference mitigation techniques［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49(2):885-906.

［15］Mitora J.The software radio architecture［J］.IEEE Communications Magazine，1995，33(5):26-38.

［16］Wang G P.An FPGA-based spur-reduced numerically controlled oscillator［C］//Proceedings of International Conference on System Science and Engineering，Dalian，2012:187-192.

［17］Curticapean E，Niittylahti J.Exact analysis of spurious signals in direct digital frequency synthesisers due to phase truncation［J］.Eclectronics Letters，2003，39(6):499-501.

［18］Kroupa V F，Cizek V，Stursa J，et al.Spurious signals in direct digital frequency synthesizers due to the phase truncation［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2000，47(5):1166-1172.

［19］谢钢.GPS原理与接收机设计［M］.北京:电子工业出版社，2009.XIE Gang.Principles of GPS and receiver design［M］.Beijing:Publishing House of Electronics Industry，2009.(in Chinese)

［20］曾祥华，李峥嵘，王飞雪.扩频系统频域窄带干扰抑制算法加窗损耗研究［J］.电子与信息学报，2004，26(8):1276-1281.ZENG Xianghua，LI Zhengrong，WANG Feixue.Study on windowing degradation of frequency-domain narrowband interference suppression algorithms in spread spectrum system［J］.Journal of Electronics＆Information Technology，2004，26(8):1276-1281.(in Chinese)

［21］俞麒.基于改进算法的NCO杂散抑制实现［J］.中国科技信息，2009，2:37-38.YU Qi.Implementation of the spur suppression of NCO based on improved algorithm［J］.China Science and Technology Information，2009，2:37-38.(in Chinese)