机械结构实验模态分析及典型应用

黄 捷，季 忠，段虎明，秦树人

（重庆大学机械工程学院测试中心，重庆 400030）

1 引 言

模态分析是研究结构动力特性的一种近代方法，是系统辨别方法在工程振动领域中的重要应用。模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得，这个分析过程称为模态分析。如果通过模态分析方法搞清楚了结构物在某一易受影响的频率范围内各阶主要模态的特性，就可能预言结构在此频段内在外部或内部各种振源作用下实际振动响应。因此，模态分析是结构动态设计及设备的故障诊断的重要方法[1-5]。

2 模态分析的基本原理

工程实际中的振动系统都是连续弹性体，理论上它们都属于无限多自由度的系统，需要用连续模型才能加以描述。但实际上通常采用简化的方法把系统归结为有限个自由度的模型来进行分析，即将系统抽象为由一些集中质块和弹性元件组成的模型。如果简化的系统模型中有n个集中质量，一般它便是一个n自由度的系统，需要n个独立坐标来描述它们的运动，系统的运动方程是n个二阶互相耦合（联立）的常微分方程[6]。

一个结构的动态特性可由N阶矩阵微分方程描述[2]：

式中：f（t）——N维激振力向量；

M、C、K——结构的质量、阻尼和刚度矩阵，通常为实对称N阶矩阵。

设系统的初始状态为零，对方程式（1）两边进行拉普拉斯变换，可以得到以复数s为变量的矩阵代数方程：

式中 Z（s）=［M s2+Cs+K ］，反映了系统的动态特性，称为系统动态矩阵或广义阻抗矩阵。其逆阵:

称为广义导纳矩阵，也就是传递函数矩阵。由式（2）可知：

在该式中令s=jw，即可得到系统在频域中输出（响应向量 X（ω））和输入（激振向量 F（ω））的关系式：

式中H（ω）为频率响应函数矩阵。H（ω）矩阵中第i行第j列的元素：

等于仅在j坐标激振（其余坐标激振力为零）时，i坐标响应与激振力之比。

在式（3）中令s=jw，可得传递函数矩阵：

利用实对称矩阵的加权正交性，进行一系列公式推导，得到：

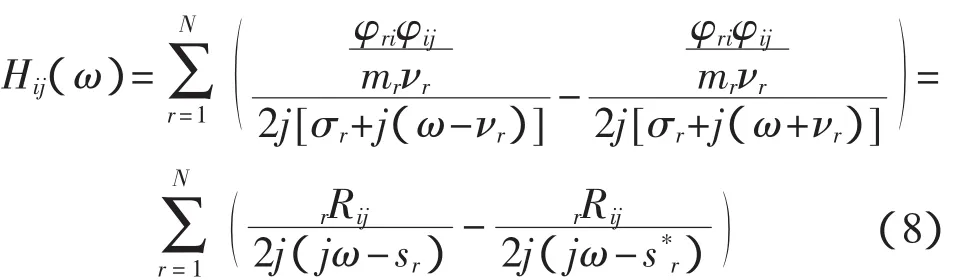
sr=σr+jνr——第r阶极点，上标星号表示复共轭。

sr与 ωr、ξr的关系为：

mr、kr、cr——第r阶模态质量、模态刚度和模态阻尼；

φri——第r阶模态振型。

相应地，将上式的频响函数做Fourier反变换可以得到时域的脉冲响应函数表达式为：

频响函数矩阵还可以写成多种表达形式，分别表示幅相频关系、实虚频关系和矢量图形式，依据这些表达形式可绘制出相应的特性曲线。这些曲线为实验模态参数的识别提供依据。

实验模态分析或模态参数识别的任务就是由一定频段内的实测频率响应函数数据，确定系统的模态参数——固有频率ωr、模态阻尼比ξr和振型φr=（φr1，φr2，L，φrN）T，r=1，2，L，N（这里可以认为 N 是系统在测试频段内的模态数）[7]。

3 简支梁实验模态分析

3.1 简支梁的结构及实验装置

如图1（a）所示为简支梁实验装置图，在图中实验台上正中间是一根简支梁，现在对其进行模态实验。该简支梁长（x向）600 mm，宽（y向）50 mm，高（z向）8mm。由于简支梁在y、z方向尺寸和x方向（尺寸）相差较大，故可以简化为杆件结构。图1（b）中QLV-MA2型模态分析仪是重庆大学测试中心自主研发的一体化虚拟式模态分析仪。

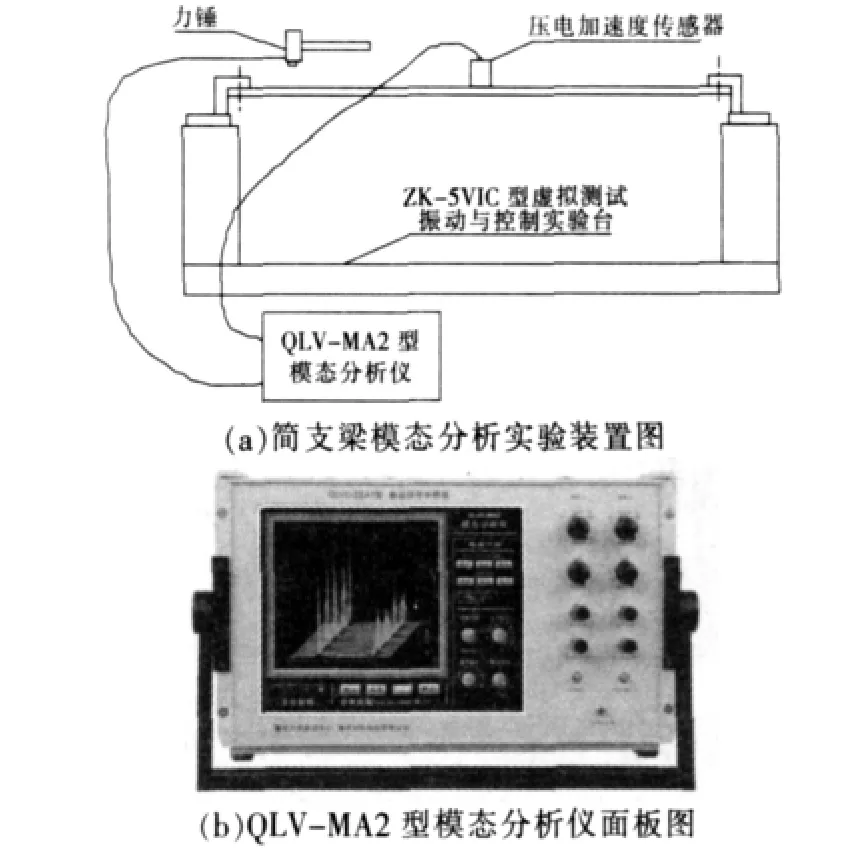
图1

3.2 简支梁测点的布置

实验中在x方向把梁等分成16等份，即可以布17个测点。选取拾振点时要尽量避免拾振点在模态振型的节点上，该实验取拾振点为第6个敲击点处，网格划分图如图2所示。根据简支梁的结构，在x方向顺序布置若干敲击点，并采用多点敲击、单点定点响应方法，在z方向使用力锤进行锤击实验。

图2 简支梁测点布置图

3.3 简支梁频响函数的求取

试验模态分析主要分析结构的振动，简单而言，就是在结构上安装传感器，通过对结构进行激振试验测定激励和响应信号，分别为f（t）和x（t），经FFT变换后得到频域信号F（ω）和X（ω），由此可以得到结构的频响函数，如式（11）所示：

使用QLV-MA2型模态分析仪及图所示的实验装置采集各测点各方向的激励和响应信号。如图3（a）所示简支梁上激励点编号为3，激励方向为Z方向的时域曲线图形（上面为冲激信号，下面为响应信号）；图3（b）所示为该点该方向对应的频域曲线图形。当采集完当前测点当前方向的数据之后，根据公式（11）即可计算出该测点该方向的频响函数。如图3（c）所示为该点该方向的频响函数曲线，图3（d）所示为该测点该方向对应的相干函数曲线。

3.4 简支梁模态参数的识别

求得各测点各方向的频响函数之后，就根据这些频响函数数据来确定系统的模态参数——固有频率ωr、模态阻尼比ξr和振型φr=（φr1，φr2，L，φrN）T，r=1，2，L，N，（这里 N 可以认为是系统在测试频段内的模态数）。

模态参数识别的方法有很多种。频域模态参数识别法是目前各类模态试验中使用最为广泛的方法。频域模态参数识别法中比较流行的是整体正交多项式曲线拟合法，可以胜任多种结构的模态试验的任务。主要采用正交多项式法来识别模态参数。在QLV-MA2型模态分析仪采集部分采集完所有测点所有方向的数据并且计算完各测点各方向的频响函数之后，下步需要进行参数拟合。在频响函数的叠谱或者均值谱的状态下，可以通过单点或者整体按钮来进行单点曲线拟合或者整体曲线拟合。

如图4（a）所示为简支梁频响函数的幅值谱阵，图4（b）所示为为简支梁频响函数的幅值叠谱（Y轴为dB坐标模式），图4（c）所示为简支梁频响函数的幅值频谱的均值谱阵。通过图4（b）或者图4（c）可以明显的看出有4阶模态，选定峰值和拟合区间的叠加频谱图如图 4（d）所示。

3.5 简支梁模态输出

在使用整体有理正交多项式方法对简支梁进行模态参数识别之后，就可以进行模态参数输出、模态振型的演示以及模态验证。这部分的工作在QLV-MA2型模态分析仪的输出部分完成。该简支梁的前4阶振型如图5所示，模态参数识别结果参数如表1所示。

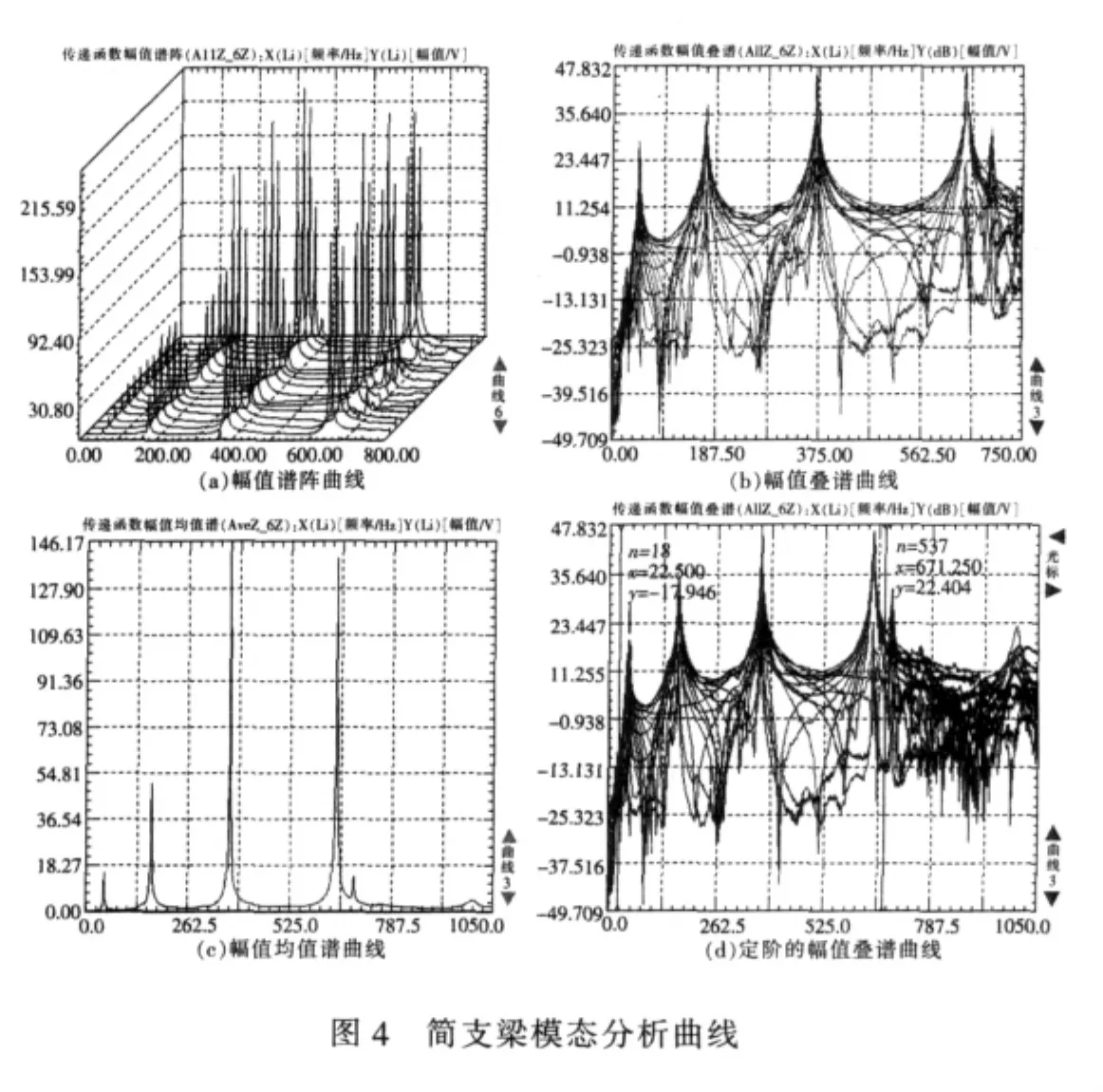
表1中QLV-MA2列表示是使用重庆大学测试中心的QLV-MA2型虚拟式模态分析仪计算的结果，DASP列表示是使用东方振动噪声研究所的DASP模态分析软件计算的结果，可见两者精度上没有什么差别，分析计算结果与理论结果不符（偏小）的原因应该是加速度传感器附加在简支梁上面，相当于给简支梁增加了附加质量，所以计算出的固有模态就应该偏小。

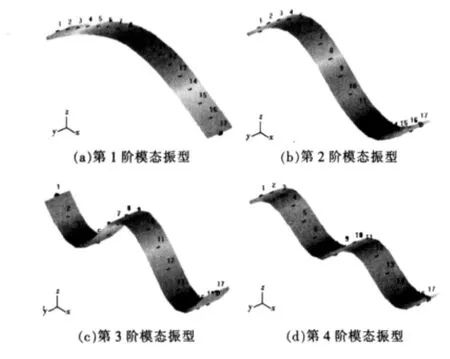
图5 简支梁第1到4阶模态振型曲线

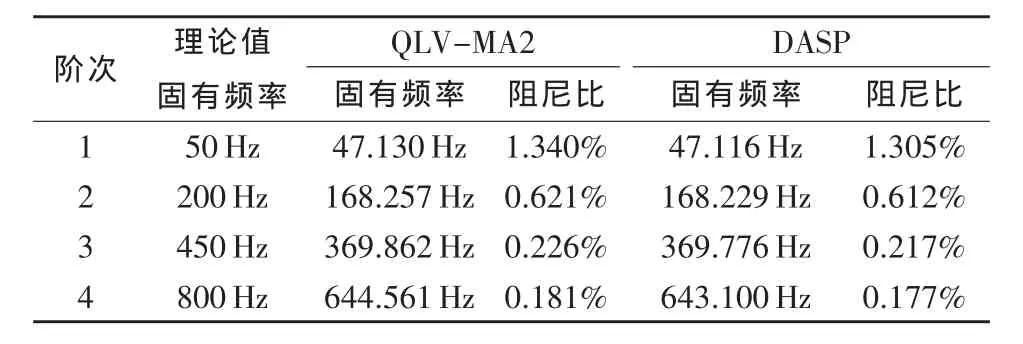
表1 简支梁的模态参数

4 摩托车车架实验模态分析

4.1 摩托车车架结构及测点布置

如图6所示为摩托车车架结构。该框架是一个摩托车的主干框架结构，将其上的所有附件拆除以后，使用柔软的弹簧悬挂，近似作为自由状态进行模态实验分析。

图6 摩托车车架结构

该车架为一个形状较复杂的结构，长约为1.2m，宽约为0.35 m，高约为0.5 m，其主干件为圆筒形钢管。根据该摩托车车架的具体尺寸对其进行单元划分和结点布置，根据其截面相对大小，在其上布置34个测点，以梁单元（杆单元）为主，夹杂一些三角形单元和四边形单元。具体的单元格划分和测试点的布置如图7所示。考虑到数据采集量比较大，为了实验进度，仅对Y轴（垂直方向）和Z轴（水平宽度方向）方向的部分结点进行了测量。采用定点响应（响应测试点为测点7的Y轴方向），力锤移步敲击所有其他测试点的Y轴方向或者Z轴方向，进行数据采集。

4.2 摩托车车架频响函数求取及模态参数识别

在完成所有34个测点的数据采集以后，就可以使用这些数据进行频响函数的估计。如图8所示为测点7方向Y的时域和频域曲线。根据式（11）来求取所有测点和所有方向的频响函数。

在完成频响函数的计算之后，需要进行参数拟合。在频响函数的叠谱或均值谱的状态下，可通过单点或整体来进行曲线拟合。计算结果频响函数的幅值均值谱阵如图9（a）所示，图9（b）为定阶后的幅值均值谱曲线。

4.3 摩托车车架结构模态输出

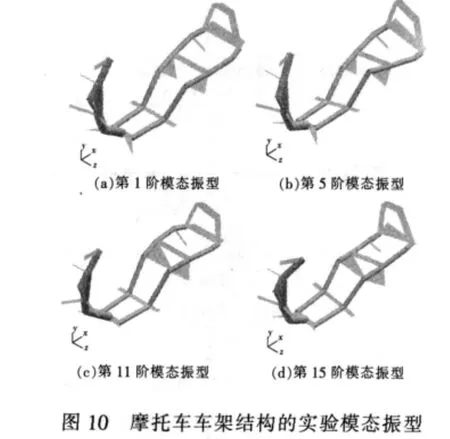
根据图9（b）进行拟合区间和峰值确定以后，应用整体有理正交多项式模态参数识别方法，对该车架结构的模态参数进行识别。识别结果振型如图10所示。该车架结构的模态参数实验识别结果和计算模态参数结果如表2所示。

表2中QLV-MA2列表示使用重庆大学测试中心的虚拟式模态分析仪的测试分析结果。从各阶的模态参数和各阶振型可以看出，实验数据通过QLV-MA2软件识别结果与结构本身的振动情况基本上是一致的，这样的计算结果达到一般工程测量和计算的要求。

表2 车架结构的模态参数

5 结束语

通过对简支梁和摩托车车架的实验模态分析结果表明，模态分析方法通过QLV-MA2型一体化模态分析仪在机械结构中的应用是有效可行的。从实验结果的模态振型上看，QLV-MA2型一体化虚拟式模态分析仪识别的结果，与结构本身的振动情况是一致的；与其他的商业模态软件的结果比较，精度上没有大的差别。从实验结果的模态参数上看，基本与使用有限元仿真计算结果存在着比较小的误差，但是总体上是一致的。显然，这样的计算结果已经达到一般工程测量和计算的要求。

[1]曹树谦，张文德.振动结构模态分析——理论、实验与应用[M].天津：天津大学出版社，2001.

[2] 李德葆，陆秋海.实验模态分析及其应用[M].北京：科学出版社，2001.

[3]Heylen W，Lammens S，Sas P.实验模态分析理论与试验[M].白化同，郭继忠译.北京：北京理工大学出版社，2001.

[4] 傅志方，华宏星.模态分析理论与应用[M].上海：上海交通大学出版社，2000.

[5] 傅志方，华宏星.模态分析的概念和发展历史[EB/01].http：//dengyuehua.blogchina.com/dengyuehua1973/4790467.html，2006-04-02.

[6] 张 策.机械动力学[M].北京：高等教育出版社，2008.

[7]段虎明.实验模态分析的前端信号精度研究及虚拟式模态分析仪的研制[D].重庆：重庆大学，2008.