分布式二进制传感器网络目标定位研究*
刘 忠,罗 浩,任雄伟,彭鹏菲
(海军工程大学电子工程学院,湖北 武汉 430033)
无线传感器网络[1](WSN)是当前国际上备受关注、由多学科高度交叉的新兴前沿研究热点领域。目标定位与跟踪是WSN的一项重要应用。二进制临近传感器[2,3]因其价格低廉、能提供最基本的感知能力(只能提供关于目标是否在其感知范围内的1比特信息),可以大量部署在监测区域对目标实施定位跟踪。
在分布式二进制传感器网络中,由于没有严格的控制中心,所有节点地位平等,是一个对等式网络。由于单个节点单独对目标进行定位会带来很大的误差,需要多个节点协同对目标进行定位,因此跟踪系统中,节点的协作和目标定位算法成为两个关键环节。现有的基于动态簇的节点协作方法[4,5],因为簇的组建、簇头对簇结构的管理、簇的重组等需要耗费节点大量的能量,且常存在丢失目标和簇头电量耗尽的风险。文献[4]和[5]的分簇方法并不是专门针对二进制传感器网络的,不能直接使用。文献[6]所采用的“邻居节点状态表”与本文所用到的邻居节点状态表相似,但其所指邻居的概念不同。本文所指的邻居是指某节点通信距离范围内所有节点的集合,文献[6]中所指的邻居是指探测区域与该节点探测区域相交的所有节点的集合(实际应用中,较难获取)。因此,本文提出了一种简单的协作方法,通过传感器检测到的特定事件(目标进入或目标离开)触发节点发送协作消息和完成对目标的定位,节点收到消息后对邻居节点状态表进行更新。
文献[7]和[8]提出的粒子滤波算法之所以不适用于分布式二进制传感器网络,是因为粒子滤波计算复杂度高、实时性差,不适用传感器节点级别的处理;文献[2]和[3]提出的改进质心算法,需要节点时间同步,因而对节点硬件和能量要求较高;而常用的质心定位算法定位精度又太低,满足不了某些场合的应用需求;文献[6]提出的求弧中点的定位方法计算复杂、不易实现。因此,本文提出了一种基于m-网格的定位算法,主要研究了分布式二进制传感器网络对单目标进行定位的情况,其定位原理简单、易于实现,计算复杂度可调节(通过控制m的大小),定位精度优于质心定位法。
1 网络模型
分布式二进制传感器网络由N个二进制临近传感器节点组成,以随机的方式均匀部署在监视区域内,节点部署后不移动,如图1所示。节点通过全球定位系统(GPS)、有向天线或定位算法等辅助设施和算法。可以获知其位置信息,二进制临近传感器只有两种探测状态,即它只能判断目标处于节点探测区域之内或者之外。为了使问题简单化,文中假设所有的传感器节点具有相同的探测半径。特别地,本文传感器节点能够检测出前后两个时刻的探测状态是否相同,即传感器节点能够检测到目标进入或离开传感器的探测区域。
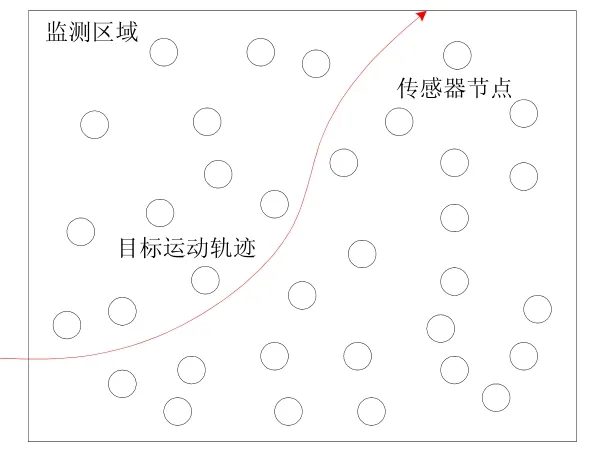
图1 用于目标跟踪的二进制传感器网络
2 简单协作方法
简单协作方法描述如下:每个节点负责维护一张邻居节点状态表,表的每条记录包括邻居节点编号、位置、状态(表明是否探测到目标)。传感器节点部署后,节点通过相互发送“Hello消息”,可以获取邻居节点编号、位置;状态初始统一设置为“0”(表明没有探测到目标)。当节点检测到目标进入或离开传感器节点的探测区域时,本地广播(单跳)一个目标进入消息或目标离开消息。收到“目标进入消息”或“目标离开消息”的节点对其邻居节点状态表进行更新。更新的规则如下:如果收到的是“目标进入消息”,从该消息中可以提取发送该消息的节点编号,在邻居节点表中查找到该节点编号的记录,将记录中的状态属性更新为“1”;如果收到的是“目标离开消息”,从该消息中可以提取发送该消息的节点编号,在邻居节点表中查找到该节点编号的记录,将记录中的状态属性更新为“0”。各协作消息的定义见表1。并规定:节点仅当探测到目标进入或目标离开传感器探测区域时,利用邻居节点状态表提供的信息对目标进行定位,并将定位结果发送给远方基站,由基站采用跟踪算法对定位点序列进行处理。

表1 协作消息定义
从以上描述可以看出,当目标在传感器网络监视区域运动时,只有节点检测到目标进入或离开它的探测区域时,它才会单跳广播“目标进入消息”或“目标离开消息”,因此通信量很小。
3 基于m-网格的定位算法
当节点检测到目标进入或离开其传感器探测区域时,它利用邻居节点状态表提供的信息对目标进行定位。通过邻居节点状态表,节点可以知道当前自己的邻居节点是否探测到目标。最简单的定位方法是常用的质心定位法,它是取所有探测到目标的节点位置的均值作为对目标位置的估计。
与该方法不同,我们提出了一种基于m-网格的定位方法,该方法考虑到了未探测到目标的邻居节点对定位所作的贡献。其主要思想是:先确定一个包括目标可能存在位置的矩形区域,然后将该区域划分m个网格(m=n2,n为自然数),确定这些网格中心点(网格点)的坐标,选出满足一定条件的网格点,以这些网格点坐标的均值作为对目标位置的估计。如图2所示,节点3检测到目标进入,搜索邻居节点表发现节点1和节点2也探测到目标,而节点4未探测到目标,先通过节点1、节点2和节点3的位置确定图中的矩形区域,然后对矩形区域进行网格化,找到阴影区域内的网格对应的网格点,以这些网格点位置的均值作为对目标位置的估计。
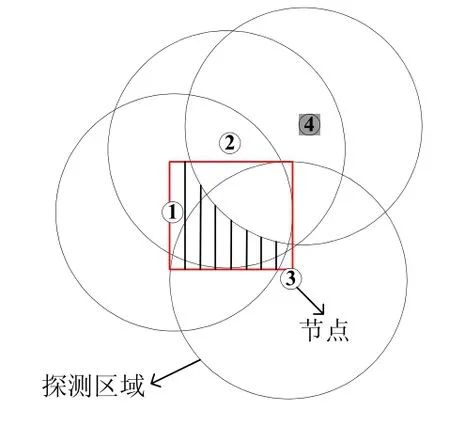
图2 定位算法原理示意图
基于m-网格的定位算法描述如下。
1)先通过邻居节点表中探测到目标的节点的位置信息,得到目标位置可能存在的矩形区域。假设邻居节点表中有假设有N个节点探测到目标,第i个节点的坐标为(xi,yi),节点的探测半径为R,通过
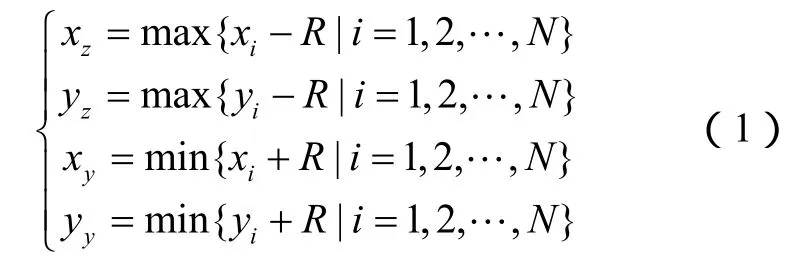
可计算出目标存在的矩形区域的左下角坐标(xz,yz)和右上角坐标(xy,yy)。
2)将矩形区域划分成m个网格,得到每个网格中心点(网格点)的位置坐标。网格的划分方法是将矩形区域在横坐标方向上平均分成n等分(打n-1条纵线),在纵坐标方向上平均分成n等分(打n-1条横线),这样就得到了n×n个网格。由
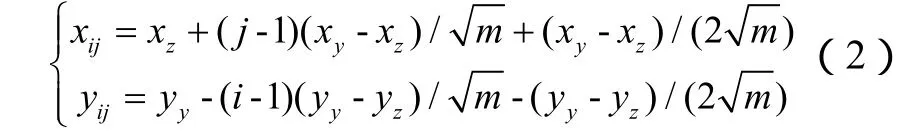
可以计算出目标可能存在区域中第i行、第j列的网格对应的网格点坐标(xij,yij)。
3)计算每个网格点与邻居节点表内没有探测到目标的节点的距离,若该距离小于探测半径,则删掉该网格点。
4)若剩余的网格点集合为空,取矩形区域的中心位置作为对目标位置的估计;否则,取剩余网格点位置的平均值作为对目标位置的估计。
通过以上描述,可以看出基于m-网格的定位算法的计算复杂度与m的大小以及节点邻居中未探测到目标的节点的个数(设为l)相关。该算法的主要运算是求定位点与未探测到目标的邻居节点的距离,根据算法的描述,该算法最多要做lm×次距离计算。在实际运用中,可以通过控制m的大小来调节计算复杂度,节约节点处理器运算时耗费的能量。
4 仿真分析
为验证本文算法的有效性,进行了仿真分析,并与质心定位方法进行了比较。假设监测区域为 100 m×100 m的方形区域,坐标原点设在传感器网络覆盖区域的左下角;100个二进制临近传感器节点以均匀分布的方式随机散布在该区域,节点探测半径为 10 m,节点采样周期为1 s;目标从传感器网络覆盖区域的左下角向右上角匀速运动,即目标的初始位置为(0 m,0 m),速度为(1 m/s,1 m/s)。在仿真中,记录每个定位时刻的定位距离误差,然后取该次仿真中各个定位时刻定位距离误差的均值,作为不同定位方法定位精度的比较标准。
图3为节点通信半径取2倍节点探测半径,m取不同值时,本文定位方法的平均定位误差杆图。从该图可以看出,并不是m值越大,定位精度就越高,当m值增加到一定大小时,定位精度反而会下降。在该图中,当m=64时,平均定位距离误差最小为3.05 m,当m=4时,平均定位距离误差最大为3.81 m。对于质心法而言,平均定位距离误差为4.05 m,这说明本文定位算法精度高于质心算法。
图4为m=36时,不同通信半径下(节点探测半径的1倍~3倍),本文算法和质心定位算法的平均定位距离误差的比较。从图中可以看出,通过增加节点通信半径的方式提高定位算法的平均定位距离误差有一定的极限,对于质心定位方法,当节点通信半径提高到2倍节点探测半径时,极限达到;而对于本文方法,当节点通信半径提高到 2.6倍节点探测半径时,极限达到。同时,在不同的通信半径下,本文算法的定位精度要高于质心算法。

图3 m的取值对本文算法定位精度的影响
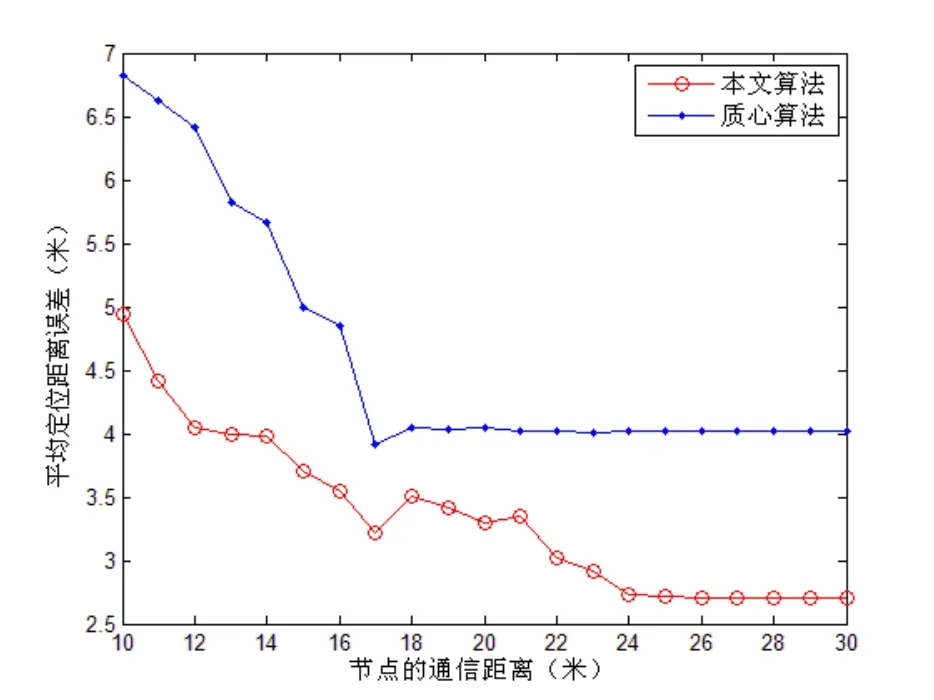
图4 节点通信距离对定位算法估计精度的影响
图5给出了不同m取值下,不同通信半径对本文定位算法精度的影响。从图中可以看出,不同m取值下,通过增加节点通信半径来提高算法的定位精度均存在一定的极限,对于本态势而言,节点通信半径大于26 m时,平均定位距离误差将不再降低;而且,对本态势而言,m取81,节点通信半径取26 m,平均定位距离误差将降到最低为2.35 m,较质心定位法定位精度提高 42%(质心定位法的平均定位距离误差为 4.02 m);从降低算法计算复杂度的角度看,也存在着次优选择,如m取25,节点通信半径取26 m,此时平均定位距离误差为2.40 m,较质心定位法定位精度提高40%(质心定位法的平均定位距离误差为4.02 m)。

图5 节点通信距离对不同m值的本文算法的影响
上述仿真表明,在本文所给协作方式下,本文算法的定位精度高于质心定位法,而且适当调整节点的通信半径(在已知节点探测半径的情况下)和m的取值,本文算法能够提供较质心定位法更高的精度。
5 结束语
分布式二进制传感器网络中的目标协作定位问题涉及到节点的协作和目标定位算法两个重要方面,本文从简单协作的角度出发,提出的简单的协作方法使得每个节点通过简单的广播通信,就可以知道自己邻居节点探测目标的情况,通信量很小。对于单个节点而言,仅当目标进入或离开其探测区域时,才对目标进行定位。所提出的基于m-网格的定位方法,原理简单、易于实现、计算复杂度可调节,可以提供比质心法更高的定位精度。本文考虑的节点探测模型比较理想,在应用本文方法时,需要将实际传感器探测模型进行分析,从软件上改进其判决目标是否存在的方式,使其与理想的探测模型较为一致。如对于测量声音能量的传感器,可以满足较小恒虚警需求的硬判决阈值,然后设置节点声音能量多次超过阈值才判断发现目标(这对于节点探测半径较大,探测的目标速度很慢的应用场合是可以的),这样虚警概率将降到很低。在下一步研究中,我们将重点考虑节点探测的不确定性对本文算法的影响,对算法进一步改进,提高其鲁棒性。
[1]Chong C Y,Kumar S P.Sensor Networks: Evolution,Opportunities,and Challenges[C].Proceedings of the IEEE,USA,August 2003: 1247-1256.
[2]Kim W,Mechitov K,Choi J Y,et al.On Target Tracking with Binary Proximity Sensors[C].Proceedings of the 4th International Conference on Information Processing in Sensor Networks,Piscataway,NJ,USA,2005: 301-308.
[3]Mechitov K,Sundresh S,Kwon Y,et al.Cooperative Tracking with Binary-Detection Sensor Networks[R].Technical Report UIUCDCS-R-2003-2379,University of Illinois at Urbana-Champaign,September 2003.
[4]邓克波,刘中.基于无线传感器网络动态簇的目标跟踪[J].兵工学报,2008,29(10):1197-1202.
[5]申兴发,李鸿斌,赵军,等.面向目标跟踪的传感器网络分布式组管理机制[J].仪器仪表学报,2007,28(6):966-972.
[6]Zijian W,Eyuphan B,Boleslaw K.S.A Distributed Cooperative Target Tracking with Binary Sensor Networks[C].IEEE International Conference on Communication Workshops,May 2008: 306-310.
[7]Djuric P M,Vemula M,Bugallo M F.SIGNAL PROCESSING BY PARTICLE FILTERING FOR BINARY SENSOR NETWORKS[C].2004 IEEE 11th Digital Signal Processing Workshop & IEEE Signal Processing Education Workshop,Taos,NM,USA,August 2004: 263-267.
[8]Djuric P M,Vemula M,Bugallo M F.Target Tracking by Particle Filtering in Binary Sensor Networks[J].IEEE Transactions on Signal Processing,2008,56(6):2229-2238.

