六轮机器人小车的转向特性研究＊

金 龙 李文锋 李 斌

（武汉理工大学物流工程学院 武汉 430063）

在汽车运动分析领域，对车辆的前轮转向、四轮转向已经进行了较为深入的分析［1］.汽车的底盘结构均为矩形，并且多为四轮结构，对于特殊底盘结构的智能车辆并不适用，也缺乏对六轮汽车转向性能的分析.国内外有许多关于六轮智能车辆转向特性的研究［2－3］，其底盘结构都类似于汽车底盘结构［4－5］.研究方法大都基于汽车领域的前轮转向和四轮转向结构.其中包括差速驱动、两轮转向、四轮转向以及全转向.差速驱动的转向主要依靠在地面滑移实现，具有不确定性.两轮转向和四轮转向的实质是假设其转向圆心位于另外不转动车轮的轴线上，其结构类似于汽车领域的四轮转向结构，并且有失一般性.全转向结构是将其中的两个车轮作为万向轮处理，其实质也属于汽车领域的四轮转向范畴.对于特殊底盘结构的六轮智能车辆并未有深入的转向特性的研究.本文以一种新型的六轮小车的底盘结构为研究对象，深入研究了六轮小车转向系统的转向性能.建立了小车转向的运动学模型，并进行合理的简化，对其动态特性进行了分析.通过改变参数，进行仿真，分析了小车行驶速度对转向性能的影响.

1 假设条件

为了使研究方便，现对机器人小车作如下理论性假设［6－7］：（1）假设车辆行驶于平坦路面，建立小车局部坐标系XOY，O为小车的质心，X轴为小车纵向，Y为小车横向，Z轴垂直于地面.小车沿X方向的行驶速度不变，忽略与行驶动力学相关的垂直力影响及耦合作用；（2）认为车体结构是刚性的，各部件不存在弹性变形，忽略转向系统中的不确定因素；（3）车辆的行驶速度较慢，车速恒定，不存在惯性力，也没有空气阻力作用，车体转向时不会倾翻；（4）小车始终处于平衡状态，也即车轮转角足够小，从而保证车辆的运动方程为线性；（5）地面与车轮的接触认为是刚体与刚体的接触.车轮与地面之间的最大侧向静摩擦系数充分大，不存在侧向滑动现象；（6）小车的六个车轮认为是同时协调转向，不存在各个车轮之间的相互制约作用.

通过以上假设，本机器人小车被简化为一个具有一个平移自由度（沿Y轴）和一个转动自由度（绕Z轴）的线性二自由度模型.

2 小车转向时的动力学分析

2.1 动力学模型的建立

根据假设可知，小车仅具有沿Y轴方向的平移和绕Z轴方向的转动两个独立的自由度，图1为小车的线性二自由度模型.

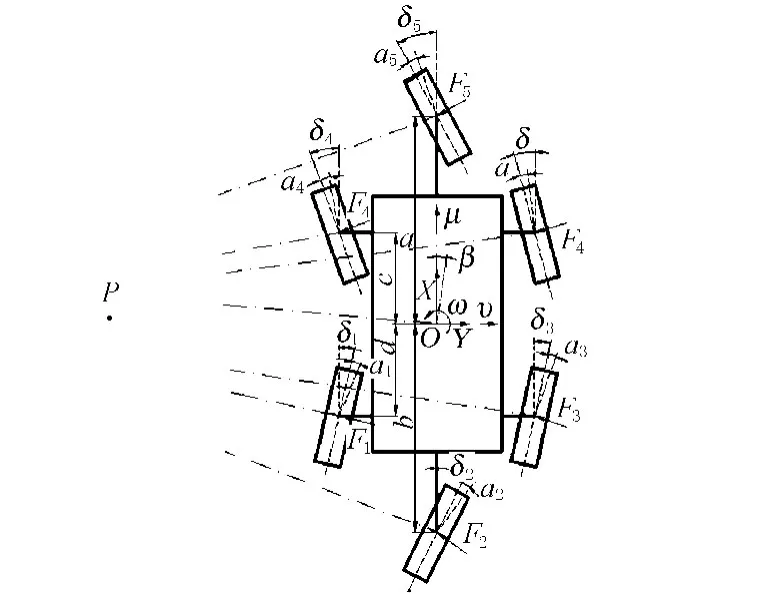
图1 小车的线性二自由度模型

在不考虑小车的势能和耗散能的情况下，用拉格朗日方程建立系统的动力学方程.二自由度六轮小车受到的外力沿车辆坐标系Y轴方向的合力与绕质心的力矩和为

式中：m为小车的质量；Iz为小车绕Z轴的转动惯量.

令各车轮的侧偏刚度为ki，则有，Fi＝kiαi（i＝1～6）.由车体的结构特征有，k2＝k5，k1＝k3＝k4＝k6.

根据坐标系的规定，六个车轮的侧偏角分别为

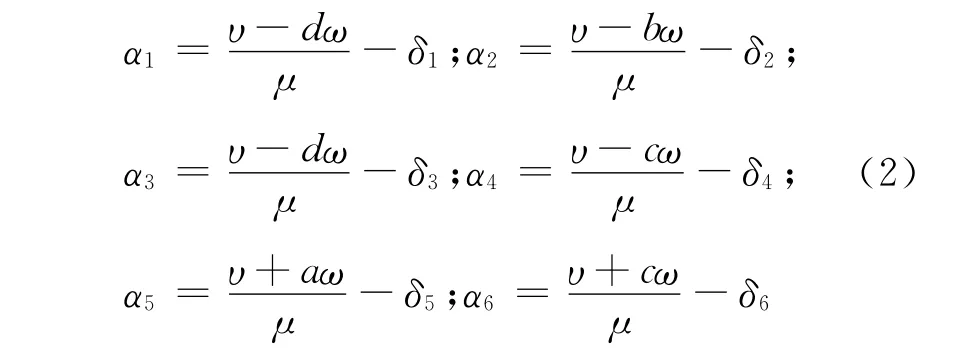
小车质心的侧偏角为

又因为

将式（2）～（4）代入式（1），化简有

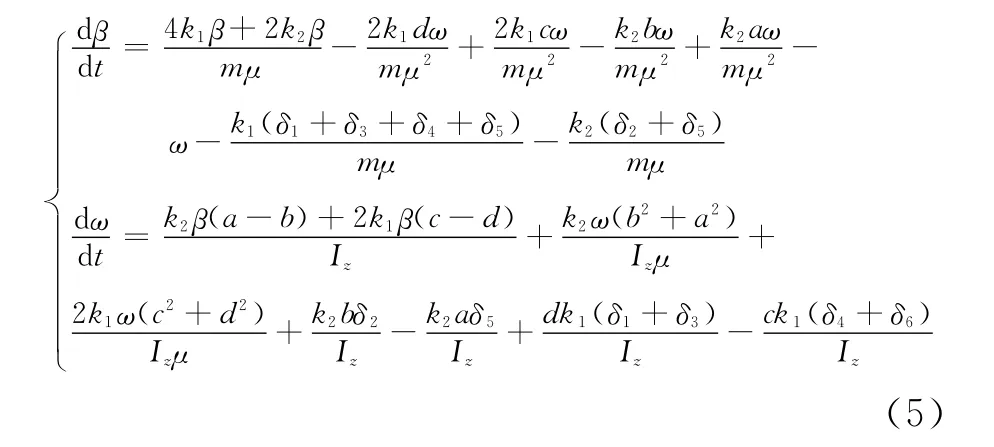
这就是该机器人小车的二自由度运动模型的微分方程.

2.2 模型理论分析

近似取车轮1，3的转角相等，车轮4，6的转角相等，即，δ1＝δ3，δ4＝δ6，并存在如下关系

式中：n1，n2，n3为车轮转角的比例因子.

2.2.1 小车车体横摆角速度与车轮转角的传递函数 将式（5）的两个等式进行变换，得

式中：m1，h1，c1，b1，b0分别为由 m，μ，υ，Iz，k1，k2，n1，n2，n3，a，b，c，d 所确定的表达式.

对式（6）作拉普拉斯变换，可得小车车体的横摆角速度ω与车轮5转角δ5的传递函数

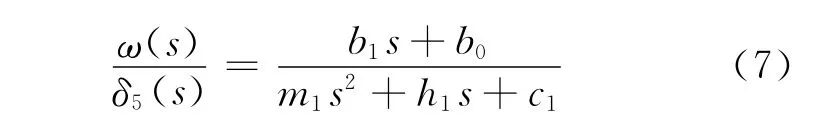
式中：s为复变量.根据式（7），可以求得当车轮转角δ5有输入时，小车车体的横摆角速度ω的变化情况.

2.2.2 小车质心的侧偏角与车轮转角的传递函数 同理，由式（5）的两个等式变换可得

式中：m2，h2，c2，a1，a0分别为由 m，μ，υ，Iz，k1，k2，n1，n2，n3，a，b，c，d 所确定的表达式.

对式（8）作拉普拉斯变换，可得小车质心的侧偏角β与车轮5的转角δ5的传递函数

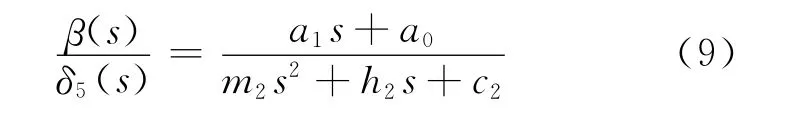
式中：s为复变量.根据式（9），可以求得当车轮转角δ5有输入时，小车质心的侧偏角β的变化情况.

3 仿 真

由2.2中的两个传递函数，用matlab自带的simulink工具箱对其进行仿真［8］.分析各车轮转角成比例的六轮转向小车的时域特性——角阶跃响应特性.把各车轮的转角均转化成车轮5的转角，以车轮5的转角δ5为输入，以小车车体的横摆角速度ω和小车质心的侧偏角β为输出，传递函数如式（7）、（9）.车轮5转角的阶跃信号的起跃时间为0s，幅值为0.1rad，同时以理想阶跃信号施加于其余各车轮，信号起跃时间为0s，幅值为0.1n1，0.1n2和0.1n3rad.

根据线性二自由度机器人小车运动模型的控制策略，化简式（5），得

由车体的结构特点，各车轮转角的比例因子间近似有

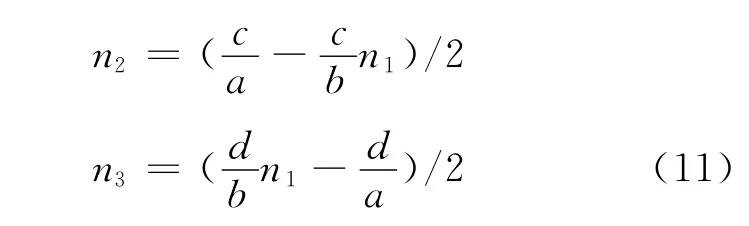
联立式（10）、（11）可以解出n1，n2和n3的值.

分别取车速：μ＝0.05，0.1，0.2m／s，小车的其余参数取为a＝0.8m，b＝0.7m，c＝d＝0.5m，k1＝k2＝45 000N／rad，m＝100kg，Iz＝150kg·m2.

不同车速下小车车体的横摆角速度ω随时间t变化的仿真结果如图2所示.小车质心的侧偏角β随时间t变化的仿真结果如图3所示.

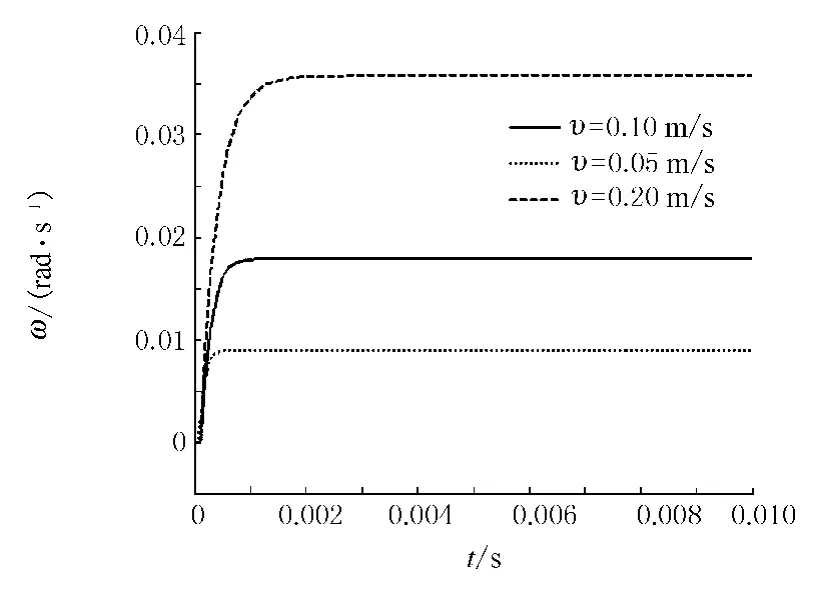
图2 不同车速下小车车体的横摆角速度ω随时间t变化的仿真曲线

图3 不同车速下小车质心的侧偏角β随时间t变化的仿真曲线

仿真的开始时刻，在三种速度的情况下，小车车体的横摆角速度ω都迅速增大，然后趋于稳定.图2中的实线、点线和虚线分别代表υ＝0.1，0.05，0.2m／s时的仿真曲线.图中υ＝0.2m／s时横摆角速度ω的稳定值最大，为0.035rad／s.υ＝0.05m／s时最小，为0.009rad／s.因此，小车车体的横摆角速度ω随着小车纵向速度υ的增大而增大.

当小车纵向速度为υ＝0.2m／s时，小车质心的侧偏角β的均值最大，为－0.2×10－3rad.υ＝0.05m／s时，β的均值最小，为－0.9×10－3rad，如图3所示.图3中三条曲线所代表的车速与图2相同.车速越大，质心侧偏角β的均值也就越大.同时，当υ＝0.2m／s时β的震荡幅度为0.4×10－3rad，υ＝0.05m／s时为1.7×10－3rad.由此可以看出，小车纵向速度u越小，其质心的侧偏角β的震荡幅度就越大，说明小车转向时的运动方向震荡变化的越剧烈，因此小车转向时的稳定性越差.

4 结 束 语

本文以一种特殊结构的六轮机器人小车为研究对象，通过假设条件建立了小车的线性二自由度模型，并由拉格朗日方程得出了该模型的微分方程.利用SIMULINK工具箱对该模型进行时域性仿真，得出了该六轮机器人小车的转向特性与行驶速度的关系.增大车速，可以使小车转向时具有更好的稳定性.但是速度的增加，会使小车转向时的灵活性增加，不仅难以控制，甚至由于离心力的作用，还会发生倾翻.因此，小车转向时并不是车速越小越好，而是应该根据车体质量、路面条件等因素选择合理的的行驶速度.

［1］林 程，孟 祥，陈思忠，等.四轮转向车辆转向特性分析及试验研究［J］.北京理工大学学报，2004，24（3）：218－221，264.

［2］王佐伟，吴宏鑫.月球探测车转向系统动力学建模与分析仁［J］.中国空间科学技术，2004（3）：14－20.

［3］Nesnas I A D，Maimone M W，Das H.Rover maneuvering for autonomous vision based dexterous manipulation［C］／／Proceedings of the IEEE International Conference on Robotics and Automation，San Francisco，California，March 2000.

［4］Chang Yong，Tan Dalong，Wang Hongguang，et al.Kinematics analysis of a six－wheeled mobile robot［C］／／Intelligent Robots and Systems，2006IEEE／RSJ International Conference on Oct.2006：4169－4174.

［5］Deng Zongquan，Fang Haitao，Dong Yuhong，et al.Research on wheel－walking motion control of lunar rover with six cylinder－conical wheels［C］／／Mechatronics and Automation，2007.ICMA 2007.International Conference on 5－8Aug.2007：388 －392.

［6］余志生.汽车理论［M］.4版.北京：机械工业出版社，2006.

［7］Crolla D，喻 凡.车辆动力学及其控制［M］.北京：人民交通出版社，2004.

［8］吕红明，陈 南.基于 Matlab／Simu1ink的四轮转向车辆操纵稳定性仿真［J］.系统仿真学报，2004（16）5：957－959.