高尔夫球射程问题的动力学模拟研究＊

高明向 陈定方

（武汉理工大学理学院1） 武汉 430063） （武汉理工大学智能制造与控制研究所2） 武汉 430063）

0 引 言

高尔夫球是一种把享受大自然乐趣、体育锻炼和游戏集于一身的运动，是一种在优美环境中进行的高尚娱乐活动.对高尔夫球类运动规律的研究，将有助于高尔夫球运动的发展.在国外，对高尔夫球运动规律的研究方法除理论和实验研究外，还采用数值模拟方法［1］.在国内则侧重于理论分析［2－3］，而在实验研究和数值模拟上做得还不够.在这些文献中，为了分析和表示的方便，多将一些对球的运动影响较小的因素忽略不计，并把空气的阻力系数当成常量处理，因而得到的理论分析结果和实际情况有一定差别.

尽可能多地考虑影响高尔夫球运动的因素，建立高尔夫球运动微分方程，利用数值模拟方法，对高尔夫球的运动进行动力学模拟，可以最大限度地获得其真实的动力学行为，无论对于工程应用还是游戏娱乐都具有很大的实际意义.本文针对球员能够控制且对射程有明显影响的因素进行了动力学模拟与分析.

1 高尔夫球的运动微分方程

设高尔夫球的质量为m；半径为r；质心速度为u，是位置x和时间t的函数；为单位速度矢量，绕过质心的轴转动的角速度为ω；g为重力加速度；ρ为空气密度；Cd为空气的阻力系数；μ为空气的动态粘滞系数；A为球的特征面积；V为球的体积；Fw为风对球的作用力，也是位置和时间的函数，可以根据实际需要建立不同的风力模型.则球在空气中平动的常微分方程为

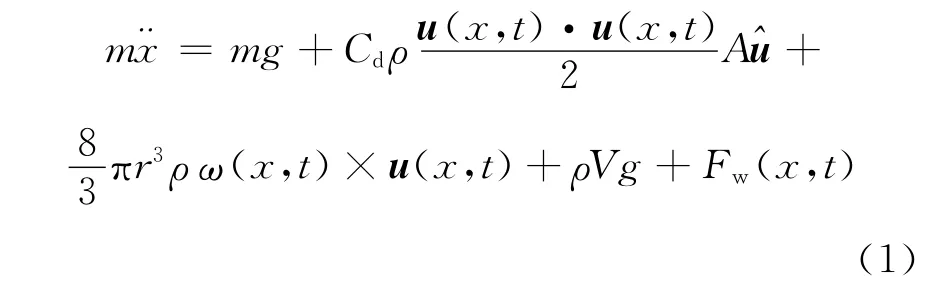
在空气中转动的常微分方程为

方程（1）右侧第1项为球的重力G；第2项为空气阻力Fd；第3项为马格纳斯升力Fl；第4项为空气浮力Ff；方程（2）右侧为空气对球的阻力矩τ.

下面根据此2方程对高尔夫球的射程问题进行数值模拟，并对结果进行分析.下文提到的粗糙球是指现代高尔夫球（网纹高尔夫球）.

2 阻力与光滑程度和球速的关系

当高尔夫球在空气中飞行时，由于其速度比较高，空气阻力所产生的影响就显得十分明显.对于大小相同、初始速率相等的球来说，其所受空气阻力的差异表现在Cd的不同，Cd则与球表面粗糙程度以及雷诺数Re有关.

图1反映了Re＞4×104时，粗糙球与光滑球的Cd与Re间的关系.当Re＜4×104时，由于光滑球与粗糙球表面形成的边界层都是层流，边界层的分离点大致相同，压差阻力也差不多一样.但是，由于粗糙的表面会增加摩擦阻力，因而此时粗糙球也会比光滑球受到更大的阻力.

图1 粗糙球与光滑球的Cd与Re间的关系

如图1所示，对于光滑球，当Re超过3×105时Cd突然减小，对于粗糙球，当Re超过0.5×105时开始减少，而接近0.75×105时Cd达到最小.优秀高尔夫球运动员的击球速度可达到61 m／s，可以计算，对于实际的高尔夫球，在1标准大气压下，20℃时，此速度下，Re＝1.73×105，根据图1，在此雷诺数下空气对粗糙球的阻力系数约为0.26，而对光滑球的阻力系数约为0.48（图中已用虚线标出）.因此粗糙球受到的空气阻力要比光滑球小得多.但速度为31m／s时，Re＝0.75×105，根据图1，空气对二者的阻力系数相差更多.

随着雷诺数的增加，当超过4×105时，从图1中看到，空气对粗糙球的阻力系数反而超过了光滑球.此时的球速大约为140m／s，一般情况下，很难打出这么高的速度.

3 高尔夫球射程的动力学模拟［4－5］

3.1 射程与初速率及表面光滑程度的关系

针对光滑球与粗糙球进行射程模拟实验，研究初速率对射程的影响，并对光滑球和粗糙球的射程进行比较.结果如下.

环境条件 空气温度为20℃（温度影响空气阻力系数）、无风.

初始条件 球的运行方向为－x轴，并采用理论最佳抛射角［5］，即与地面夹角为45°斜向上抛射，球不旋转.

研究方法 给定初始条件和环境条件，改变初始速率，获取高尔夫球飞行过程中的数据，使用Microsoft Excel软件处理数据.

图2反映了粗糙球的射程与初始速率的关系.从图中可以看到，在一定的初始速率范围内，增加球的初始速率能够有效地增加射程.大约在23～50m／s的范围内，球的射程几乎随着初始速率的增加而线性地增大，当初始速率超过50m／s时，随着初始速率的增加，射程的增量开始减小.

图2 射程与初始速率的关系

通过对粗糙球与光滑球的射程差（粗糙球射程－光滑球射程）及射程比（粗糙球射程／光滑球射程）与初速率间的关系进行模拟，结果显示，二者之间的最大比值约为1.66，即粗糙球的射程是光滑球的1.66倍，此时球的初始速率在70～100 m／s的范围内，一般情况下，球的初始速率都要低于此值，此时的射程比为1.2～1.6之间.

模拟结果还表明，当初始速率低于23m／s时，光滑球与粗糙球的射程无差别，高于80m／s时射程的增大量变得越来越小，超过115m／s时，粗糙球的优势就变得越来越小了，这种优势随着初始速率的增加几乎线性地减小，当速度超过160m／s时，光滑球反而比粗糙球飞行得更远.这是由于，如图1所示，此时空气对光滑球的阻力系数要小于对粗糙球的阻力系数.所以，现代高尔夫球的极限初始速率应该控制在160m／s以内.

3.2 抛射角对射程的影响

通过抛射角对射程影响的模拟，得到了最佳抛射角与初始速率的关系，模拟结果如下.

环境条件 空气温度为20℃（温度影响空气阻力系数）、无风.

初始条件 球的运行方向为－x轴，球不旋转.

研究方法 给定初始条件和环境条件，改变抛射角，获取高尔夫球飞行过程中的数据.

模拟结果显示，不同的初始速率下，最佳抛射角并不相同.初始速率为10m／s时，最佳抛射角约为44°，此时的射程约为9.67m；初始速率为31.09m／s时，最佳抛射角约为35°，此时的射程约为74.63m；初始速率为61m／s时，最佳抛射角约为42°，此时的射程约为196.31m；而当初始速率增至75m／s时，最佳抛射角约为41°，此时的射程为235.52m.模拟试验表明，当考虑到旋转的影响时，射程会超过这个数值，但最大射程不会超过300m，这就是现代小型高尔夫球场要求洞间距在300m以内，而球的飞行速率设计为最高75m／s的原因所在.

图3反映了最佳抛射角与初始速率间的关系.初始速率低于20m／s时的最佳抛射角均为44°，随着初始速率的增加，最佳抛射角在减小.当球速接近31m／s时，最佳抛射角将减小为33°，高于此速率时，最佳抛射角又开始增大，但不超过43°，而当初始速率高于55m／s时，抛射角又开始减小，并渐渐趋向35°的抛射角.初始速率高于160m／s时，就要更换为光滑的球了，因而不需考虑此时的抛射角问题.

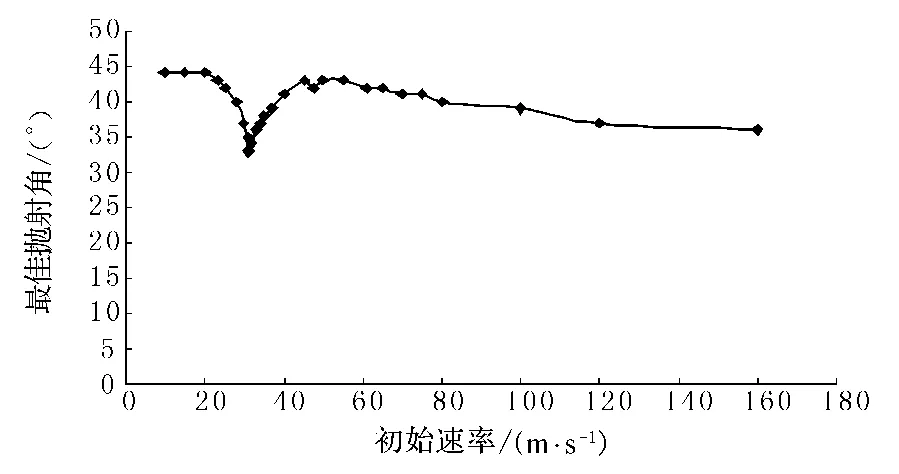
图3 初始速率与最佳抛射角的关系

3.3 转速对射程的影响

旋转对高尔夫球的射程也有明显的影响.从球手的角度看，球的旋转可以分为上旋、下旋、侧旋等，其中，上旋将会增大球的射程，而下旋则会减小球的射程，因为下旋时，空气对球的升力将导致球很快下坠.而侧旋则会改变球在空中的路径，从而形成各种各样的飞行姿态，高尔夫球空中飞行的“九形图”［6］就与球的不同旋转形式有关.

旋转对射程的影响，还与球的抛射角有关，不同抛射角下，需要有不同的转速配合才能达到最大射程.下面以61m／s初始速率研究转速、抛射角对射程的影响.

从图4看到，提高转速的同时降低抛射角能够有效增加射程.当抛射角较大时，增大转速对射程的增加并没有太大的好处，相反当转速提高到一定程度后，反而使射程减少，原因在于，旋转所产生的升力不仅在竖直方向上与重力抗衡，还会在水平方向上产生与球运动方向相反的分量，从而加剧了球在水平方向上的减速运动.而当球的旋转速度超过一定数值后，球反而会在空中折回球的抛射点.在其他初始速率下，转速对射程的影响是相似的.

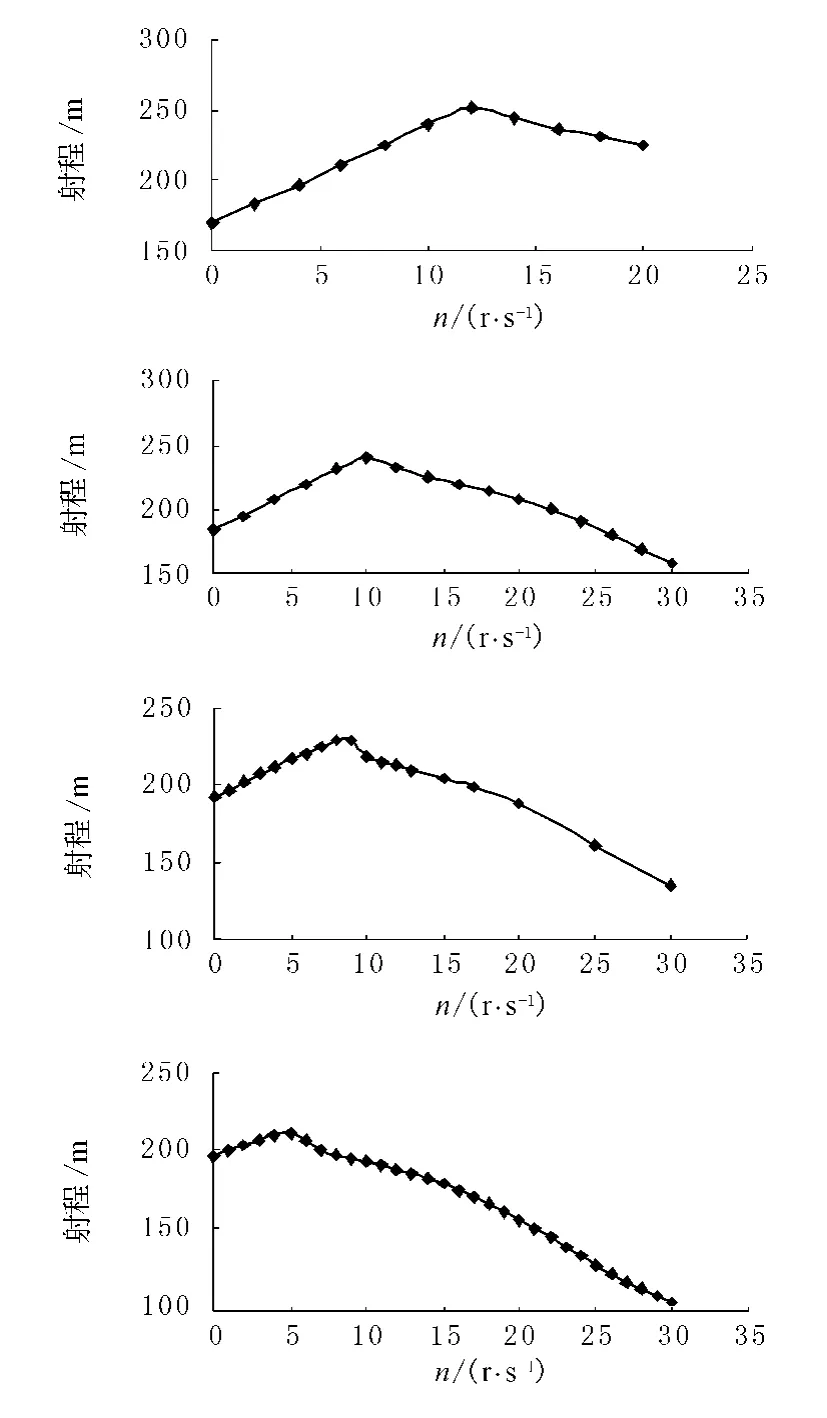
图4 转速、抛射角与射程的关系

4 结 束 语

通过建立高尔夫球的动力学微分方程，并利用空气对不同粗糙程度球的阻力曲线，在初始速率为10～160m／s的范围内对高尔夫球的射程问题进行模拟研究，得出了能够人为控制的多种因素（如初始速率、抛射角度、旋转等）对高尔夫球射程的影响规律，模拟结果与真实高尔夫球的运动非常接近，因而对于增强高尔夫球的击球技术和相关娱乐游戏的开发是有实际指导意义的.

［1］夏皮罗.形与流——漫谈阻力流体动力学［M］.谈镐生，译.北京：科学出版社，1979.

［2］林荣生.流体力学在体育运动中的某些应用［J］.力学与实践，1984（6）：8－14.

［3］刘雅君.高尔夫球射程问题的讨论［J］.大学物理，2005，24（1）：30－32.

［4］高明向.虚拟环境中球形物体的动力学行为建模及其应用研究［D］.武汉：武汉理工大学理学院，2008.

［5］杨宝胜，王淑惠.仰角取何值时铅球抛得最远［J］.物理通报，1990（5）：7－9.

［6］谭受清，熊定勋.高尔夫导论［M］.长沙：国防科技大学出版社，2005.