变压器故障信号去噪方法的研究

黄长铎

（南阳防爆集团股份有限公司物资采购部备件科，河南 南阳 473000）

变压器的运行状态，对电力输送的可靠性具有决定性意义。对变压器进行监测、检修和试验，能使变压器存在的障碍和缺陷得以发现和消除。当变压器发生故障时，由于采集到的信号含有大量噪声信号，这给信号的处理带来了干扰。

传统的基于傅立叶变换进行滤波去噪的前提，是真实信号和噪声信号的频带重叠部分应尽可能的小，即有用信号与噪声分属于不同的频带。只有这样，才能设计出不同频率特性的滤波器，对信号进行滤波，消除噪声的干扰。另一方面，白噪声往往覆盖了各个频段，也包括真实信号的频段，这就给去噪带来了新问题。

利用小波变换检测变压器故障信号的奇异点，是国内外常采用的方法。小波变换是一种新的数字信号处理技术，已被广泛应用于信号处理、图像处理、语音分析、模式识别等众多领域[1～4]。这是由于小波变换具有一种“集中”的能力，可以使得一个信号的能量在小波变换域中，集中于少数的系数上，这些值必然大于能量分散于大量系数上的噪声的小波系数，于是我们就可以选取硬阈值或软阈值的方法，将噪声信号从变换结果中去除。

本文利用小波变换对变压器故障信号进行了去噪处理，仿真结果表明了小波变换在变压器故障信号去噪中的应用价值。

1 小波的概述

小波变换的基本思想，是用一族函数去表示或逼近一信号或函数，这一族函数也就是小波函数系，它是通过一个基本小波函数平移和伸缩构成，用其变换系数即可描述原来的信号[6]。

设小波函数 ψ（t）∈ L2（R）（L2（R）为能量有限空间），其傅立叶变换为，若满足如下的允许条件

时，则称函数ψ（t）为一个基本小波或母小波，其与下式等价：

由于ψ（t）具有一定的振荡性，其包含有某种频率特性。

由基小波ψ（t）通过伸缩和平移，可以生成一族函数族，也就是分析小波，可写为

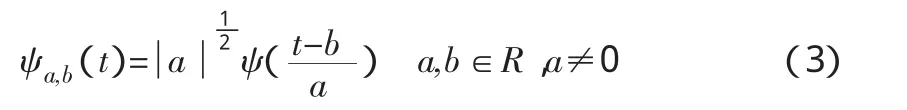
式中，

a称为尺度因子；

b称为平移因子。

小波变换通过ψ（t）在尺度上的伸缩和平移来分析信号，信号 f(t)∈ L2（R）关于分析小波 ψa,b（t）的连续小波变换定义为

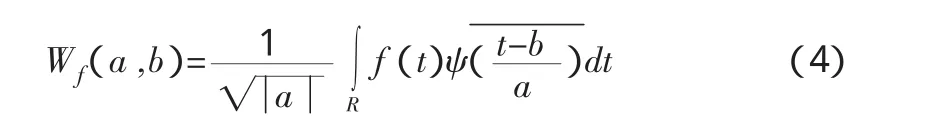
由式(4)可以得知，小波变换 Wf（a,b）是尺度因子a和空间位置b的函数。

由于在实际应用中，需要对连续小波及其变换进行离散，如果只对连续小波的尺度参数进行二进离散（a=,j∈z）而平移参数保持连续变化（b∈R），则小波变换取得半离散的形式

这种小波变换，称为二进小波变换，对应的小波函数ψ（t）称为二进小波，其具有连续小波变换的平移不变性，这是较之离散小波变换的独特性，则有

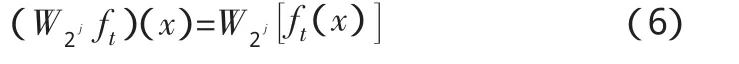
式（6）表明，二进小波变换等于其二进小波变换的平移。

经小波二进分解后，信号f（t）也就表示为不同频率的小波分量，如式（7）表示

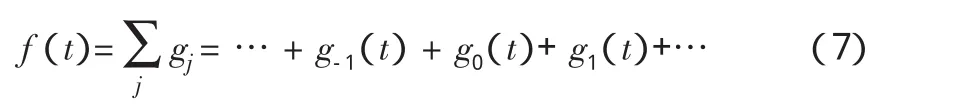
也就是说信号f（t）被分解为二进小波后，对信号的研究就转化为对其小波分量在某一尺度下的小波变换的研究。

在尺度2j下的重构公式为

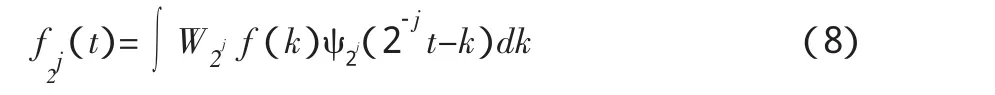
式（8）得到的，就是时间信号是小波变换的重构信号，重构的实质是保持尺度系数一定，仅对平移因子进行积分，得到在特定尺度下的时间信号，其意义在于将信号分解成特定频率范围内的时间信号，对信号进行重构分析，可以排除其他频率成分的干扰。

2 消噪仿真

不同的消噪效果图分别如图1～图3所示。

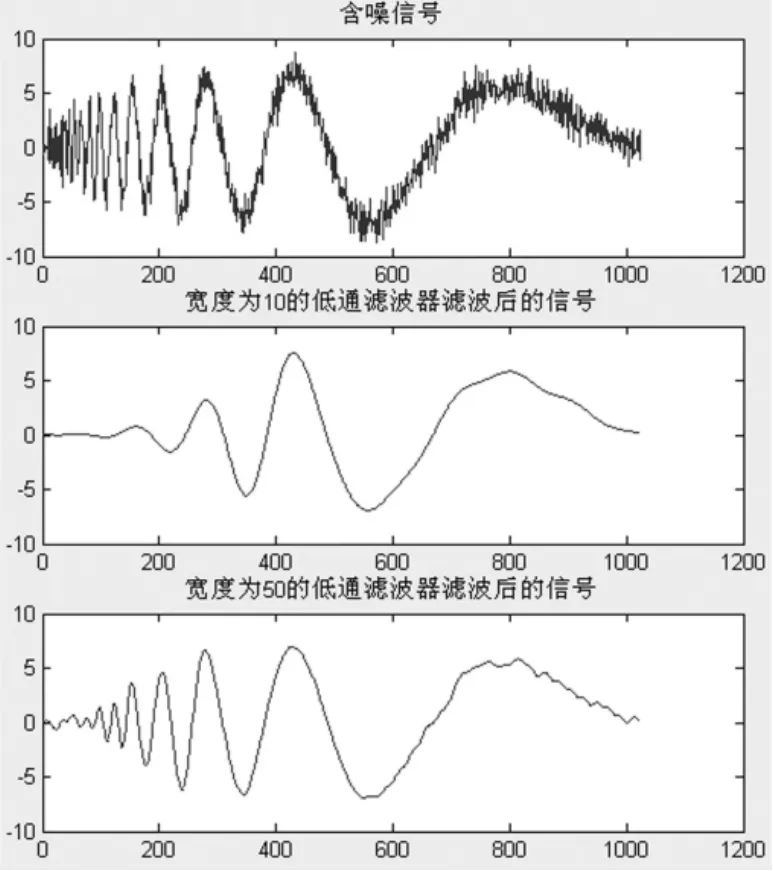
图1 傅立叶变换消噪结果

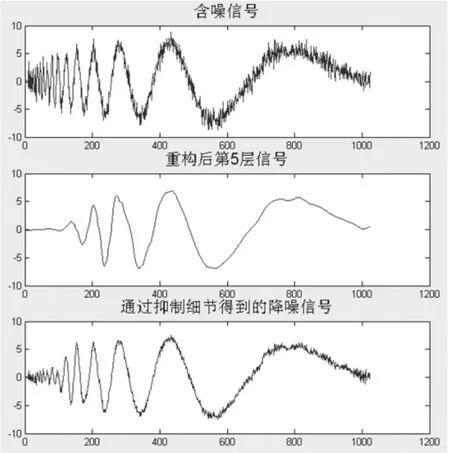
图2 抑制小波系数的消噪结果

图3 阈值消噪结果

从图1可以看出，单纯的傅立叶频域滤波有一刀切的缺陷，也就是把带通之外的频谱不加区分地滤除掉了。

从图2可以看出，使用单纯的抑制细节系数的方式，确实可以实现消除信号噪声的目的，但这种方式太过于粗略，没有通过噪声本身来确定降噪的方法，降噪后的信号损失了很多信号的能量成分，不光抑制了噪声，还抑制了很多有用的成分。

从图3可以看出，小波阈值去噪，很好地保存了信号发展初期的高频特性，且性能优于以往的抑制细节的策略和傅立叶变换，最大限度地反映了信号的本身的特性。

从几个仿真图的对比可以看出，用小波进行信号的消噪可以较好地保存信号中的有用部分，小波消噪效果效果佳。

3 结束语

本文阐述了小波变换用于变压器故障信号去噪的基本理论，并通过仿真验证了将小波用于变压器故障信号去噪的可行性，且去噪效果比傅里叶变换好。

[1]彭 剑.变压器故障在线诊断理论基础与方法[D].长沙：湖南大学，2007.

[2]汲胜昌，刘味果，李彦明，等.小波包分析法在振动法监测变压器铁芯及绕组状态中的应用[J].中国电机工程学报，2001，21(10)：24-27.

[3]高 成.Matlab小波分析与应用[M].北京：国防工业出版社，2007.

[4]胡昌华，杨宗凯.实用小波分析[M].西安：西安电子科技大学出版社，2001.