基于加速度计的起重机吊重摆角测算方法研究

金序南

（同济大学中德学院，上海 200092）

起重机在工作过程中，桥和小车运行时的加速、减速会导致吊重及钢绳绕悬点产生摆振。这种摆振不仅会降低运输及装卸效率，而且会给起重机作业带来不安全因素。智能电子式防摇系统由于将减摇与桥和小车的运行控制将结合起来，具有附加设备少、防摇时间短等优点，成为现今主流的防摇方式。尽管各种智能电子式防摇系统采用的控制策略不尽相同，但是作为系统重要的输入参数之一，精确的吊重摆角检测，对于控制的精度起了十分重要的作用。现今应用的吊重摆角检测系统，按原理可以分为纯数学模型式、机械式以及光学式。纯数学模型方式的难点，是精确的模型很难建立，并且该方法不适合有外部干扰（如刮风）的环境。机械式由于结构和工作条件的原因，限制了应用场合，同时检测元件也容易磨损。光学式主要利用视觉传感器或激光，通过在小车架上安装发射和接收装置，在吊具上安装反射装置来检测。由于光学装置价格昂贵和易受环境影响（如遇浓雾、灰尘等），其使用受到限制。

本研究的主要目的，是改进已经在垃圾处理中心成功应用的起重机系统。由于该起重机使用环境恶劣，并且吊绳长度达36m，以上各种吊重摆角检测方式的使用受到比较大的限制。本文提出在小车和吊具上分别安装加速度计，通过加速度计差值对时间的二次积分，来计算二者的位置差，并利用独立测量的吊绳长度，来测算吊重摆角的方法。该方法不依赖复杂的数学模型，十分简洁明了，易于理解。同时该方法不需要复杂的辅助设备，并且不受一些外部干扰（如强风引起的吊重摆动）的影响，克服了传统吊重摆角检测方法的不足与缺陷，扩大了起重机的使用范围。

1 小车-吊重系统数学模型

由于小车和桥的驱动控制，是基于各自独立的参数检测和控制系统，并且小车和桥在水平面内相互垂直运动，因此可以将两者的运动看作是非耦合运动。因为小车和桥的运动情况类似，所以本文仅研究小车在水平移动的同时提升载荷的情况，以此将空间摆运动简化为平面摆运动。

小车-吊重系统的简化力学模型分析如图1所示。其中，mK和mL分别表示小车和吊重质量，F为小车牵引力，FM为小车运行阻力，x表示小车水平方向位移，l为吊绳长度，φ表示吊重摆角，g为重力加速度。为方便描述分析，在该系统中分别设置小车坐标系（K系）和吊重坐标系（L系）。其中，小车坐标系的原点为小车质心，横坐标平行于运动导轨，向右为正方向；纵坐标竖直过吊绳悬挂点，向上为正方向。吊重坐标系的原点为吊重质心，纵坐标与吊绳重叠，向上为正方向；横坐标垂直于吊绳，向右为正方向。

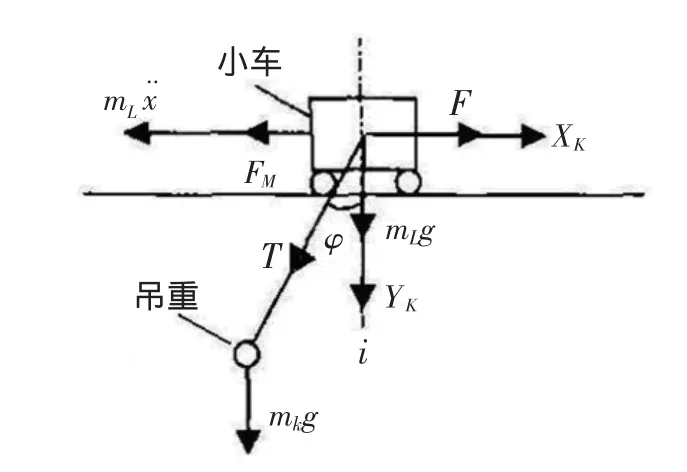
图1 小车-吊重系统

小车-吊重系统运动的微分方程可由达朗伯-拉格朗日原理导出。对于由质量mi，矢径为ri的质点Pi（i=1,2……n）所组成的、受主动力Fi作用的质点系，达朗伯-拉格朗日方程可表示为

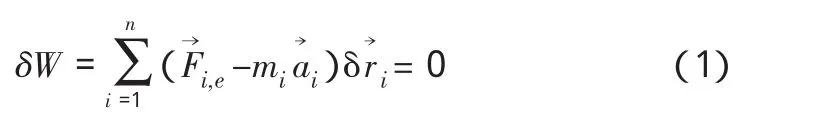
即对具有理想、双面约束的非自由质点系，在任一瞬时，作用于该质点系的主动力及惯性力在系任意虚位移上所作的功之和等于零。

小车-吊重系统中，各质点的位置在广义坐标系中可以通过3个独立坐标确定，即小车水平方向位移x、吊重摆角φ以及吊绳长度l。同时规定，当吊重位于小车垂线左边时，吊绳摆角为正。小车和吊重位置可分别如下表示：

由式（3）可得吊重虚位移

小车-吊重系统达朗伯-拉格朗日方程为

将各式分别代入式（10）后可得

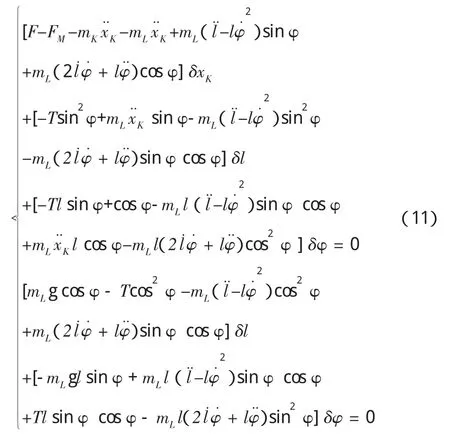
若要使式（11）中的两个等式在任意 δxK、δφ 和 δl下都成立，必须令各个中括号内的值为零，即

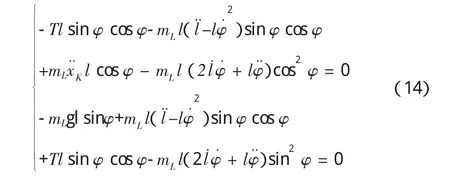
化简整理后得小车-吊重系统数学模型

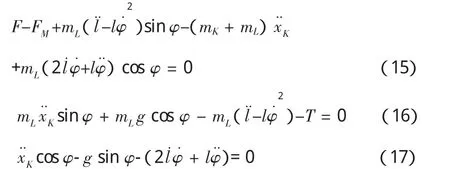
式（15）为小车在小车坐标系X轴（XK）上运动微分方程。式（16）为吊重在吊重坐标系Y轴（YL）上的运动微分方程。式（17）为吊重在吊重坐标系X轴（XL）上的运动微分方程。吊重的受力如图2所示。

图2 吊重受力平衡

2 仿真参数与仿真结果

在现代吊车中，通过控制吊重提升电机，可以得到相对恒定的输出转数，因此吊重的提升速度可以认为是恒定的。同时，通过控制小车驱动电机的转数，可以把小车的加速度、减速度近似地看作恒定值。由式（17）可知，无关吊重质量如何变化，只要确定了小车运行加速度的大小与方向，就能确定吊重的摆角，吊重的加速度也就相应得到确定。

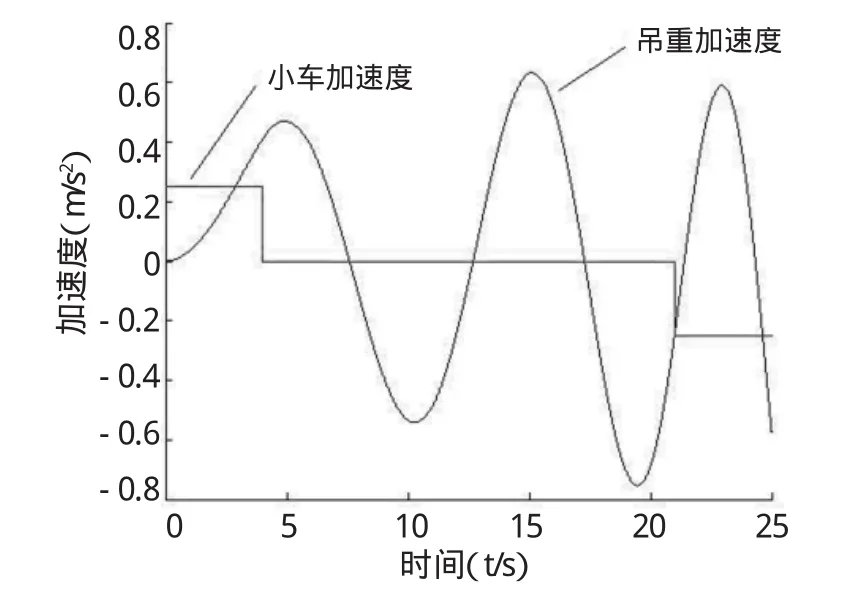
图3 小车和吊重加速度

模拟起重机运行过程如下：小车先从静止开始匀加速一段时间，再作匀速运动，最后匀减速直至停住。在小车运行的同时，吊重沿绳子方向匀速向上提升。

本研究作为在垃圾处理中心成功应用的起重机系统的改进，为真实地模拟运行情况，仿真参数大部分参考实际应用参数。具体参数如下：小车总质量11386 kg，吊具总质量8000 kg，小车最大允许负载质量（吊具质量加吊重质量）16000 kg，小车加速度0.25m/s2，小车加速时长4 s，小车减速度-0.25 m/s2，小车减速时长4 s，小车匀速运行时长17 s，小车匀速运行速度1m/s，重物提升速度1m/s，初始绳长36m，初始摆角为0°。仿真结果如图3所示。

3 加速度计的选择

本研究计划直接采购整套加速度测量设备，包括加速度传感器、专用连接线、放大器、数据采集器以及配套软件。

加速度计的选用，应该考虑以下3个方面：

（1）工作频率范围。由仿真结果可知，被测量的吊重加速度是动态变化的，其频率范围约为0.1～0.3Hz。因此所选择的传感器的工作频率范围应该覆盖被测频率。

（2）分辨率。由仿真结果可知，吊重加速度的幅值约为0.7m/s2，故所选取的加速度传感器的分辨率必须小于该幅值。

（3）现场环境。由于实际工作的现场环境比较复杂，必须选择工作温度适合的传感器。

综合考虑以上各项性能指标，并结合工业应用要求，我们最后选择使用德国HBM公司生产的B12/200加速度传感器，及其配套设备进行实验。该传感器为基于弹簧-质量系统的电感式加速度传感器，既可以测量恒定加速度，也可以测量振动和冲击加速度。B12/200传感器的工作频率范围为0～100 Hz，分辨率可达0.02m/s2，测量范围为±200m/s2，净质量只有17 g，具有灵敏度高、温度漂移低、体积小、净质量小的优点。在传感器校准时，只需要在其两端分别位于竖直向下位置的同时，在放大器中输入0 g和2 g的数值即可。该校准方法十分简便，非常适合于工程应用。

4 实验平台组成结构

为了更贴近起重机真实的运行情况，我们特地将实验安排在德国德马格（DEMAG）起重机公司的实验场地。实验平台完全利用该公司所售的产品搭建，可以通过人工操纵小车运行，其组成部分为：小车、轨道、控制手柄、吊具、吊重，如图4所示。

图4 实验平台

在实验平台中，小车的技术参数与真实应用的不同，吊绳长度为3.5m。由于本实验主要研究在小车运行时吊重加速度的变化，而且小车由于沿着导轨运行，其运动情况，包括加速度、速度和位移，可以分别由不同的传感器测得，出于简化实验的目的，通过固定在小车上的测速电机和周长为0.5m的测速轮，来测量小车的运行速度。安装加速度传感器的支架，被用胶布粘在质量为6.3 t的吊重顶部中间位置，其壳体轴向与小车运行方向重合，并通过配套连接线将其与专业测量放大器连接。加速度传感器的信号和测速电机的信号，通过信号采集器以1000次/s的频率采集并被保存。

5 实验结果与分析

由于实验条件的限制，实验平台无法真实地模拟起重机在垃圾处理中心的运行情况。因此，在下面的分析中，我们将通过利用测速电机所测得的小车的速度，来计算其真实加速度，并利用所计算的小车真实加速度和吊重摆动的数学模型，来求得吊重的理论加速度，并将其与传感器测得的实际加速度进行比较。

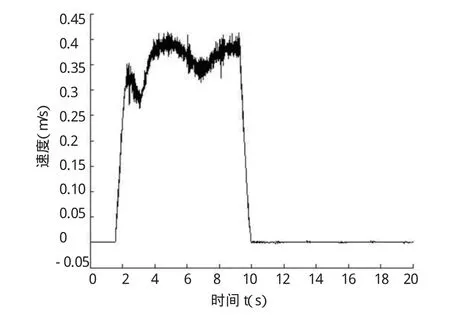
图5 测速电机测量值

图6 加速度传感器测量值

图5和图6分别为测速电机和加速度传感器的输出。通过滤波后发现，加速度传感器的测量值远远小于理论值，但其变化趋势与理论值一致，因此将传感器的输出进行放大。

放大因子通过如下方法确定：小车停止后，测量吊重摆角的幅值约为2.5°，利用吊重摆动数学模型来模拟吊重，以该幅值摆动时的理论加速度幅值，通过该幅值与传感器测量的加速度幅值进行比较，确定放大因子为8.3。图7所示为吊重修正后加速度、吊重理论加速度以及小车实际加速度。图8所示为到小车停止时，利用吊重修正后加速度和理论加速度分别计算的吊重摆角。

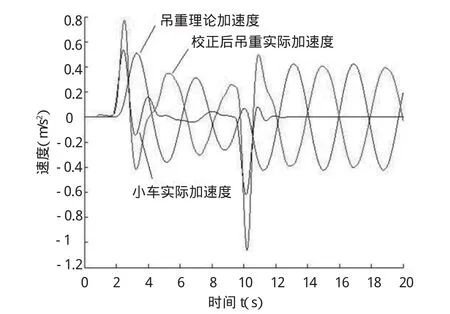
图7 吊重修正后加速度、吊重理论加速度以及小车实际加速度

图8 吊重测算摆角和理论摆角

从图8可以看出，摆角测算值和理论值相差比较大，其具体原因分析如下：

（1）吊车理想模型与实际运行情况的差别。在数学模型中没有考虑吊重摆动对小车的影响，但从图5上可以看出，小车在运行过程中，因轮子滑动而造成速度的波动。另外，从图7上可以看出，虽然在大多数情况下，吊重理论加速度和实际加速度的幅值基本相同，但由于在小车加速、减速阶段，吊重实际摆动速度要快于通过数学模型得出的理论值，因此造成真实曲线和理论曲线的相位差。为消除该影响，可以通过其他方法测量吊重的真实摆角，并以此作为理论值来跟测算值进行比较。

（2）低频测量时传感器的测量偏差。测偏差主要由传感器的工作原理所造成，虽然在实验数据中应用了一些纠偏方法，但不够精确。

（3）实验过程中的干扰。从图6和图7可以看出，传感器由于测量时受到高频信号的干扰而产生锯齿状曲线。为了消除高频干扰，必须首先对测量结果进行滤波。但是不同的低通滤波器设计会使滤波结果有比较大的差异，从而影响实验结果的精度。

（4）吊重转动的影响。吊重在摆动的同时，也可能会以吊绳为轴转动，使传感器测量轴方向跟吊重实际摆动方向不重合，从而导致测量结果不准确。为了消除该影响，可以对吊重的转动角度另外进行测量，并以此对传感器测量值进行修正。

（5）传感器校准、安装等影响。实验前虽然对传感器进行了简单的校准，但为了提高测量精度，最好通过专门仪器来校准。另外，如果传感器安装表面有斜度，或者安装时，传感器的测量轴没有跟吊重实际摆动方向重合，这些情况都会影响测量精度。

（6）累积误差。吊重的位置通过加速度两次积分求得，由积分的特性可知，所有的测量误差将会累加，从而使计算误差随时间的增加而增大。从图8上可以看出，测算的摆角值在实验后半段比前半段大。为了限制累积误差，可在实验过程中对计算结果进行修正，比如过一定时间后，当检测到实际摆角为零时，修正摆角的计算结果。

6 结束语

通过建立吊车载荷摆动的数学模型，利用小车运行的加、减速度来仿真吊重摆动，得到吊重的理论加速度值，并利用该结果选择合适的加速度传感器进行实际测量。同时对比吊重加速度实际测量值与理论值，分析了吊重实际摆动与理论模型的区别，提出一种在低频测量时对传感器的测量结果进行修正的方法，并利用修正后的数值计算出吊重摆角。由于理论模型与吊车实际运行情况存在比较大的差别，并且传感器在低频测量时误差较大，实验虽然取得了一定的成果，但还需要针对已发现的问题作进一步改进，同时研究开发适合传感器低频测量的测量电路和纠偏算法，进行精确测量。

[1]薛定宇，陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京：清华大学出版社，2002.

[2]肖 鹏.一种新型的桥式起重机位置补偿消摆控制策略[J].机电工程，2005，11(39):1250-1253.

[3]王帮峰，张瑞芳，张国忠.回转起重机吊重振摆的动力学模型与控制[J].中国机械工程，2001，12(11):1214-1217.

[4]吴 晓，钟 斌.小车吊重系统摆阵动力学模型及仿真[J].计算机仿真，2007，（11）:316-319.