无线传感器网络路径覆盖问题研究

李 磊 张宝贤 黄河清 刘海涛

①(中国科学院上海微系统与信息技术研究所 中国科学院无线传感网与通信重点实验室 上海 200050)②(中国科学院研究生院泛在与传感网研究中心 北京 100049)

1 引言

无线传感器网络(Wireless Sensor Network,WSN)是一项新兴技术，被广泛应用于国防、工业、环境、健康等多个领域。在实际应用中，无线传感器网络节点通常是随机分布在目标区域，在某些应用场景下，如环境检测，往往要求区域满足k(k≥1)覆盖，即区域内的每一个点至少被k个传感器覆盖到，这样的问题通常被称为区域覆盖(area coverage)。区域覆盖度能充分反映传感器网络对目标检测区域的覆盖情况，是无线传感器网络QoS指标之一，文献[1-3]对区域覆盖进行了详细的分析。而在另外一些应用场景下，如入侵检测和目标跟踪，人们更加关心的是入侵目标移动路径的覆盖情况，这样的覆盖问题通常被称为路径覆盖(path coverage)。根据实际应用需求的不同，衡量路径覆盖的标准也不同，其中最常用的有以下两种：(1)路径满足k覆盖的平均比例，即目标沿任意路径移动时，该路径满足k覆盖的部分所占的比例。(2)路径满足k覆盖的概率，即目标沿任意路径移动时，该路径上的点全部满足k覆盖的概率。现有的关于路径覆盖的研究往往都是针对直线路径，这是因为在入侵者不知道网络中节点的位置信息时，往往会选择沿直线路径穿越检测区域，这样可以用最少的时间穿越检测区域，从而减小被发现的可能性。本文的研究也是基于这个假设，所以除非特殊声明，后文所提到的路径覆盖都是指直线路径覆盖。针对以上两种覆盖标准，文献[4,5]分别在节点同构(Homogeneous)模型和节点异构(Heterogeneous)模型下对2维区域节点布设密度与路径满足k覆盖的平均比例之间的关系进行了分析，并给出计算表达式。文献[6]对节点布设密度与路径满足1覆盖的概率之间的关系进行了分析，并给出计算表达式，但是并没有给出k(k＞1)覆盖概率的分析。然而，路径k(k＞1)覆盖有着非常广泛的应用场景，比如说当网络用来进行目标跟踪时，为了达到定位的目的，往往要求k≥3[7,8]。另外文献[6]在分析时假设传感器节点的感知半径是相同的，而这一点在实际应用中是很难保证的。因此本文对节点布设密度与路径满足k(k≥1)覆盖概率之间的关系进行了分析，并给出路径满足k(k≥1)覆盖概率的理论下限。实验表明，在k值较小时，本文给出的理论下限与实际仿真结果比较接近。

本文的组织结构如下：第2节给出系统模型和本文所要解决的问题，第3节将2维区域的路径覆盖问题转化为1维线段覆盖问题，第4节给出1维直线段满足k覆盖的概率分析，第5节给出在2维区域内判定直线路径是否满足k覆盖的方法，第6节给出仿真结果，第7节总结全文。

2 系统模型和问题描述

本节首先给出系统模型，然后定义所要解决的问题。本文中“传感器节点”与“节点”含义相同。本文研究的无线传感器网络系统模型基于如下假设：

(1)无线传感器节点按泊松分布随机散布在面积为A的正方形监测区域。令λ表示节点的布设密度，N 表示监测区域的节点数。显然，N服从以λA为期望的泊松分布。

(2)无线传感器节点为同构节点，节点的感知模型采用0/1模型，即：节点以概率1检测以其为中心、以r为半径的圆形检测区域(不包括圆上的点)，这样的感知模型通常被称为泊松布尔模型(Poisson Boolean model)。

(3)本文用xi(0＜i≤N)表示区域内的节点，其感知范围用ri表示，ri的取值范围为(0, R]，概率密度函数用f(ri)表示，期望值用β表示。

本文研究的第1个问题表述如下：

问题1 目标沿某直线路径L移动一段距离s(假设s≫R，且s＜)，求该路径满足k覆盖的概率。

3 问题转化

本节将路径覆盖问题转化为普通的1维线段覆盖问题。由于本文采用的是0/1感知模型，任意节点xi(0＜i≤N)与路径L的距离小于其感知范围ri时，都可以在L上覆盖一定区域，本文用li表示该区域的长度(见图1，不失一般性，假设L位于坐标系的横轴上)，文献[5]给出了li的概率分布函数：

另外，所有与L的距离小于其感知范围ri的节点xi都在L上有一个映射点yi(如图1所示)，文献[5]通过证明给出“yi所形成的点过程是以2λβ为期望值的泊松点过程(Poisson point process)”。这样，图1所示入侵路径问题可以转化为如下1维线覆盖问题：

图1 一条直线路径在2维无线传感器网络中的覆盖情况

问题2 在已知线段L上以密度λ'=2λβ布设节点，节点的感知直径l的概率密度函数为g(l)，求该线段满足k覆盖的概率(见图2)。

图2 问题2给出的1维线覆盖示意图

由于问题2和问题1是等价的，所以问题2的解答显然适用于问题1，另外由于问题2也是一个普通的1维线覆盖问题，因此问题2的解答也适用于其它的1维线k覆盖问题，比如说弱栅栏覆盖(weak barrier coverage)[9,10]。弱栅栏覆盖是指入侵者沿垂直于入侵边界的路线穿越带状检测区域时所引发的覆盖问题，由于该覆盖问题只与节点在水平方向的位置有关，因此同样可以转化为普通的1维线覆盖问题。

为方便后文的表述，定义节点yi的覆盖区域的左边界为起始点(starting point)，yi的覆盖区域的右边界为结束点(ending point)，并用zi表示节点yi的覆盖区域的左边界(见图2)，很显然，这些起始点同样组成以2λβ为期望的泊松点过程。

4 1维线段满足k覆盖的概率建模分析

为了保证1维直线段满足k覆盖，则要求该线段上的任意点都被至少k个节点覆盖，一条线段上有无数个点，因此1维线全覆盖的问题是一个连续域的问题，为了计算1维直线段满足k覆盖的概率，首先需要将该问题从连续域转换到离散域。

本文同文献[4,5]一样假设s≫R，从而忽略掉路径边界效应对结果的影响。为了将该问题转换到离散域以便于计算，首先给出如下定理：

定理1 直线段L满足k覆盖的充分必要条件是该线段上的所有起始点都至少被k个节点覆盖。

证明 必要性是很显然的，如果该线段满足k覆盖，那么这条线上所有的点都满足k覆盖，当然也包括所有的起始点。

然后证明充分性。在1维线段上任取一点u，如果能够证明u为k覆盖，则该线段满足k覆盖。假设v是u右边距离u最近的一个起始点，为了保证点v为k覆盖，则至少有k个覆盖区域的起始点处于v的左边，且其结束点处于v的右方，而u与v之间不存在起始点，所以能够覆盖v的覆盖区域均能覆盖点u，因此点u满足k覆盖。这里，一个“覆盖区域”是指一个节点在目标直线上的覆盖区域。

综合以上两点，该定理得以证明。 证毕

假设2维区域内共有n个节点与路径L的距离小于其感知半径，根据第2节的系统模型，n服从以λ's=2λs β为期望的泊松分布，在s足够大的情况下，n近似取值2λ s β。如果用Ak(i)表示第i个起始点zi(1≤i≤n)被至少k个节点覆盖到这一事件，则根据定理1，L满足k覆盖的概率可以用下式表示：

其中Pr[T]表示事件T发生的概率。在起始点所形成的泊松点过程下，任一起始点满足k覆盖的概率Pr[Ak(i)]可以用下式表示：

其中a=E(l)，式(3)的推导可以参见文献[1]。尽管可以得出某一个点满足k覆盖的概率，但是很显然Ak(i)，1≤i≤n，之间并不一定具有相互独立的性质，因此很难为式(2)求得一个准确的计算形式。本文利用FKG不等式[11]来计算式(2)的下限，FKG不等式是指在泊松布尔模型下，如果有事件B1和B2随着节点密度的增加都是增函数或都是减函数，则有如下性质：

由式(3)可以看出，Ak(i)，1≤i≤n，是节点密度的增函数，则利用FKG不等式有

可以利用式(5)计算长度为s的直线段满足k覆盖的概率下限，特别地，当k=1时，有如下表达式：

5 路径k覆盖的判定方法

在给出仿真结果之前，首先对如何在2维区域判定一条直线路径是否满足k覆盖的方法做一些说明。由于直线路径在2维坐标系中可以是任意走向的，因此，为了简化计算的复杂度，本文首先将其映射到横轴，然后通过判定映射后的线段是否满足k覆盖的方法来判定目标路径能否满足k覆盖。具体流程如下：

首先以正方形布设区域的左下角为原点建立坐标系，假设直线路径的两个端点的坐标分别为(X1,Y1)，(X2,Y2)，不失一般性，假设X1＜X2。为方便描述，本节用[α, ϕ]表示点(α,0)与点(ϕ,0)之间的线段。则线段[X1, X2]就是目标路径在横轴的投影。

然后找出所有与目标路径距离小于其感知半径的节点，假设共有Num个，并计算这些节点在目标路径上的覆盖区域的两个端点的坐标值，分别记这两个端点的横坐标为LPi，RPi，1≤i≤Num。不失一般性，同样假设LPi＜RPi，如果LPi＜ X1，则LPi=X1，如果RPi＞X2，则RPi= X2。则[LPi, RPi]，∀1≤i≤Num，就是节点在目标路径上的覆盖区域在横轴上的投影，显然，如果[LPi, RPi]，∀1≤i≤Num，可以k覆盖线段[X1, X2]，则目标路径满足k覆盖，否则目标路径不满足k覆盖(如图3所示)。

图3 路径覆盖度判定方法示意图

判定[X1, X2]是否满足k覆盖的具体方法如下：因为点(LPi,0)，(RPi,0)，∀1≤i≤Num，和端点(X1,0)，(X2,0)将线段[X1, X2]分成2×Num+1个小线段(包括长度为0的小线段)，如果这些小线段全部满足k覆盖，则[X1, X2]满足k覆盖。因此定义变量Cov_degree记录当前小线段的覆盖度，并将其初始值设为0。从X1开始检测每个小线段的覆盖度，如果当前小线段的右端点属于集合{LPi, 1≤i≤Num}，则下一小段的Cov_degree加1，否则减1。一旦出现Cov_degree＜k，并且当前段的长度不为0，则说明[X1, X2]不满足k覆盖。

下面以图3为例对上述方法进行说明，[X1, X2]在图3中被分成了5段，分别是[X1, LP1]，[LP1, RP1]，[RP1, LP2]，[LP2, RP2]，[RP2, X2]。Cov_degree的初始值设置为0，所以[X1, LP1]的覆盖度为0，但是由于[X1, LP1]的长度为0，所以不影响路径覆盖度的判定。线段[X1, LP1]的右端点LP1属于集合{LPi,1≤i≤2}，所以[LP1, RP1]的覆盖度为1，同理可以求得其余各小段的覆盖度。显然，由于[RP1, LP2]和[RP2, X2]的覆盖度为0，图3的目标路径不满足1覆盖。本文提出的映射检测法可以使路径覆盖度的判定摆脱2维坐标系的影响，从而简化计算的复杂度，同理也可以把路径映射到纵轴进行判定。

6 仿真结果

为了验证式(5)的正确性，本文采用MATLAB进行仿真，并将实验统计结果与理论分析结果进行比较。在仿真实验中，λ以0.2为步长由0变化到6，在每次实验中，节点按泊松分布随机布设在A=100 m×100 m的正方形区域，然后在其中随机地选择长度s=30 m的直线路径，并检测其是否满足k覆盖。仿真过程中，为了避免区域边界效应的影响，在选择直线路径的两个端点时使它们与边界的距离大于R。针对每个λ，该实验重复300次，并按下式计算路径满足k覆盖的概率：

下面分别给出节点感知半径服从不同概率分布时对第4节推导的理论分析结果的仿真验证。

6.1 节点感知半径相等

假设所有节点的感知半径都相等，即：感知半径都是R，这种感知模型也是覆盖问题的理论分析中使用最广泛的一种。根据第2节的定义有β=R，li服从如下概率分布：

可以很容易地求得a=E(l)=πR/2，将β和a的值代入式(5)得到如下式子

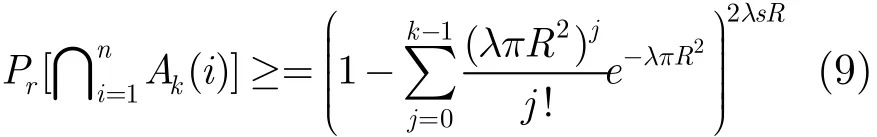
图4给出R=1 m时路径满足k覆盖的概率随λ的变化趋势。

6.2 节点感知半径服从均匀分布

假设节点的感知半径在[R/2, R]的区间内服从均匀分布，则有β=3R/4，li服从概率分布：

a=E(l)的具体数值可以用数值计算方法得到，图4给出R=1.5 m时路径满足k覆盖的概率随λ的变化趋势。

从图4和图5可以看出，在k值较小的时候，本文所给出的理论下界与实际仿真结果的差距较小。但是随着k值变大，理论值与实际仿真值的差距变大，这是因为随着k的变大，相邻Ak(i)，1≤i ≤n的相关性也在变大，使用FKG不等式所带来的误差也随之变大。另外，随着覆盖概率的变大，理论值与仿真值之间的差距呈现变小的趋势，考虑到在实际布设情况下，往往要求较高的k覆盖概率，且k值的设置不会很大，本文给出的分析结果对实际网络布设有着较为重要的指导意义。

图4和图5中分析结果与仿真结果偶尔有交叉，尤其是在k=1和k=2时，这是由实验样本的随机性及样本空间有限引起的，随着k的变大，由FKG不等式所带来的误差也随之变大，交叉也越来越少。

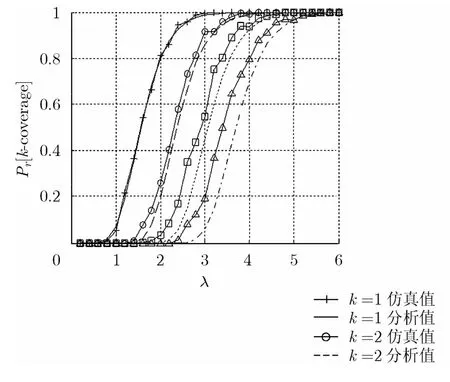
图4 节点的感知半径相等时路径满足k覆盖的概率随λ的变化趋势

图5 节点的感知半径服从均匀分布时 路径满足k覆盖的概率随λ的变化趋势

7 结论

本文对2维无线传感器网络中直线路径满足k覆盖的概率进行了建模分析，并给出其理论下界。给定路径满足k覆盖所需要的概率，由该下界求得的节点密度可以保证路径以不低于给定的概率满足k覆盖，而且从仿真结果中可以看出，在k值较小时，由该下界求得的节点密度与使路径以给定概率满足k覆盖所需的最小节点密度非常接近，因此本文的结果对网络规模的设置有重要的参考价值。

[1] Hall P. Introduction to the Theory of Coverage Processes[M].New York: John Wiley & Sons, 1988: 79-119.

[2] Shakkottai S, Srikant R, and Shroff N. Unreliable sensor grids:coverage, connectivity and diameter[C]. Proceedings of IEEE INFOCOM’03, San Francisco, CA, USA, Mar. 30-Apr. 3,2003: 1073-1083.

[3] Kumar S, Lai T H, and Balogh J. On k-coverage in a mostly sleeping sensor network[C]. Proceedings of ACM MOBICOM’04, Philadelphia, PA, USA, Sept. 26 - Oct. 1,2004: 144-158.

[4] Ram S S, Manjunath D, Iyer S K, and Yogeshwaran D. On the path coverage properties of random sensor networks[J].IEEE Transactions on Mobile Computing, 2007, 6(5):494-506.

[5] Manohar P, Ram S S, and Manjunath D. Path coverage by a sensor field: the nonhomogeneous case[J]. ACM Transactions on Sensor Networks, 2009, 5(2): 1-26.

[6] Harada J, Shioda S, and Saito H. Path coverage property of randomly deployed sensor networks with nite communication ranges[C]. Proceedings of IEEE ICC’08,Beijing, China, May 19-23, 2008: 2221-2227.

[7] Goldenberg D K, Bihler P, and Cao M, et al.. Localization in sparse networks using sweeps[C]. Proceedings of ACM MOBICOM’06, Los Angeles, CA, USA, Sep. 23-29, 2006:110-121.

[8] Sheu J, Hu W, and Lin J. Distributed localization scheme for mobile sensor networks[J]. IEEE Transactions on Mobile Computing, 2010, 9(4): 516-526.

[9] Kumar S, Lai T H, and Arora A. Barrier coverage with wireless sensors[C]. Proceedings of ACM MOBICOM’05,Cologne, Germany, Aug. 28-Sept. 2, 2005: 284-298.

[10] Saipulla A, Westphal C, Liu B, and Wang J. Barrier coverage of line-based deployed wireless sensor networks[C].Proceedings of IEEE INFOCOM’09, Rio de Janeiro, Brizil,Apr. 19-25, 2009: 127-135.

[11] Meester R and Roy R. Continuum Percolation[M].Cambridge: Cambridge University Press, 1996: 31-34.