3D-Wedgelet分解与工业CT体数据面特征提取

曾 理 李宗剑 刘长江

①(重庆大学光电技术及系统教育部重点实验室ICT研究中心 重庆 400044)②(重庆大学数理学院 重庆 400044)

③(重庆大学光电工程学院 重庆 400044)

④(四川理工学院数学系 自贡 643000)

1 引言

工业CT利用射线源在无损状态下对被检测材料进行射线扫描检测和图像重建，具有直观、可靠、灵敏度和分辨率高、影像不重叠等优点，被国际无损检测界誉为最佳的无损检测手段[1]。

工业CT体数据的主要特征由点、线、面、管状物和丝状物刻画[2]。其中，面特征常常对应目标对象的轮廓或边界面。抽取出工业CT体数据中的面特征对于描述和解译工业CT体数据本身是很重要的。

对体数据面特征的提取策略包括两大类：一类是直接对体数据进行面特征的提取；另一类是将体数据分解成一系列2D图像，对每幅2D图像进行线特征的提取，再将各幅2D图像的线特征组合成面特征。最经典的处理方法是边缘差分算子[3]，其它常见的方法如主动轮廓模型及其改进模型[4]、Facet模型[5]、基于小波的方法[6]等等。上述方法提取得到的面特征，其结果并不是直接描述面特征的方程，而是由一个个点特征组成，因此，只能从主观视觉效果上说得到了面特征。

多尺度几何分析是近十多年来，图像稀疏分解发展的一个分支，其非常适合检测、表示、处理某些类型的高维数据。Wedgelet变换作为多尺度几何分析方法家族中的一员[7]，由斯坦福大学的Donoho于1999年提出。Wedgelet以区域基的方式分析数据，对以不同灰度区域形式存在的边缘线和边缘面有很好的分析能力[8,9]。

2 离散3D-Wedgelet变换

Wedgelet被定义为N×N(N=2J)图像中被一条Beamlet分成的两块区域[10]，同理，3D-Wedgelet被定义为N×N×N(N=2J)数据中被一张Planelet分成的两块区域[11]，如图1所示。

2.1 3D-Wedgelet分解

记I为一N×N×N(N=2J)的体数据，Cj,k=表示尺度为j，位置为k=(k1, k2, k3)的立方体块，且0≤j≤J，0≤k1, k2, k3＜2j，j, k1, k2, k3∈Z。记Cj,k的边界点集为V(如图2黑点所示，其中，1小立方体块代表1体素)。任取不在同一边上的3点(v1, v2, v3)∈V，则平面将Cj,k划分成两块区域，两块区域的体素均值分别记为ma和mb，则立方体块Cj,k的3D-Wedgelet分解集W[ I(Cj,k)]为

图1 Wedgelet(a)和3D-Wedgelet(b)

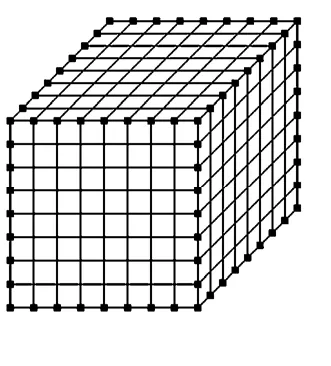
图2 立方体块中的边界点

2.2 快速3D-Wedgelet分解

对于N×N×N(N=2J)的立方体块，其边界点的个数为12N−4，理论上说，有张Planelet。但其中存在重复的情形，如图1(b)所示的Planelet包含了4个边界点，若按每3个边界点计算一张Planelet，则该Planelet将被计算4次。因此，若对立方体块中的每张Planelet直接进行计算，将存在大量的重复计算。鉴于此，考虑通过找出单尺度下不同Planelet间的内在联系，以实现减少3D-Wedgelet分解的计算量。

2.2.1 Planelet的形状 根据Planelet的边数，可将Planelet分为三边形、四边形、五边形和六边形4种，如图3所示。

图3 多边形Planelet

2.2.2 单尺度下Planelet间的联系 为讨论方便，建立如图4的坐标系，原点为立方体块的前左下顶点。

图4 坐标系

(1)三边形Planelet 三边形Planelet的3顶点相对位置关系只可能为图5所示的8种情形。

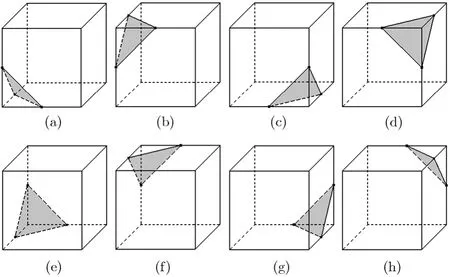
图5 三边形Planelet

设f(x, y, z)=0是图5(a)的一个三边形，则f(x, y, N−z)=0，f(N−x, y, z)=0，f(N−x, y, N−z)=0，f(x, N−y, z)=0，f(x, N−y, N−z)=0，f(N−x, N−y, z)=0，f(N−x, N−y, N−z)=0分别是图5(b)-5(h)的一个三边形。图5(a)中，三边形的3顶点坐标分别为(x1,0,0)，(0,y2,0)，(0,0,z3)。

(2)四边形Planelet 四边形Planelet包含两大类情况：一类是两组对边均平行；另一类是只有一组对边平行。构成四边形Planelet的立方体面可以是两组对面，也可以是相邻4个面，如图6所示，其中图6(a)-6(c)由两组对面形成，图6(d)-6(o)由相邻4个面形成。

对于由两组对面形成的四边形Planelet，设f(x, y, z)=0是图6(a)的一个四边形，则f(N−z,y, x)=0、f(x, N−z, y)=0分别是图6(b)，6(c)的一个四边形。图6(a)中，顶点A、B、C的坐标分别为(0,0,z1)，(N,0,z2)，(0,N, z3)。

对于由相邻4个面形成的四边形Planelet，设f(x, y, z)=0是图6(d)的一个四边形，则f(N−y,x, z)=0，f(N−x, N−y, z)=0，f(y, N−x, z)=0，f(x, N−z, y)=0，f(z, x, y)=0，f(N−x, z, y)=0，f(N−z, N−x, y)=0，f(x, N−y, N−z)=0，f(y, x,N−z)=0，f(N−x, y, N−z)=0，f(N−y, N−x,N−z)=0分别是图6(d)-6(o)的一个四边形。图6(d)中，顶点A，B，C的坐标分别为(0,0,z1)，(x2,0,N)，(0,N, z3)。

(3)五边形Planelet 五边形Planelet与立方体块的5个面相交，换句话说，只与1个面不相交，据此可粗分为6种情形。而对于每一种情形，又可细分为4种。设f(x, y, z)=0是图7的一个五边形，则f(N−x, y, z)=0，f(z, y, N−x)=0，f(z, y, x)=0，f(x, N−y, z)=0，f(N−x, N−y, z)=0，f(z,N−y, N−x)=0，f(z, N−y, x)=0，f(y, x, z)=0，f(y, N−x, z)=0，f(y, N−z, N−x)=0，f(y, N−z, x)=0，f(N−y, x, z)=0，f(N−y, N−x, z)=0，f(N−y, N−z, N−x)=0，f(N−y, N−z, x)=0，f(x, z, N−y)=0，f(N−x, z, N−y)=0，f(N−z, x, N−y)=0，f(N−z, N−x, N−y)=0，f(x, z, y)=0，f(N−x, z, y)=0，f(N−z, x, y)=0，f(N−z, N−x, y)=0分别是立方体中的一个不重复五边形。图7中，顶点A，B，C的坐标分别为(0,N,z1)，(x2,0,N)，(x3,0,0)。且x2≠x3，因为，若x2=x3，则为四边形Planelet。

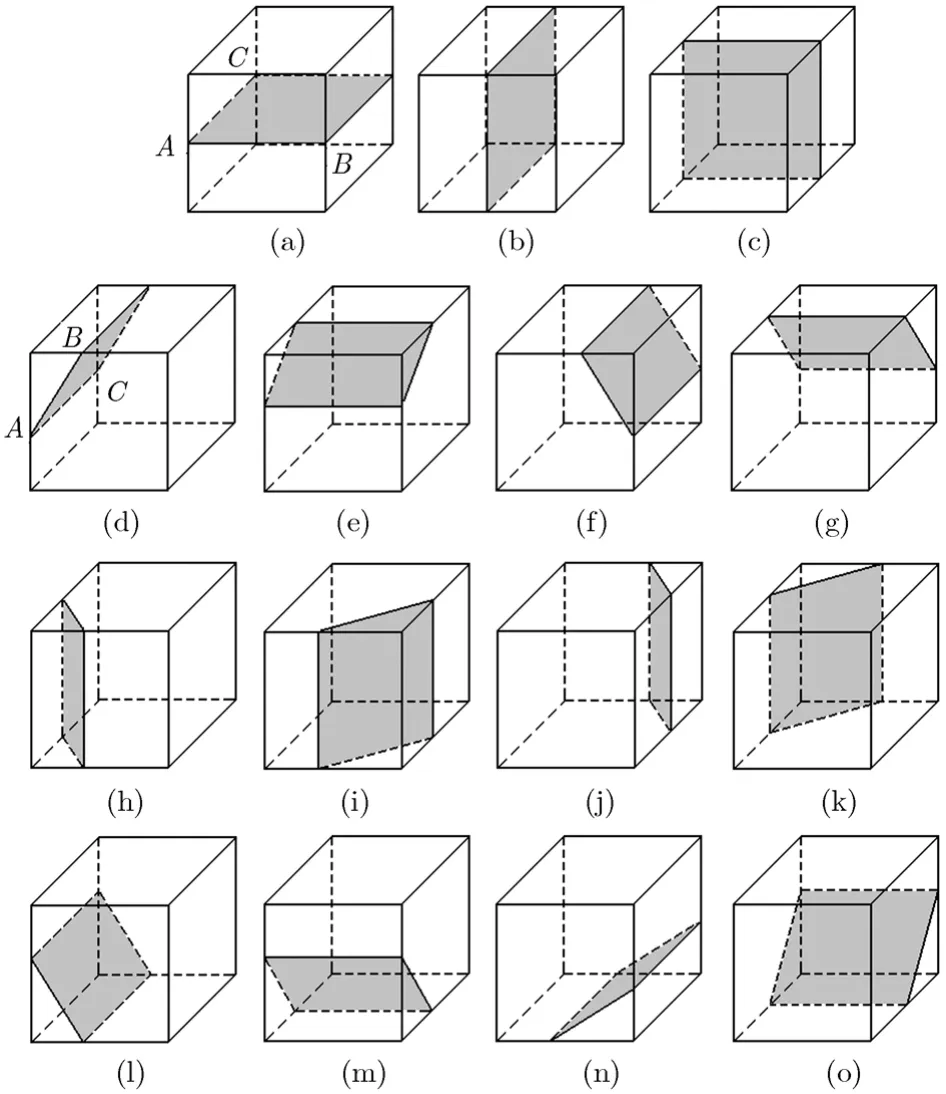
图6 四边形Planelet

(4)六边形Planelet 六边形Planelet与立方体块的6个面均相交，且3组对边两两平行，可以将其分为4种情形。设f(x, y, z)=0是图8的一个六边形，则f(N−y, x, z)=0，f(N−x, N−y, z)=0，f(y, N−x, z)=0分别是立方体中的一个不重复六边形。图8中，顶点A，B，C的坐标分别为(0,y1, N)，(x2,0,0)，(N, N, z3)。

图7 五边形Planelet代表

图8 六边形Planelet代表

2.2.3 单尺度下3D-Wedgelet的分解 记I0=被一张Planelet分开的两块3D-Wedgelet区域分别为w1, w2，各自的体素均值分别为m1, m2，包含的体素个数分别为N1, N2，N1+ N2=N3。

第1步 使用2.2.2节的方法，选定顶点A，B，C，计算平面Planelet的方程f(x, y, z)=0。

第2步 计算被平面f(x, y, z)=0分成的两块3D-We d g e l e t区域的体素均值m1, m2，m1=/N2。

第3步 利用2.2.2节讨论的坐标变换得到与该3D-Wedgelet区域相关的其它3D-Wedgelet区域，并计算出各自的体素均值。

重复上述步骤，依次计算完立方体内的三边形、四边形、五边形和六边形Planelet。

3 工业CT体数据面特征提取

对于立方体中的两互补3D-Wedgelet，按图4所示的x，y，z方向分别进行切片划分，均会得到一序列组的Wedgelet。因此，对于工业CT体数据面特征的提取，给出如下的两种思路：(1)基于3D-Wedgelet分解的提取方法；(2)先对体数据在x，y，z方向分别进行切片划分，然后对每张切片作基于Wedgelet分解的线特征提取，最后融合3个方向的线特征从而得到体数据的面特征。

3.1 单尺度下的特征提取

对于体数据而言，根据所选尺度j和位置k=(k1, k2, k3)，求出立方体块Cj,k内满足条件(t为阈值)的其中，m1, m2为由Planelet分成的两互补3DWedgelet的体素均值。对于切片图像而言，处理的思想一样。

3.2 多尺度下的特征提取

多尺度与单尺度相比，具有更大的灵活性。多尺度Wedgelet或3D-Wedgelet分解由不同尺度下的单尺度Wedgelet或3D-Wedgelet分解组成。经多尺度Wedgelet或3D-Wedgelet分解后的数据形成一种四叉树或八叉树结构。对四叉树或八叉树进行由下至上地最优修剪，就能得到线特征或面特征的最优表示。

由文献[11]知道：大尺度下的1条Beamlet，由小尺度下的1，2或3条Beamlet组成；大尺度下的1张Planelet，由小尺度下的1，2，3，4，5或6张Planelet组成。记大尺度下的正方形块为S，立方体块为C，小尺度下的正方形块分别为S1～S4，立方体块分别为C1～C8。沿用3.1节单尺度下的特征提取思想，给出多尺度下特征提取的判断条件。

对体数据而言，当

同时成立时，将C分解为C1～C8，其它情况则保留C。

对切片图像而言，当

同时成立时，将S分解为S1～S4，其它情况则保留S。

条件式(2)，式(4)说明子立方体块或图像块中存在比父立方体块或图像块中更明显的面或线特征。条件式(3)，式(5)保证了不会将1张大的面特征划分为多张小的面特征或1条长的线特征划分为多条短的线特征。

3.3 线特征的融合

考虑图9(a)中的体数据模型，背景为白色，目标对象为一实心立方体(为了视觉效果，用黑色标记出12条边)。记上，下，左，右，前，后表面分别为平面1，2，3，4，5，6。分别按x，y，z方向划分切片，切片图像均如图9(b)(含目标)和9(c)(不含目标)所示。对于这个体数据模型，我们感兴趣的面特征，实际上为立方体的6个面。

图9 体数据模型

若沿x，y，z方向分别划分切片，并进行基于Wedgelet的线特征提取，则提取结果分别是平面1，2，5，6；平面1，2，3，4；平面3，4，5，6。

从上面的分析可以看出，若按一个方向对体数据划分切片，最终得到的面特征提取结果将比实际感兴趣的面特征要少。因此，本文考虑将3个方向的提取结果进行数据融合。

记x，y，z方向各自的线特征提取结果分别为out_x，out_y，out_z。从上面的分析可以知道，若体素点v位于感兴趣的面特征上，则满足下式

即将3个方向上各自切片序列组的线特征提取结果进行合并，从而得到整个体数据的面特征。

但式(6)只是体素点位于感兴趣面特征上的必要条件，不是充分条件。对于实际的体数据而言，由于其结构组成更加复杂，利用式(6)得到的面特征中除了真正的面特征外还有一部分线特征，保留这部分线特征并不影响后续对体数据的分析。

4 实验结果与分析

实验的实际数据采用Internet上公布的工业CT体数据engine[12]，尺寸为256×256×128，其一张切片及3维显示分别如图10(a)，10(b)所示。实验用计算机配置如下：AMD3100+，1 G内存，VC++6.0，Windows XP。基于3D-Wedgelet和Wedgelet方法的分解尺度均为尺度4到尺度6，面特征提取结果的3维显示分别如图10(c)、10(d)所示，计算耗时分别为5507.320 s和1180.308 s。3维显示由3DMed软件[13]实现。

从图10(c)、10(d)中可以看出，本文的两种策略都是有效的。这是因为在工业CT体数据中，大部分的线特征和面特征并不是以独立的形式存在，而是表现为不同灰度区域的边界线或边界面。而Wedgelet或3D-Wedgelet基的表现形式为线(Beamlet)或面(Planelet)分开的两块区域，根据这两块区域的像素或体素均值，就能判断出该线或面是否为线特征或面特征。

图10 实验结果

从提取结果的主观效果上看，基于Wedgelet比基于3D-Wedgelet方法提取的面特征更平滑，尤其体现在曲面部分。出现这种结果有两方面的原因。一方面，基于3D-Wedgelet方法得到的面特征是由一系列的Planelet组成，而Planelet本身是平面，对体数据中曲面特征的描述实际上是一个平面逼近曲面的过程。另一方面，基于Wedgelet的方法是将面特征转化为3个相互垂直方向上的线特征进行提取。在转化的过程中同一张曲面经不同方向的划分后，有可能出现曲线，有可能出现直线。Beamlet本身是直线，对切片图像中曲线特征的描述实际上是一个直线逼近曲线的过程。但是融合3个相互垂直方向的线特征之后，会让这种逼近的痕迹减弱甚至消失。

从描述面特征的简洁性上看，基于3DWedgelet的方法得到的面特征是由一系列的平面(Planelet)方程组成，而基于Wedgelet的方法得到的面特征是由一系列的直线(Beamlet)方程组成，因此，前者对体数据面特征的描述会更简洁。

从计算时间上看，基于3D-Wedgelet方法的计算时间大致是基于Wedgelet方法的4.667倍。

5 结束语

本文先分析了单尺度下Planelet的组成及内在联系，得到了一种快速3D-Wedgelet分解方法。以此为基础，提出了分别基于3D-Wedgelet，Wedgelet的两种提取工业CT体数据中面特征的方法。实验结果表明，这两种方法都是有效的。如何更好地描述工业CT体数据中的曲面特征并减少计算时间，是下一步研究的重点。

[1] 曾理, 安贝贝, 马睿. 脊波在工业CT图像裂纹边缘检测中的应用. 仪器仪表学报, 2007, 28(6): 981-986.Zeng Li, An Bei-bei, and Ma Rui. Application of ridgelet in crack edge detection of ICT image. Chinese Journal of Scientific Instrument, 2007, 28(6): 981-986.

[2] 焦李成, 谭山. 图像的多尺度几何分析: 回顾和展望. 电子学报, 2003, 31(12A): 1975-1981.Jiao Li-cheng and Tan Shan. Development and prospect of image multiscale geometric analysis. Acta Electronica Sinica,2003, 31(12A): 1975-1981.

[3] 张丹丹. 基于边缘算子的结构损伤诊断方法研究. [硕士论文],湖南大学, 2008.Zhang Dan-dan. The studies on structural damage identification method based on edge operator. [MA.dissertation], Hunan University, 2008.

[4] Vasilache S and Najarian K. A unified method based on wavelet filtering and Active Contour Models for segmentation of Pelvic CT images. International Conference on Complex Medical Engineering, Tempe, Arizona, USA, April 9-11, 2009:1-5.

[5] 马睿, 曾理, 卢艳平. 改进的基于Facet模型的亚像素边缘检测. 应用基础与工程科学学报, 2009, 17(2): 296-302.Ma Rui, Zeng Li, and Lu Yan-ping. Improved sub-pixel edge detection method based on Facet model. Journal of Basic Science and Engineering, 2009, 17(2): 296-302.

[6] 胡正磊, 孙进平, 袁运能等. 基于小波边缘提取和脊线跟踪技术的SAR图像河流检测算法. 电子与信息学报, 2007, 29(3):524-527.Hu Zheng-lei, Sun Jin-ping, and Yuan Yun-neng, et al.. River detection in SAR images based on edge extraction in wavelet domain and ridge tracing technique. Journal of Electronics &Information Technology, 2007, 29(3): 524-527.

[7] Donoho D L. Wedgelet: nearly-minimax estimation of edges.Annals of Statistics, 1999, 27(3): 859-897.

[8] Liu Ze-yi, Sun Zi-qiang, and Xu Ling, et al.. Contour representation based on wedgelet. Journal of Systems Engineering and Electronics, 2006, 17(2): 251-257.

[9] Ren Chao, Wu Si-liang, and Jiao Li-cheng. Edge detection algorithm of SAR images with wedgelet filter. Journal of Beijing Institute of Technology, 2008, 17(3): 346-350.

[10] Donoho D L and Huo Xiao-ming. Beamlets and multiscale image analysis. Lecture Notes in Computational Science and Engineering, Berlin, Germany: Springer Press, 2001, 20:149-196.

[11] Ofer L. Multiscale geometric analysis of three-dimensional data. [Ph.D. dissertation], Scientific Computing and Computational Mathematics of Stanford University, 2005.

[12] General Electric. Engine. http://www.gris.uni-tuebingen.de/areas/scivis/volren/datasets/datasets.html.

[13] 中国科学院自动化研究所医学影像研究室. 3DMed. http://www.3dmed.net.Institute of Automation Chinese Academy of Science, Medical Image Processing Group. 3DMed. http://www. 3dmed.net.