基于改进二次误差测度及网格参数化的三维人脸本征属性描述方法

郭 哲 张艳宁 林增刚

(陕西省语音图像处理重点实验室西北工业大学计算机学院 西安 710129)

1 引言

近年来，随着计算、存储设备的飞速发展和3维数据采集技术的日益成熟，3维物体表面特征的有效描述，逐渐受到研究者的广泛关注[1]。以人脸特征为例，相对于2维图像而言，3维人脸数据包含了更多的空间形状信息，能从本质上克服2维人脸识别受光照、姿态变化的影响。但是，随着数据采集设备精度的不断提高，普通精度的人脸扫描数据也拥有几万到几十万个原始特征描述点，巨大的数据计算量所引发的算法效率问题成为制约3维人脸识别在实际应用中的主要瓶颈。因此，如何从高维数据中提取3维人脸的本征属性，降低特征描述的复杂度成为3维人脸数据应用的关键。

目前常用的3维人脸属性描述方法有基于曲率的描述方法[2]，局部几何属性描述方法[3]，区域描述法[4]以及形状变化模型[5,6]等。以上方法或采用局部属性描述，不能保证全局属性最优；或需要进行大量的参数估计，运算复杂；同时，以上方法都是在3维空间中对人脸表面特征进行描述，因此相对复杂度要高于简单的2维图像。

为了降低人脸数据在3维空间中的描述复杂度，同时获取与3维网格数据相应且最小信息丢失的2维图像描述，本文采用网格参数化方法对3维数据在2维平面上进行映射投影。由于3维激光扫描仪获取的人脸数据包含不规则三角网格，因此采用角度保持且能产生相对稳定结果的保形同构映射[7]来进行网格的参数化。另外，由于3维人脸模型通常具有较高分辨率，可以对其进行多分辨网格简化；同时人脸表面特征分布具有不均匀性，在眼睛、鼻子，嘴巴等五官区域集中了人脸最为重要的个性特征，而脸颊，额头等特征隐性区域则存在大量的冗余信息。因此，本文考虑对原始3维人脸网格模型进行以保持五官区域特征为前提的模型简化，用以提高计算效率。

基于以上分析，本文提出一种基于改进二次误差测度及网格参数化的3维人脸本征属性描述方法。首先，对基于二次误差测度(Quadric Error Metrics，QEM)[8]的模型简化方法进行分析，并对其进行改进，使其能够在保持人脸五官区域特性的前提下最大限度地简化模型；其次，借鉴多分辨分析的思想，利用改进的QEM方法得到原始人脸网格模型不同简化率的多分辨简化模型表示；然后，采用基于特征约束的保形同构映射网格参数化方法对3维网格数据在2维平面进行展开；最后，将3维人脸表面的本征属性在2维图像平面中进行离散化表示。通过对国际公共3维人脸数据库GavabDB[9]的特征可分性以及人脸识别实验，证明了本文提出的特征属性描述方法的有效性。

2 二次误差测度改进算法

2.1 二次误差测度算法描述

文献[8]提出基于QEM的边收缩算法，在生成高质量简化模型的同时，大大提高算法效率，成为改进渐进网格算法中最常用的一种误差测度。QEM算法使用边收缩操作生成的新顶点到相关三角平面距离的平方和作为误差度量，能够很好地保持模型的几何形状信息，因此理论上是一种非常完备的方法，能够对模型进行快速、高质量的简化。

但是，该算法存在以下缺陷，首先没有考虑模型的细节特征，在简化过程中会造成模型在保持较高整体几何相似度的同时，丢掉局部细节信息，如果直接将该方法用于人脸模型简化，模型表面的大量细节特征会发生变形甚至丢失；其次，由于该算法采用边收缩操作进行模型图元删除，并没有检测边折叠后三角形的形状及其合法性，因此采用QEM算法对模型进行简化时，多数情况下都会出现重叠三角形现象。这种重叠三角形的存在，产生了不合理的模型曲面形状，对进一步的模型简化和后续模型处理带来了巨大威胁。

2.2 改进算法描述

为解决QEM算法存在重叠三角形及丢失局部细节信息的问题，必须在边收缩操作之后对重叠三角形进行消除，同时修正模型顶点的误差度量方法，使其对人脸五官区域进行最大特征保持。基于以上思想，作者提出一种QEM改进算法，使用半边折叠操作消除简化中间模型中所存在的重叠三角形，同时建立基于曲率的自适应加权误差度量来保留模型的细节特征。改进算法的具体描述如下：

算法1 消除重叠三角形问题

(1)搜索边折叠后与vto相邻三角面中所有的重叠三角形；

(2)若存在重叠三角形，进入步骤3，否则退出；

(3)对于重叠三角形上的每一个顶点，若其相邻面全部都是重叠三角形，那么将其作为一个候选删除点；

(4)在所有的候选删除点中，选择邻接面数最少的一个顶点，作为当前边折叠的vfrom，选择vfrom的任意一个相邻顶点作为vto，collapse(vfrom,vto)；

(5)返回步骤1。

其中，vfrom及vto分别表示半边收缩操作中被删除和被保留的顶点；collapse(v1, v2)表示对v1、v2进行半边收缩操作。

算法2 特征保持的模型顶点误差度量

(1)计算人脸模型顶点曲率的变化范围，记作[cmin,cmax]；

(2)令

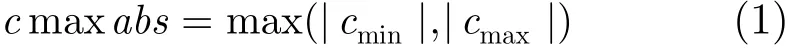
则模型顶点曲率的存在区间可记为[−cmaxabs,cmaxabs]；

(3)建立如下边收缩代价加权函数：

由此构造特征保持的顶点误差测度：

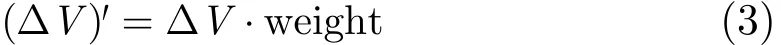
基于前述算法，改进的QEM算法流程描述如下：

(1)对模型中的每个顶点，根据算法2计算其收缩代价(ΔV)'；

(2)若S=φ或简化到指定结束条件，算法结束；

(3)取出顶点vmincost，collapse(vfrom,vto)；

(4)如果边折叠后vto的相邻三角面存在重叠，执行算法1；

(5)返回步骤(2)。其中vmincost表示当前模型中半边收缩代价最小的顶点；S表示三角网格模型；φ表示没有任何顶点和面片的空模型。

图1给出了一个3维人脸模型简化50%后的效果图。可以看出QEM算法的简化结果顶点分布比较均匀，没有突出保留特征区域，而改进算法的简化结果在人脸眼睛、眉毛、嘴巴、鼻子等五官特征区域的顶点比较密集，保留了原始模型的大量特征，而额头、腮部等特征不明显区域的顶点则得到更为充分的简化。由图1(c)，1(d)嘴部区域的比较可以看出，改进算法的简化结果在细节特征保持方面比QEM算法更加有效，细节更为丰富，具有更好的平滑性。

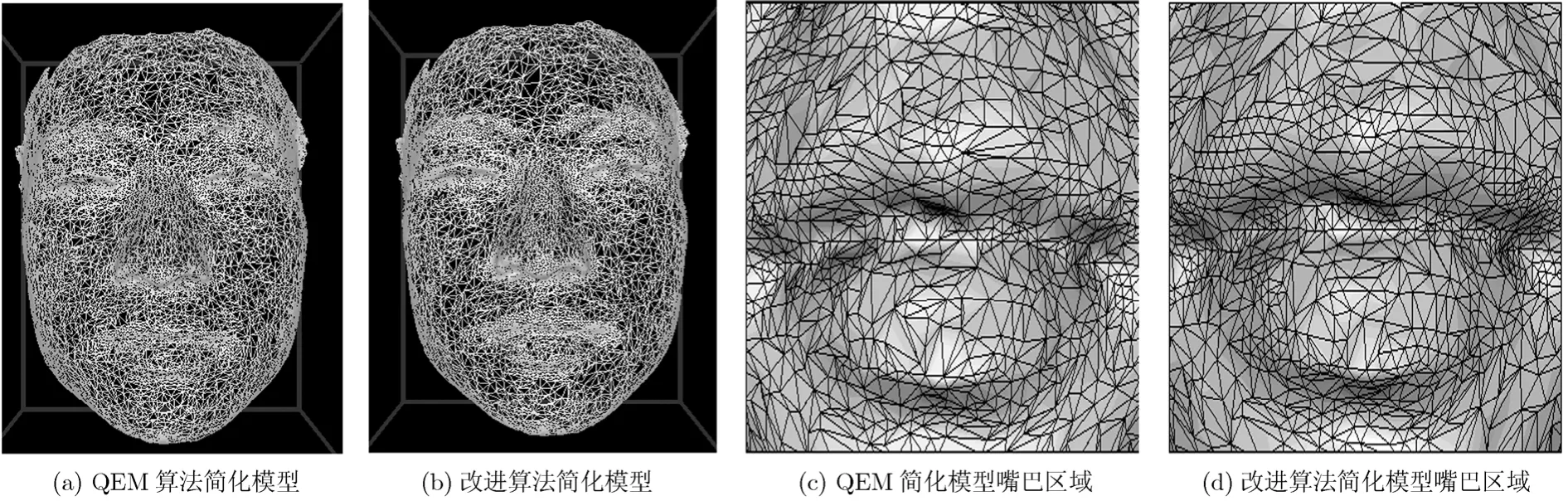
图1 3维人脸模型简化50%效果图

3 多分辨人脸本征属性描述图

3.1 特征约束的网格参数化

为了利用保形同构映射进行网格简化，需要建立3维人脸模型间的内在特征约束关系。首先选择人脸模型中曲率超过给定阈值[10]的点作为待选点，再通过比较这些待选点所对应的旋转图像(spinimage)[11]来检测特征相应性。由文献[1]可知采用spin-image特征进行匹配的结果对参数选择不敏感，因此文中通过经验确定的特征约束点为5,6个。

根据保形几何理论，一个圆周拓扑的3维表面能够通过全局优化同构映射到一个2维区域中[12]，这种映射可以是一对一，onto以及保形的。通过保形映射，3维人脸表面的每一个顶点都在2维平面上有唯一的一个对应点。本文通过Harmonic能量最小来完成保形映射[13]，并采用基准模型和特征约束点对人脸模型进行配准，最终得到有约束的保形平面展开。

不失一般性，本文考虑1环邻域(1-ring)情况[7]。假设S'为由3维空间中的1-ring邻域构成的简单网格，D'为S'的2维保形结构，如图2所示。如果映射边界固定，2维1-ring形变仅与中心节点ni相关。Dirichlet能量有着良好的角度保持特性，其能量函数为

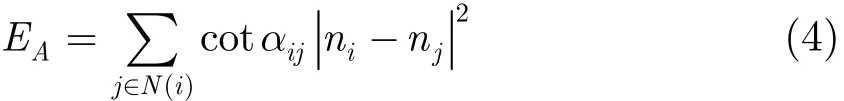
其中|ni−nj|表示D'中边(i, j)的边长，N(i)为节点i的1-ring邻接点，αij如图2所示夹角。令∂E/∂ni=0，则有如下公式：

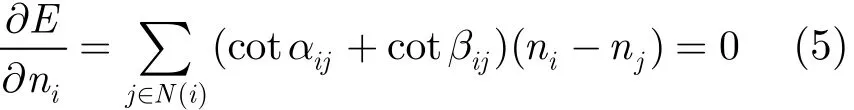
对于整个人脸表面，由式(5)可以推导出：

其中D为平面域的2维坐标向量，B为一个稀疏矩阵，可以表示为

图2 3维1-ring展开

此时，只要给定映射边界和相应的特征约束点，就能够得到对应的2维平面展开：

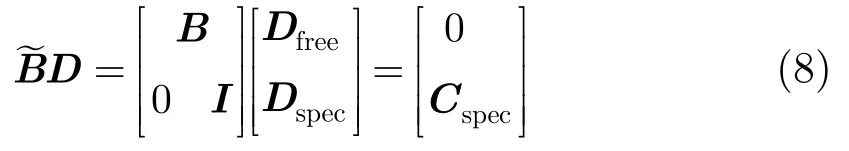
为了简便计算，D被分解为自由点集Dfree和指定点集Dspec两部分，该稀疏线性系统能够通过广义极小残差算法有效求解。图3给出了一组3维人脸模型的多分辨2维保形同构映射结果，文中，多分辨描述指原始精度3维人脸网格模型的不同简化率结果。

3.2 多分辨人脸本征属性描述图

对于3维人脸表面数据，首先借鉴多分辨分析的思想，采用本文2.2小节提出的改进二次误差测度算法对原始三角网格进行不同简化比率的网格简化操作，文中分别进行20%，50%，70%简化率的网格简化，得到原始网格数据相应80%，50%以及30%精度的多分辨描述；其次，分别对得到的多分辨描述数据，利用保形同构映射将3维空间表面数据映射到有约束的保形2维图像平面，如图3所示。

通过上述步骤，我们已经得到3维人脸表面的多分辨2维同构保形映射平面。此时，3维表面的多种不同本征属性，如：法线、曲率以及纹理等，都可以在2维图像平面中进行离散化表示，这个重采样过程可以通过对网格顶点像素属性值的插值来实现。本文选择离散均值曲率作为描述3维人脸表面的本征属性，并采用双线性插值方法来获取与3维人脸表面相应的2维本征属性图。图4给出了3维人脸表面的一组多分辨2维本征属性图描述。由图4(b)-4(e)可以看出，不同分辨率属性图都能有效描述曲率变化较大的面部五官区域，由于本文采用离散均值曲率作为属性值，曲率的估计会受到网格精度的影响，因此低精度属性图在非五官区域相对高精度属性图存在较多的噪声描述。

图3 基于保形同构映射的3维曲面展开结果(第1列为原始3维人脸模型，第2列至第5列分别为原精度，80%精度，50%精度，30%精度平面展开结果)

图4 3维人脸表面数据的多分辨2维本征属性图

4 基于本征属性的3维人脸模型匹配度量

在获得两个3维表面的2维属性图像后，3维表面的匹配问题就可以简化为2维平面的匹配，对于2维平面中的映射，本文采用将目标表面向参考表面的匹配通过匹配相应的离散平面属性图来实现。

给定两个有着圆周拓扑的表面S1和S2，首先通过spin-image来获取曲率变化较大顶点间的相应性，然后通过引入内部相应性作为约束，两表面相应的2维平面属性图能够通过第3小节的描述来获取。此时，两表面间的归一化相应性系数MS1,S2以及相似性度量S(S1, S2)[14]可以通过对相应2维平面属性图的计算获得：

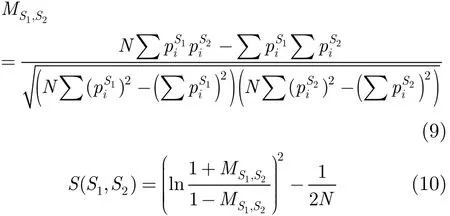
其中N为3维表面S1和S22维属性图中重叠部分顶点的个数，表示表面Sk2维属性图中顶点i的属性值，文中为离散均值曲率，k=1,2。由以上两式可知，两表面2维属性图相似度越高，MS1,S2越接近1，相应的S(S1, S2)值越大；反之，MS1,S2与S(S1, S2)均趋于0。

由于本文提出的人脸本征属性描述方法具有多分辨特性，因此对于每一种分辨率的属性图，就能够通过式(9)，式(10)获得一组度量值。由此，通过粗精结合的策略可以将本文提出的人脸本征属性描述方法有效地用于人脸配准以及识别。具体来讲，对于人脸配准应用，可以首先通过比较低精度属性描述图来获取较为准确的迭代初始参数，然后提高属性图的分辨率对参数进行逐级调整，最终达到理想的配准要求；同理，对于人脸识别应用，可以通过比较低精度属性图来排除大量干扰个体，有效缩小候选范围，提高精识别效率。

5 实验结果与分析

5.1 实验数据

本文采用国际公共3维人脸数据库GavabDB[9]进行测试实验。该数据库包含61个不同个体(45位男性，16位女性)的549个3维人脸扫描数据，仅有表面形状数据，不包括相应的纹理，每个个体包含9 幅不同姿态和表情的3维人脸数据，分别为：2幅正面中性表情，4幅中性表情但存在姿态变化的数据(左偏，右偏，向上，向下)以及另外3幅正面姿态具有表情变化的数据(微笑，大笑，任意表情)，所有被采集者均为白种人，年龄在18～40岁之间。对数据进行去除噪声，缺失区域补洞以及配准等预处理操作，获取实验所用人脸模型数据。实验主要测试本文提出的3维人脸本征属性描述方法的有效性，由于该方法不考虑表情变化属性，因此仅采用数据库中正面及姿态变化的中性表情数据，即61人的366个不同3维人脸数据。

5.2 实验结果与分析

本小节主要对本文提出的3维人脸本征属性描述方法的有效性进行测试，采用第4小节给出的归一化相应性系数以及相似性度量作为评估标准。由于实验数据中存在姿态变化造成数据缺失的情况，因此将实验数据分为正面无缺失数据子集(Frontal Neutral，FN)和多姿态缺失数据子集(Multi-pose Occlusion，MO)，分别采用两个不同子集对本文提出的方法进行鲁棒性测试。

5.2.1 相似度比较 本小节主要测试本文提出方法的有效性以及对数据缺失的鲁棒性，对于FN子集，分别计算同一个体两正面数据不同精度下2维属性图间的归一化相应性系数；对于MO子集，由于存在数据缺失，实验通过比较正面完整数据与多姿态缺失数据间的多分辨属性图归一化相应性系数来实现，平均匹配结果如图5所示，为了体现改进QEM算法的有效性，与原始QEM算法产生的属性图性能进行比较。由于保形同构映射对数据缺失造成的三角网格边界变化影响不大，同时，通过spin-image能够动态获取曲率变化较大顶点间的相应性以及两模型间的重叠顶点，因此FN子集与MO子集的平均匹配结果差别不大。改进的QEM算法能有效保留原始模型的重要五官区域特征，并对其他区域进行更充分的简化，因此基于改进QEM算法的本征特征描述平均匹配系数要高于基于原始QEM算法特征描述的结果。

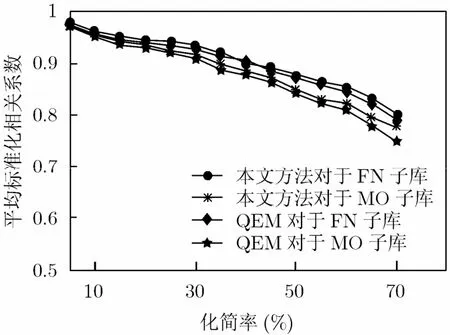
图5 2维本征属性图相似度比较

由图5可知，本文提出的基于改进二次误差测度及保形同构映射的属性描述方法能够有效描述3维人脸的本征属性，同时保持人脸重要的五官特征区域，并对精度变化不敏感，由于本文采用离散均值曲率作为网格顶点的属性值，离散曲率估计会受到网格精度的影响，因此低精度属性图的匹配结果要比高精度匹配结果逊色，但简化率 ＜30% 情况下的属性图之间结果差别不大。

5.2.2 识别率比较 本小节主要测试本文提出方法在人脸识别中的有效性，采用简化率20%的本征属性图，并与基准方法PCA以及基于曲率特征的方法进行比较。同样分别对FN和MO子集进行识别实验，对于FN子集，令其中一个正面中性表情人脸为训练样本，另外一个为测试样本；对于MO子集，仍然以一个正面中性表情人脸数据为训练样本，其他姿态变化数据为测试样本。使用最近邻分类及第4小节中的相似性度量测度来评估不同特征的可分性，实验结果如表1所示。

表1 rank-one识别率比较

由实验结果可知，本文提出的3维人脸本征属性方法具有良好的可分性，在FN数据集下的rankone识别率略高于基准方法PCA以及传统的基于曲率的方法。对于存在数据缺失的MO子集，由于PCA和曲率方法都是对原始3维空间点的几何特征进行描述，因此对数据缺失影响较大，识别率较低，仅为61.9%和75.2%；而本文方法采用对数据缺失造成的三角网格边界变化影响不大的保形同构映射来获取3维人脸本征属性的2维描述图；同时，通过spin-image所获取的特征相应性关系能根据模型表面形状变化进行动态调整，因此本文方法对数据缺失不敏感，对MO子集的rank-one识别率接近90%，远远高于PCA及曲率方法。

5.2.3 算法复杂度比较 3维人脸识别可有效提高人脸识别算法的鲁棒性，但是，巨大的数据计算量使得算法复杂度会显著增加，而在一些实时应用中，对算法的复杂度会提出较高要求。本文提出的方法通过多分辨网格简化及参数化技术将复杂的3维人脸识别问题简化为2维图像识别问题。为了分析本文算法的复杂度及高效性，分别计算本文方法100%精度、80%精度、50%精度下的本征属性图单次识别的时间，并与原始3维人脸模型曲率方法进行单次识别的耗时进行比较，实验结果如表2所示。

表2 不同算法效率比较

由实验结果可知，本文提出的多分辨3维人脸本征属性方法在算法复杂度方面相对于传统的基于3维数据的人脸识别有着较为明显的优势。100%精度2维本征属性图单次识别所需时间为0.715 s，相比原始3维人脸模型曲率方法的0.951 s，已有明显的提高。而80%精度和50%精度2维本征属性图在时间复杂度方面优势则更加明显，单次识别仅需0.504 s和0.297 s。因此本文方法在算法复杂度和时间效率方面有着较明显的优势。

6 结束语

本文基于模型简化及网格参数化思想，提出一种3维人脸数据在2维空间的本征属性描述方法。在该方法中，改进的基于二次误差测度的网格简化方法能有效保持人脸五官区域特征，并对其他区域进行最大限度的简化，降低数据冗余；保形同构映射方法能够将3维网格数据在2维平面进行保形展开。因此，本文方法得到的2维本征属性图在保持3维人脸表面属性的前提下，大大提高了计算效率。对GavabDB数据库的实验结果表明，本文方法对数据缺失鲁棒性较强，不同精度属性图的特征保持性差别不大；与PCA以及基于曲率方法的识别结果相比，本文方法对无缺失以及缺失数据集的rank-one识别率均明显高于基线算法。由于本文提出的方法具有多分辨属性，因此可以有效用于粗精结合的人脸配准及识别。同时，保形同构映射允许结合形状及纹理信息，本文方法可扩展应用于带纹理数据的3维人脸识别。

[1] Huber D, Kapuria A, and Donamukkala R, et al.. Parts based 3d object classification[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition,Washington, D.C., USA, June 27-July 2, 2004: 82-89.

[2] Lee Y and Marshall D. Curvature based normalized 3D component facial image recognition using fuzzy integral [J].Applied Mathematics and Computation, 2008, 205(2):815-823.

[3] AlOsaimi F R, Bennamoun M, and Mian A. Integration of local and global geometrical cues for 3D face recognition [J].Pattern Recognition, 2008, 41(3): 1030-1040.

[4] Berretti S, Alberto D B, and Pietro P. Analysis and retrieval of 3D facial models using iso- geodesic stripes[C].International workshop on Content-based multimedia indexing, London, June 18-20, 2008: 257-264.

[5] Sung Jaewon and Kim Daijin. Pose robust facial expression recognition using view-based 2D+3D AAM [J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A:Systems and Humans, 2008, 38(4): 852-866.

[6] Mayer C, Wimmer M, and Eggers M, et al.. Facial expression recognition with 3D deformable models[C]. 2nd International conferences on advances in computer human interactions,Cancun, Feb. 1-7, 2009: 26-31.

[7] Pan Gang, Han Song, and Wu Zhaohui. Hallucinating 3D facial shapes[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Anchorage, AK,June 23-28, 2008: 1-8.

[8] Garland M and Heckbert S. Surface simplification using quadric error metrics[C]. SIGGRAPH 97, Computer Graphics Proceedings, Annual Conference Series. Los Angeles, 1997: 209-216.

[9] Moreno A B and Sanchez A. GavabDB: A 3D face database[C]. 2nd COST Workshop on Biometrics, on the Internet, Vigo (Spain), March 2004: 75-80.

[10] Wang Sen, Wang Yang, and Jin Miao, et al.. Conformal geometry and its applications on 3D shape matching,recognition and stitching [J]. IEEE Transactions on Pattern Analysis Machine Intelligence, 2007, 29(7): 1209-1220.

[11] Johnson A and Hebert M. Using spin images for efficient object recognition in cluttered 3d scenes [J]. IEEE Transactions on Pattern Analysis Machine Intelligence, 1999,21(5): 433-449.

[12] Sheffer A, Praun E, and Rose K. Mesh parameterization methods and their applications [J]. Foundations and Trends in Computer Graphics and Vision, 2006, 2(2): 321-329.

[13] Desbrun M, Meyer M, and Alliez P. Intrinsic parameterization of surface meshes [C]. EUROGRAPHICS’02, Saarbrucken(Germany), Sep. 2-6, 2002: 210-218.

[14] Johnson A. Spin-images: A representation for 3D surface matching [D]. [Ph.D. dissertation], Robotics Institute, CMU,1997.