基于双树小波通用隐马尔可夫树模型的图像压缩感知

练秋生 王 艳

(燕山大学信息科学与工程学院 秦皇岛 066004)

1 引言

图像压缩感知(CS)是近几年图像处理领域的重大突破，它是由Donoho和Candes等人[1,2]在稀疏表示和优化理论的基础上提出的一种成像理论。其本质是直接将采样与压缩相结合，在对图像进行随机投影得到少量观测值后，利用图像表示的稀疏性先验知识，从观测值中恢复原始图像的过程。图像稀疏性是指其小波域只有少数与图像边缘纹理相对应的系数不为零或具有较大值，而与图像光滑部分相对应的大多数系数为零或近似为零。CS理论利用图像稀疏性先验知识，所需观测值远远小于Nyquist采样定理所要求的数目。目前的CS重构算法包括最优化算法和贪婪算法两大类。最优化算法将重构转化为特定优化问题，利用各类优化算法对其求解，常用算法有凸优化算法、非凸优化算法及光滑ℓ0范数(SL0)算法等。凸优化算法用ℓ1范数等价代替ℓ0范数，将重构转化为带约束的凸优化问题，然后求其最优解。迭代硬阈值法(IHT)[3]，凸集交替投影法(POCS)[4]，迭代加权法[5]等都属于此类算法。非凸优化算法[6]将ℓ0范数转化为ℓp(p＜1)范数，将重构转化为非凸优化问题，然后求其最优解，而光滑ℓ0范数法[7]则通过构建一个光滑函数来逼近ℓ0范数，然后对光滑函数进行优化实现重构。贪婪算法在每次迭代过程中选取一个或几个与观测值余量最大相关的基，寻找一组与观测值匹配的最稀疏基，从而实现信号的重构。匹配追踪(MP)、正交匹配追踪法(OMP)及它们的各种改进方法(如CoSaMP[8]，ROMP[9])均为此类算法。与传统基于Nyquist采样的重构相比，CS是一个重大突破。但标准CS重构只利用图像稀疏性先验知识，重构自由度大。实际上，图像的小波系数除具有稀疏性外，还具有一些结构上的分布特征，如与边缘纹理相对应的大系数往往呈树状分布，小波系数幅值在尺度间呈指数衰减等，将这些先验知识引入的CS重构中可改善重构效果，减少重构所需的采样值数目。Baraniuk在文献[10]中提出了基于模型的CS重构理论，证明了将描述信号小波系数分布的结构模型引入到CS重构理论的正确性及有效性，为基于模型的CS图像重构提供了理论依据。文献[11]提出了TMP(Treebased Matching Pursuit)和TOMP(Tree-based Orthogonal Matching Pursuit)算法，将信号小波系数呈树状分布结构用于MP或OMP算法中。这两种算法先利用MP或OMP算法寻找位于小波树顶端的大系数，然后沿着有大系数的子树向下搜索它的子系数，而对于没有大系数的子树不再进行搜索，与MP或OMP相比，此方法极大地缩小了搜索空间，减少了计算量，实现信号的快速重构。文献[12]提出了BOMP算法(Block-based Orthogonal Matching Pursuit)，将信号小波系数的块分布模型引入到OMP算法中。TMP,TOMP和BOMP算法相比与标准的CS重构有了较大改进，但上述算法引入的模型较为简单，不能精确刻画信号小波系数的结构分布特征，且上述算法对于一维信号的重构效果较好，但对于图像重构，算法计算开销大，重构效果不理想。图像小波域的隐马尔可夫模型(HMT)能较为精确地描述图像小波系数的分布特征，它已广泛应用于图像去噪[13]和图像复原[14]中。文献[15]将该模型引入到一维信号的CS重构中，采用重置权重的ℓ1范数最优化算法，直接将HMT模型参数引入的重置权重的修正中。但文献[15]未对算法的合理性做相应的理论推导，缺少理论依据。本文将HMT模型引入到图像的CS的重构中，从最大后验概率(MAP)出发，经过理论推导，将基于HMT的图像重构转化为与标准图像CS重构形式相似的优化问题，并提出采用基于贝叶斯优化的凸集交替投影法(Projections Onto Convex Sets，POCS)求解该优化问题。另外本文将具有更多方向选择性的双树小波域通用HMT(universal HMT，uHMT)模型代替小波域HMT模型，省去了使用HMT模型的计算开销巨大的训练过程。为进一步提高图像重构质量，本文对uHMT模型进行修正，提出了改进的uHMT模型(improved uHMT, iuHMT)，它能更精确刻画小波系数的局部分布特性，实验结果表明了算法的有效性。

2 稀疏变换域的uHMT模型及其改进

2.1 小波域HMT模型

图像的小波系数分布具有以下特征：(1)小波系数的非高斯性分布：即只有极少数小波系数具有较为显著的较大值，而绝大多数小波系数的幅值较小，近似为零。(2)小波系数状态的尺度持续性：小波系数“大”或“小”的状态具有在尺度间传递的特性。图像小波域HMT模型[14]能有效描述小波系数的上述特性。图像小波系数呈树状图分布，其HMT模型为每个小波系数wi设置对应的隐状态变量Si。HMT模型采用混合高斯模型来模拟小波系数分布的非高斯性：如果已知第i个结点隐状态变量的概率分布，则小波系数wi的概率密度与其他小波系数及隐状态变量无关，即式中pSi(m)=p(Si=m)为隐状态变量概率分布，它们满足为高斯概率密度函数，m为小波系数隐状态变量的一个实现，隐状态变量在1,…,M中取值，本文中M=2。m=1的高斯成分具有较小的方差，刻画与图像光滑部分对应的小波系数分布特征； m=2的高斯成分具有较大方差，刻画与图像边缘纹理对应的大系数的分布特征。

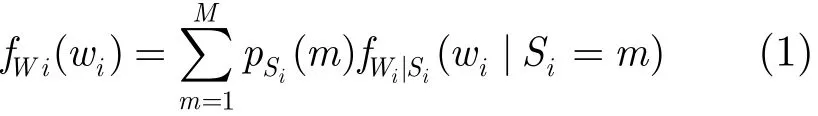
小波系数状态沿尺度的持续性可采用隐状态变量沿尺度的状态转移概率表征：任一结点小波系数的隐状态仅依赖于其父结点ρ(i)的隐状态，这种依赖关系由条件概率=p(m| S=r)来表Si| Sρ(i)ρ(i)征，它构成了此结点状态转移矩阵。上述参数、、μi,m、加上根结点处隐状态变量概率分布pS1(m)构成了HMT模型参数，记为θ。文献[16]假设同一级小波系数具有相同的模型参数，因此参数个数近似为4J(J为小波分解的级数)，它们可以通过EM算法训练得到。已知小波系数w和模型参数θ，可通过Upward-Downward算法获得小波系数的后验概率p(Si=m|w, θ)。在HMT模型下，由于小波变换的正交性，小波3个子带相互独立，小波系数的联合概率分布可表示为

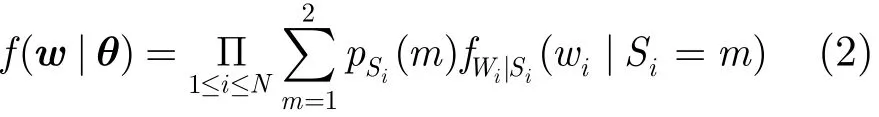
2.2 小波及双树小波域uHMT模型

上述HMT模型在使用中需经过大量的训练才能获得具体的参数值，计算量较大。文献[17]提出一种小波域通用HMT(universal HMT，uHMT)模型，它根据图像小波系数的幅值沿尺度呈现指数衰减特性得到HMT模型的各级高斯成分方差有以下关系：式中j表示小波变换级数，j=1,2,…,J 。小波系数的“大”或“小”的状态持续性沿尺度呈指数增强的特性，其状态转移矩阵可表示如下：

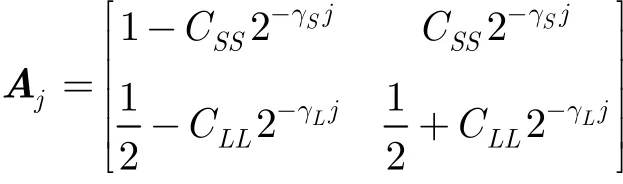
根据上述特性将HMT模型参数由原来的4J个减少为9个，即文献[17]提出的小波域uHMT模型参数为

该模型参数对于大多数自然图像都是适用的，因此用uHMT代替HMT能省去计算量较大的训练步骤，有效减少了计算开销。

普通的正交或双正交2维小波变换的方向选择性差(只有水平、垂直和对角线3个方向)，并且不具有平移不变性，它不能实现图像几何信息(如边缘和纹理)的最优表示。为提高图像压缩感知系统的性能，本文应用具有六方向选择性和平移不变性的双树小波[18]来实现图像稀疏表示。双树小波有实小波和复小波两种，为减少冗余度和计算量，本文应用冗余度为2的双树实小波。双树小波的uHMT模型参数与小波uHMT模型参数类似，经过对多幅图像的训练获得双树小波域uHMT模型参数为

2.3 改进的uHMT(iuHMT)模型

上述uHMT模型将同级所有小波系数的uHMT模型的高斯成分简化为具有相同的方差。然而由于小波系数的分布具有局部性，不同子带不同位置的高斯成分方差并不相同，且成分方差与小波系数的局部能量相关。基于这一特性本文提出了局部自适应性的改进uHMT模型(iuHMT,improved uHMT)，将高斯成分的方差与小波系数的局部能量相关联。设w为图像小波系数或双树小波系数，图像的噪声为2σ，则某点处小波系数wi的局部能量表示为：，其中Ni是以i点为中心的邻域，M为邻域大小，本文取M=3×3。wi两个高斯成分的方差可分别表示为：则iuHMT模型的参数可改为：θ=。其中参数kS和kL分别表示两个高斯成份的方差与该点小波系数局部能量的比例关系。通过对多幅图像的统计结果，kL为0.1，kS分别为0.2和0.25时小波与双树小波域的iuHMT性能最好。本文中小波域的iuHMT模型的参数取值为

双树小波域的iuHMT模型的参数取值为

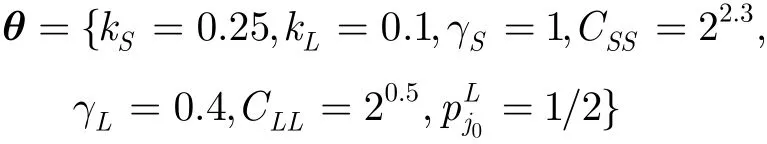
iuHMT的模型参数比uHMT少两个，并且由于高斯成分的方差具有局部性和自适应性，它能更精确描述小波或双树小波系数的分布特征。

3 基于双树小波uHMT模型的压缩感知图像重构

3.1 图像压缩感知

设信号x的稀疏变换为x=Ψw，Ψ为信号的稀疏基，w为信号的稀疏系数。采用投影矩阵Φ对信号进行投影，得到信号的观测值y=Φx。理论证明只要Θ=ΦΨ满足限制等容性[1,2](Restricted Isometry Property, RIP)，利用观测值y，即可重构信号x。信号x的重构可表示为求解以下优化问题：

式中η为观测噪声。式(3)表示在满足观测值条件下，寻找x的非零变换系数最少的解，即x的最稀疏解。由于上述优化问题是一个典型的NP-hard问题，通常采用ℓ1范数等价代替ℓ0范数[1,2]，即优化问题式(3)等价为

求解上式的典型算法包括迭代硬阈值法(IHT)和迭代软阈值法(IST)。

3.2 重构模型的推导

引入HMT模型后，根据最大后验概率(MAP)准则，压缩感知图像重构可表示为

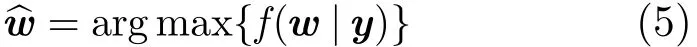
式中f(w| y)为小波系数的条件概率密度，y=ΦΨw +η为图像x的观测值，η为高斯白噪声：η～N(μ, σ2)。根据贝叶斯公式式(5)等价为

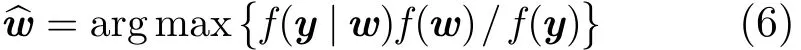
式中f(w)和f(y)分别为w和y的概率密度函数，f(y)为常数，f(w)即为式(2)表示的HMT模型的联合概率密度函数。由于η=y−ΦΨw 为高斯分布，因此有

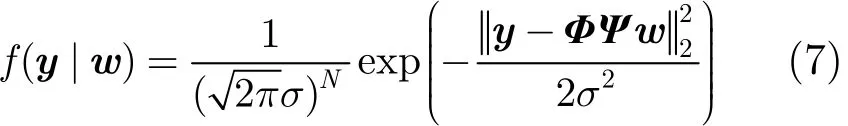
对式(6)右端取自然对数得

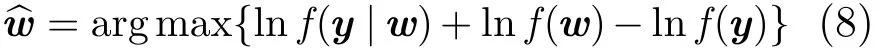
将式(2)，式(7)代入式(8)并去掉常数项得

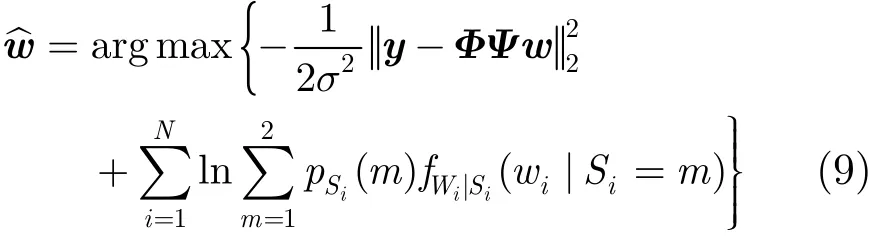
将式(9)的右边乘−1有

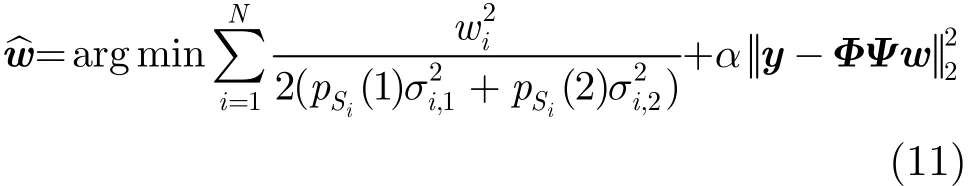
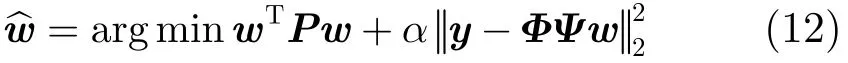
根据拉格朗日乘子法，式(12)可以写成下列形式：

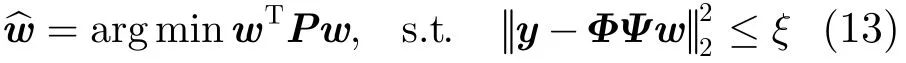
式(13)与式(4)类似，均为在满足观测值条件下寻找满足要求的最优解，关键区别为式(4)是只利用了信号的稀疏性先验知识，而式(13)则包含了HMT模型蕴含的稀疏性和树结构分布先验知识。

3.3 重构算法的实现

式(13)为凸优化问题，本文采用基于贝叶斯优化的凸集交替投影(POCS)算法求解，优化问题涉及以下两个凸集：

POCS算法交替向两个凸集C1和C2进行投影， C1和C2的交点即为式(13)的最优解：

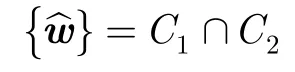
POCS算法迭代步骤如下：

(1)将第t次迭代的结果wt向C1投影：

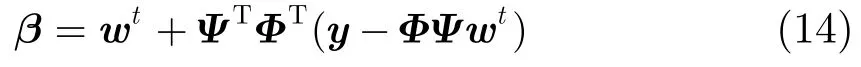
(2)利用梯度下降法将β向C2投影：

梯度下降法需在每次迭代中在下降方向上寻找最优步长，即进行一次线性优化搜索，计算开销较大。本文采用贝叶斯优化[17]代替梯度下降法。令λ=diag(λi)，其中λi为

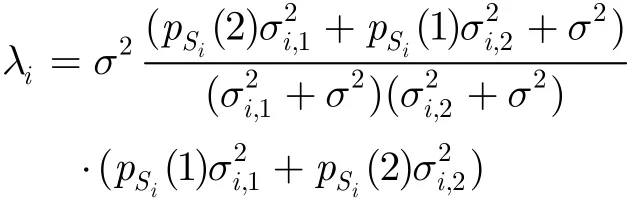
根据式(15)得到t+1w的第i个分量为

将λi的值代入并化简得

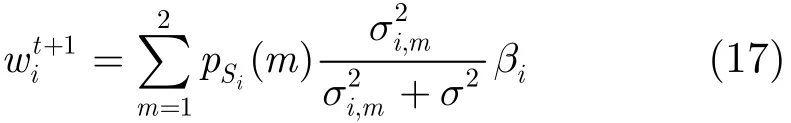
式(17)即为文献[17]给出的HMT模型的贝叶斯优化结果。贝叶斯优化方法根据模型参数，对系数进行统计优化 ，避免了每次迭代过程对步长的优化搜索，减小了计算量。

基于双树小波iuHMT模型的压缩感知重构算法具体步骤包括：

(1)初始化：设置最小误差Emin和最大迭代次数tmax, w1=ΨTΦTy ，t=1。

(2)利用式(14)将wt投影到C1得到β。式中Φ表示PDCT(Permuted Discrete Cosine Transform)投影，Ψ和ΨT表示双树小波变换及其逆变换。

(3)利用稳健中值算子估计β所含噪声的方差σ2。

(4)利用双树小波域iuHMT模型参数及Upward-Downward算法估计β的隐状态变量后验概率pSi(m)。

(5)将β投影到C2，即利用式(17)获得wt+1。

(6)xt+1=Ψwt+1，若||xt+1−xt||＜Emin或t＞tmax则转移到下一步，否则令t=t+1转到(2)继续执行。

(7)输出重构图像xt+1。

4 实验结果

为验证算法有效性，本文将基于uHMT模型和iuHMT模型的图像压缩感知重构与标准的图像压缩感知重构算法进行比较。本文实验选取barbara,boat, couple, hill, lena, man, fingerprint 7幅512×512的标准灰度图像进行重构。实验中分别用DWTIHT, DWTuHMT, DWTiuHMT, TDWTIHT,DTDWTuHMT, DTDWTiuHMT表示小波域的IHT重构、小波域uHMT模型重构、小波域iuHMT模型重构、双树小波域IHT重构、双树小波域uHMT模型重构及双树小波域iuHMT模型的重构。其中小波域的uHMT及iuHMT重构算法将上部分算法实现中步骤(2)的双树小波变换改为Daubechies4正交小波变换，步骤(4)中的参数相应改为小波域的模型参数值。

表1为DWTuHMT、DWTiuHMT和DWTIHT算法在不同采样率下重构的峰值信噪比(PSNR)比较。表中平均值一栏为各算法在各个采样率下7幅图像重构PSNR的平均值，黑体数字表示较高的PSNR。由表1可以看出在采样率为20%，30%和40%时DWTuHMT算法重构的PSNR平均值要比DWTIHT算法的PSNR平均值分别高出1.39 dB,2.12 dB和2.50 dB，DWTuHMT算法重构效果明显优越于DWTIHT算法；在采样率10%，DWTuHMT相比DWTIHT高出0.25 dB。在4种采样率下，DWTiuHMT重构的PSNR平均值较DWTIHT分别高5.31 dB，5.34 dB，5.24 dB，4.93 dB，较DWTuHMT分别高5.06 dB，3.95 dB，3.12 dB，2.43 dB，充分体现了基于iuHMT模型重构的优越性。表2 为DTDWTuHMT, DTDWTiuHMT和DTDWTIHT算法对7幅图像重构PSNR平均值的比较。从表2可以看出在采样率为20%、30%、40%时，DTDWTuHMT算法重构PSNR平均值比DTDWTIHT算法分别高出1.03 dB，1.51 dB，1.74 dB。在4种采样率下，DTDWTiuHMT重构的PSNR平均值比DTDWTIHT分别高出了1.30 dB，2.46 dB，2.39 dB，2.20 dB之多，较DTDWTuHMT也分别高出了1.13 dB，1.43 dB，0.88 dB，0.46 dB。基于DTDWTiuHMT模型的重构图像PSNR的平均值比DTDWTuHMT模型高0.97 dB，同样体现了基于iuHMT模型重构算法的优越性。将表1中DWTuHMT、DWTiuHMT算法对各图像的重构PSNR与表2中DTDWTuHMT, DTDWTiuHMT算法对各图像的重构PSNR进行比较可以看出，DTDWTuHMT在4种采样率下重构PSNR平均值比DWTuHMT分别高出4.82 dB，4.17 dB，3.32 dB，2.47 dB；DTDWTiuHMT的重构PSNR平均值比DWTiuHMT分别高出了0.89 dB，1.65 dB，1.06 dB，1.50 dB，充分表明双树小波比普通小波更适合于压缩感知。

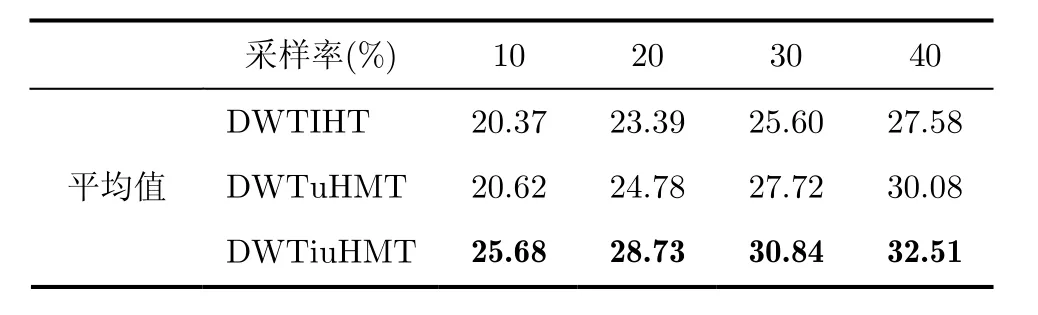
表1 小波域uHMT、iuHMT重构与IHT重构PSNR的比较

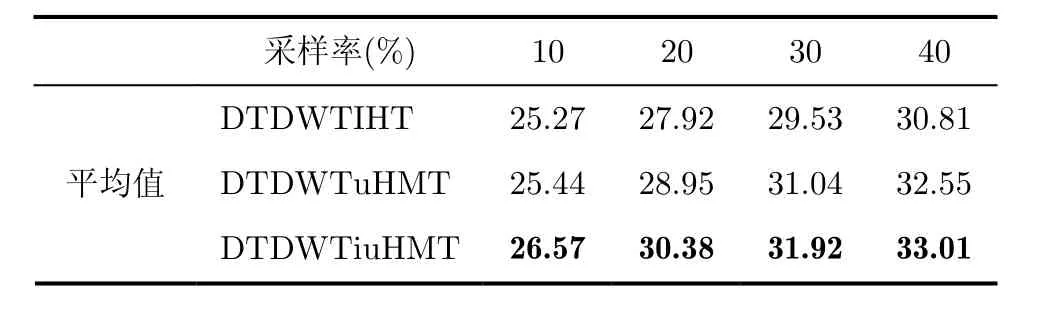
表2 双树小波域的iuHMT、uHMT重构与IHT重构PSNR的比较

图1为采样率为20%时各种算法对barbara重构结果的局部图像。图1(a)为小波域IHT算法重构的图像，该图像纹理信息丢失严重，且含有大量噪声；图1(b)为小波域的uHMT模型重构图像，与图1(a)相比，该图像恢复了更多的纹理信息，重构效果有明显改善；图1(c)为小波域的iuHMT模型重构图像，与图1(a)，1(b)相比，纹理信息进一步增多，且所含噪声进一步降低；图1(d)为双树小波域的IHT重构图图像，它恢复了较多的纹理信息，但图像过度平滑，造成模糊失真；图1 (e)为双树小波域uHMT算法的重构图像，包含了更丰富的纹理信息，图像更清晰，有效改善了图1(d)的模糊失真；图1(f)为双树小波域iuHMT算法的重构效果图，与其余5幅图像相比，它的纹理和边缘信息最清晰，视觉效果最好。

5 结论

标准的压缩感知重构只是利用了小波系数稀疏性的先验知识，而未利用小波系数分布结构特征的先验知识。本文提出一种基于双树小波域改进uHMT模型的图像压缩感知重构算法，将有效描述图像小波系数分布的HMT模型引入的图像的压缩感知重构。从最大后验概率出发，经过理论推导，将基于HMT的重构转化为型如标准压缩感知重构的优化问题，并提出采用基于贝叶斯优化的POCS算法对优化问题求解。本文还提出了基于双树小波域的uHMT模型，与小波相比，双树小波能更加有效地描述图像的几何信息，且采用uHMT模型省去了HMT模型所需的计算量巨大的训练过程，提高了重构质量和重构速度。另外本文对uHMT进行了改进，提出参数个数更少，更能精确描述双树小波变换系数分布特征的iuHMT模型，进一步提高了图像重构质量。

图1 采样率为20%时barbara重构效果比较

[1] Donoho D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[2] Candes E J nd Romberg J T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[3] Blumensath T and Davies M E. Iterative thresholding for sparse approximations[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 629-654.

[4] Bregman L M. The method of successive projection for finding a common point of convex sets [J]. Soviet Math, 1965,6(3): 688-692.

[5] Chartrand R and Yin Wotao. Iteratively reweighted algorithms for compressive sensing[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 2008: 3869-3872.

[6] Chartrand R. Exact reconstruction of sparse signals via nonconvex minimization [J]. IEEE Signal Processing Letters,2007, 14(10): 707-710.

[7] Mohimani G H, Babaie-Zadeh M, and Jutten C. A fast sparse approach for overcomplete sparse decomposition based on smoothed ℓ0norm [J]. IEEE Transactions on Signal Processing, 2009, 57(1): 289-301.

[8] Needell D and Tropp J A. CoSaMP: Iiterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2008, 26(3): 301-321.

[9] Needell D and Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics, 2009,9(3): 317-334.

[10] Baraniuk R G, Cevher Volkan, and Marco T D, et al..Model-Based compressive sensing [J]. IEEE Transactions on Information Theory, 2010, 56(4): 1982-2001.

[11] Duarte M F. Fast reconstruction from random incoherent projections[R]. Rice ECE Department Technical Report Tree,2005.

[12] Yonina C E and Helmut B. Block-sparsity:coherence and efficient recovery[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan,2009: 2885-2888.

[13] Kivinen J J, Sudderth E B, and Jordan M I. Image denoising with nonparametric Hidden Markov trees[C]. IEEE International Conference on Image Processing, San Antonio,Texas, 2007, 3: 121-124.

[14] 赵书斌，彭思龙. 基于小波域HMT模型的图像超分辨率重构[J]. 计算机辅助设计与图形学学报，2003, 15(11): 1347-1352.Zhao Shu-bin and Peng Si-long. Wavelet-domain HMT-based image superresolution[J]. Journal of Computer-aided Design& Computer Graphics, 2003, 15(11): 1347-1352.

[15] Marco F D, Wakin M B, and Baraniuk R G. Wavelet-domain compressive signal reconstruction using a hidden markov tree model[C]. IEEE International Conference on Acoutics,Speech and Signal Processing, Las Vegas, NV, USA, 2008:5137-5140.

[16] Crouse Matthew S, Nowak R D, and Baraniuk R G. Waveletbased statistical signal processing using Hidden Markov Models[J]. IEEE Transactions on Signal Processing, 1996,3(6): 1029-1035.

[17] Romberg J K, Hyeokho C, and Baraniuk R G. Bayesian tree-structured image modeling using wavelet-domain hidden markov models [J]. IEEE Transactions on Image Processing,2001, 10(7): 1056-1068.

[18] Selesnick I W and Baraniuk R G. The dual-tree complex wavelet transform[J]. IEEE Signal Processing Magazine, 2005,22(6): 123-151.