一种基于概率密度传播的目标跟踪算法

高庆华 金明录 王 洁 王洪玉

(大连理工大学电子与信息工程学院 大连 116023)

1 引言

目标跟踪问题是WSN(Wireless Sensor Network)领域的研究热点。有效的目标跟踪是无线传感器网络在战场信息监测、生活习性监测、室内定位等众多领域得以应用的基础。目标跟踪算法整体上分为两大类：一类是概率方法，将跟踪问题转化为状态估计问题，采用贝叶斯估计、极大似然估计等方法处理问题；另一类是数值方法，将跟踪问题看作优化问题，采用求极值的方法处理问题。在目标运动轨迹没有规律、系统噪声和观测噪声较复杂的情况下，基于概率的方法通常具有较强的鲁棒性和较优的跟踪精度。

近年来，PF(Particle Filter)算法被提出并用来解决非线性、非高斯环境下的目标跟踪问题。PF算法理论上基于后验分布进行采样，实际应用中很难实现对后验分布直接采样，因此通常基于先验分布采样，然后利用似然函数进行加权，这样处理造成当前时刻的观测信息在采样中没有发挥作用，当先验分布与似然函数偏差较大时，会造成绝大多数粒子权值趋近于零的退化现象发生，文献[1]证明随着时间的推移这种退化必然发生。一种直观的克服该问题的方法是增加粒子数目，但这样势必造成计算量的增加。重采样可以在一定程度上缓解该问题，但会造成粒子多样性降低，易发生粒子耗尽、贫化问题。Doucet提出采用扩展卡尔曼滤波算法对每个粒子进行预测；文献[2-4]等人提出基于无迹卡尔曼滤波算法对每个粒子进行预测；文献[5,6]提出采用高斯函数对粒子进行平滑处理；文献[7]等提出利用观测到的参考节点信息对预测粒子进行mean-shift偏移；文献[8]提出利用参考节点信息构建目标可能出现区域的方法对粒子采样区域进行限制；上述算法优化了提议分布，使先验分布与似然函数的交集变大，一定程度上克服了粒子退化问题，但是，这类算法本质上仍然需要对概率密度分布进行采样，不能彻底摆脱粒子退化、贫化的问题。文献[9]提出一种采用连续函数表征目标分布的算法实现人脸跟踪，有效地克服了PF算法采样困难的问题，但是该算法通过多次采样、拟合获得似然函数，需要计算大量Hessian矩阵、求逆矩阵等复杂操作，不适用于WSN。

针对上述问题，本文提出一种贝叶斯框架下的概率密度传播跟踪算法PDPA(Probability Density Propagation Algorithm)，采用高斯混合模型来表征目标概率分布，通过对连续函数的一系列操作实现目标跟踪，解决了大噪声、非线性、非高斯环境下基于WSN的目标跟踪问题。

2 系统模型

PDPA算法基于贝叶斯框架，采用状态空间模型来表述WSN跟踪问题，令目标的状态变量序列为{xt, t=1,…,N }，观测变量序列为{zt, t=1,…,N}，则有

这里F为状态预测函数，H为状态观测函数，wt为过程噪声，vt为观测噪声。

在预测方程和观测方程的作用下，状态分布先验概率密度函数p(xt|z1,…,t−1)和后验概率密度函数p(xt|z1,…,t)按式(3)，式(4)进行状态预测和更新：

状态转移概率函数p(xt|xt−1)由式(1)确定，观察似然概率函数p(zt|xt)由式(2)确定。

GMM(Gaussian Mixture Model)具有近似表示任意概率分布的能力，文献[10，11]对此作了详细研究，本文亦采用GMM来表示概率分布函数如式(5)所示。

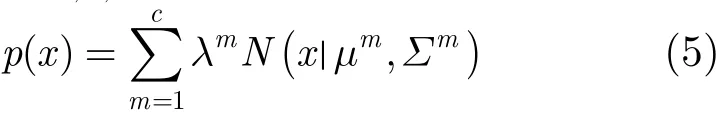
这里c为高斯核个数，λm为第m个核的权值，μm为其均值，Σm为其方差，高斯函数定义为

这里d为变量x的维数，文中T代表转置。

3 概率密度传播跟踪算法

PDPA算法采用GMM表征先验分布、似然函数、后验分布，有效地克服了PF算法退化、贫化、采样效率低的问题，同时，具有处理非线性、非高斯问题的能力。整个算法基于贝叶斯框架，分为预测、似然函数构建、后验分布计算、目标位置确定4部分。

3.1 预测

这里Σw用于补偿运动噪声。对GMM中每个高斯函数均进行UT变换，获得的先验分布如式(10)所示

3.2 似然函数构建

当目标探测到的参考节点个数k≥2时，假设获得的参考节点位置、距离信息集合为为参考节点i的位置，di为其与目标的距离，任意两个参考节点{i, j| i∈之间的距离dij=如果满足约束条件(di+dj则求解以(xi, yi)为圆心di为半径的圆与以(xj, yj)为圆心dj为半径的圆的交点，将求得的交点作为GMM模型的均值，观测噪声的方差作为GMM模型的方差，权值为交点总个数的倒数。

当未收到参考节点信息时，令似然函数为常数1。

3.3 后验分布计算

后验分布函数为先验分布函数与似然函数的乘积，如式(11)所示

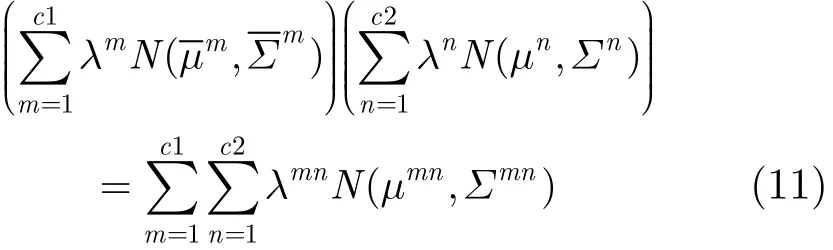
这里c1为先验分布核个数，c2为似然函数核个数，相乘得到核个数为c1×c2的GMM函数，新GMM参数如下

新的GMM函数综合了先验信息以及当前时刻的观测信息，代表了目标的后验分布信息。但是，直接将该函数作为后验分布势必造成GMM函数中核个数随时间不断增加，导致算法计算量灾难性增长。本文采用以下3种方法对新GMM函数进行拟合处理，以确保后验分布核个数的恒定。

方法1 基于核系数选择 直接选择模型中系数最大的c1个核构成新的GMM函数。

方法2 EM拟合 首先，对c1×c2个样本点μmn进行重采样，各样本点被选择的概率正比于λmn−1，重采样获得样本集{s, i=1,…,N }，通i常令样本个数N=10×c1×c 2。然后，采用EM算法对这些样本点的分布进行拟合处理，转化为具有c1个核的GMM函数，EM算法分为E-step和M-step两个步骤。

E-step：

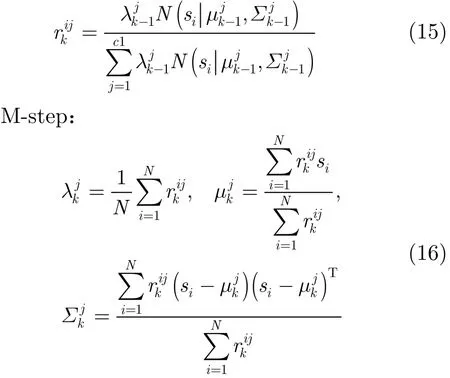
方法3 K-mean拟合 与EM算法相比，K-mean算法具有简单、计算量小的优点。算法首先从c1×c2个权值为的样本点mnμ中随机选取c1个点作为聚类中心，然后，根据各样本点与各聚类中心的欧式空间距离对样本点分类，计算各类样本点的加权质心作为新的聚类中心。此过程进行多次后收敛，此时聚类样本的聚类中心、方差、样本个数占总样本个数的比例即为GMM模型中的均值、方差与权值。

拟合处理后的后验分布GMM函数为

3.4 目标位置确定

PDPA算法将后验分布p(x)各高斯核均值的加权质心作为当前时刻的目标位置，如式(18)所示

整个PDPA算法遵循贝叶斯框架，基于上一时刻的后验分布进行预测，获取当前时刻的似然函数，然后求解当前时刻的后验分布，同时，计算后验分布中各模式的加权质心并将其作为当前时刻的位置。算法初始时刻直接将似然函数确定的位置作为其估计位置。

4 性能仿真与分析

4.1 仿真模型与环境

实验中目标基于CV/CT混合模型运动，具体模型参见文献[12]。运动噪声与观察噪声均为对称双峰非高斯噪声，运动噪声模型为w1N(μ1, Σ1)+(1−w1)N(−μ1, Σ1)，运动噪声均值默认为μ1=1，方差Σ1=1，系数w1∈[0.2,0.8]；观察噪声模型为w2N(μ2, Σ2)+(1−w2)N(−μ2, Σ2)，观察噪声均值默认为μ2=20，方差Σ2=20，系数w2∈[0.2,0.8]。其它默认仿真参数如表1所示。

表1 仿真参数

将PDPA算法分别与经典PF算法，ML(Maximum Likelihood)算法进行对比分析。误差定义为估计位置与真实位置的均方误差，实验结果均为100次实验的均值。

4.2 跟踪效果分析

3种算法跟踪效果如图1所示，理想轨迹为椭圆形，右下角处受噪声影响轨迹发生突变，PF算法在轨迹突变处跟踪误差加大，而PDPA算法表现出较好的跟踪能力，证明其克服了PF算法在先验分布与似然分布差别较大时产生的退化现象，同时，PDPA算法克服了ML算法跟踪轨迹跳变、不稳定的问题。

4.3 环境适应能力分析

3种算法随运动噪声均值变化效果如图2所示，随着运动噪声的加大，真实轨迹与理想轨迹偏差加大，致使先验分布与似然函数交集变小，造成PF算法出现退化现象；ML算法最大误差较大，定位性能变化严重。PDPA算法在均值误差、最大误差方面均表现出良好性能。

图1 跟踪效果图

从图3可以看出，随着观测噪声的增加，ML算法误差显著增加，PDPA算法误差缓慢增加，在观察噪声方差小于60时PDPA性能优于PF算法，表明PDPA算法对观测噪声具有较好的适应能力。

参考节点间距的变化造成目标可获得的有效观测信息量发生变化，从而影响跟踪精度。图4显示出ML算法性能随间距变化较剧烈，而PDPA算法与PF算法对间距变化不是很敏感，表现出较好的密度适应性。

4.4 性能分析

PDPA算法与PF算法、ML算法性能对比如表2所示，总体来说PDPA算法适合在运动噪声与观察噪声均较大、参考节点分布不均匀的条件下工作，且算法跟踪效果波动较小。

表2 算法性能比较

3.3节中3种拟合方法性能对比如表3所示。通常情况下，在WSN应用中核系数最大的几个核函数基本上代表了后验分布的特征，基于核系数选择的方法即可满足性能要求。

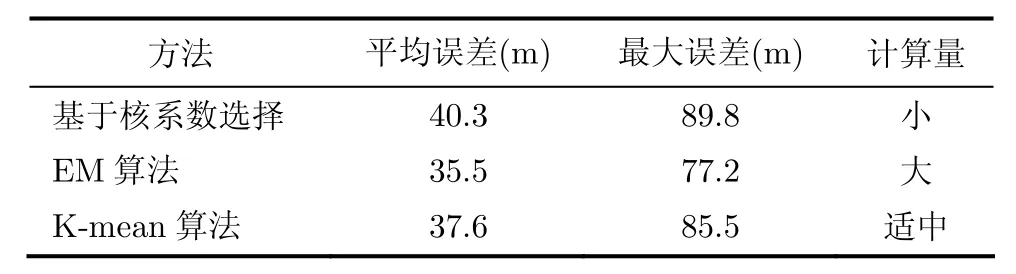
表3 拟合方法性能比较

用于表征概率分布的GMM函数核个数通常根据具体的应用环境采用实验的方法来确定，Ding在文献[11]中介绍了AIC与BIC两种核个数确定准则，亦可采用这些准则确定核个数。核个数过少会造成有用信息的丢失，同时，过多的核个数也会使一些虚假信息得到传播，GMM核个数要与噪声的多峰值特征相匹配。

5 结束语

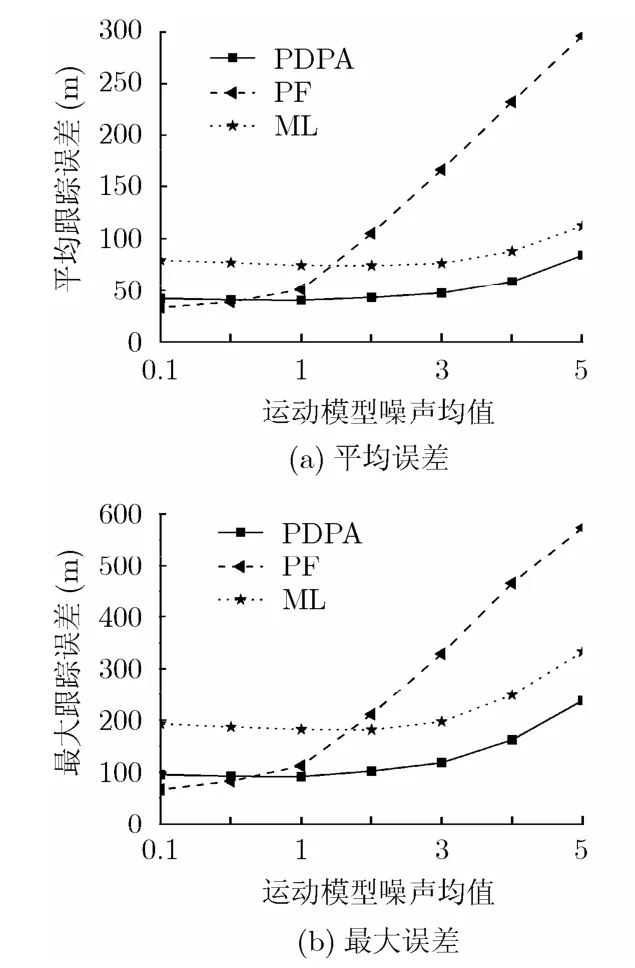
图2 误差随运动噪声均值变化

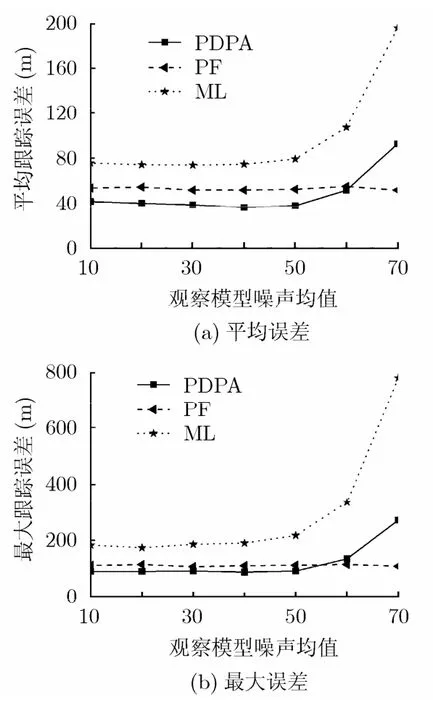
图3 误差随观测噪声均值变化

图4 误差随参考节点间距离变化

PDPA算法本质上是一种基于GMM模型表征的连续函数实现贝叶斯估计的跟踪算法，解决了PF算法采样困难的问题，实现了大噪声、非线性、非高斯环境下的目标跟踪。实验结果表明，PDPA算法适用于不同参考节点密度场合，且能在运动与观测模型噪声较大的恶劣条件下工作，是一种适用于WSN的健壮跟踪算法。进一步的研究方向为PDPA算法收敛性的证明及将该算法应用到复杂参数估计等问题中。

致谢 感谢罗海勇博士和Ding Min博士在相关算法方面的探讨。

[1] Doucet A, Godsill S, and Andrieu C. On sequential Monte Carlo sampling methods for Bayesian filtering[J]. Statistics and Computing, 2000, 10(3): 197-208.

[2] Merwe R, Doucet A, and Freitas N, et al.. The unscented particle filter[C]. 14th Annual Neural Information Processing Systems Conference, Denver, Colorado, USA, Nov.27-Dec.2,2000: 584-590.

[3] Rui Yong and Chen Yun-qiang. Better proposal distributions:object tracking using unscented particle filter[C]. Proceeding of the Conference on Computer Vision and Pattern Recognition, Hawaii, USA, Dec.9-14, 2001: 786-793.

[4] Cheng Qi and Bondon P. A new unscented particle filter[C].International Conference on Acoustics, Speech and Signal Processing, Las Vegas, Nevada, USA, March 30-April 4, 2008:3417-3420.

[5] Kotecha J H and Djuric P M. Gaussian sum particle filtering[J]. IEEE Transactions on Signal Processing, 2003,51(10): 2602-2612.

[6] Kotecha J H and Djuric P M. Gaussian particle filtering[J].IEEE Transactions on Signal Processing, 2003, 51(10):2592-2601.

[7] Luo Hai-yong, Li Jin-tao, and Zhao Fang, et al.. Mobile target localization based on mean shift in wireless sensor networks[C]. Third International Conference on Pervasive Computing and Applications, Alexandria, Egypt, October 6-8, 2008: 248-253.

[8] Baggio A and Langendoen K. Monte Carlo localization for mobile wireless sensor networks[J]. Ad hoc Networks, 2008,6(5): 718-733.

[9] Han Bohyung, Zhu Ying, and Comaniciu D, et al.. Visual tracking by continuous density propagation in sequential Bayesian filtering framework[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(5):919-930.

[10] Sheng Xiao-hong, Hu Yu-hen, and Ramanathan P.Distributed particle filter with GMM approximation for multiple targets localization and tracking in wireless sensor network[C]. Fourth International Symposium on Information Processing in Sensor Networks, Los Angeles, California, USA,April 25-27, 2005: 181-188.

[11] Ding Min and Cheng Xiu-zhen. Fault tolerant target tracking in sensor networks[C]. Proceedings of the 10th ACM International Symposium on Mobile Ad hoc Networking and Computing, New Orleans, LA, USA, May 18-21, 2009:125-134.

[12] Yuan Xiang-hui, Han Chong-zhao, and Duan Zhan-sheng, et al.. Comparison and choice of models in tracking target with coordinated turn motion[C]. IEEE 8th International Conference on Information Fusion, Philadelphia, PA, USA,July 25-28, 2005, 2: 1497-1502.