不同PKG环境下可证安全的基于身份AKA协议

夏 松 权建校 韩文报

①(解放军信息工程大学信息工程学院 郑州 450002)②(江南计算技术研究所 无锡 214083)③(解放军电子工程学院 合肥 230037)

1 引言

Shamir[1]于1984年提出了基于身份密码系统(Identity-Based Cryptograph, IBC)的概念。在IBC中，用户的唯一身份标识被用作用户公钥，有一个称作PKG(Private Key Generator)的可信中心负责给每个用户分发与其身份对应的私钥。自2001年Boneh和Franklin[2]使用双线性对技术提出了第一个安全且实用的基于身份加密机制(Identity- Based Encryption, IBE)以来，大量使用双线性对的基于身份密码机制被提出。当前，绝大部分基于身份认证密钥协商(Authenticated Key Agreement, AKA)协议都要求参与协议的用户是在同一个PKG环境下。在实际中，一个部门或区域下的用户由同一个PKG为其分发私钥，而不同部门或区域间的用户也会有安全通信的需求，这就要求在不同PKG环境下的用户也能够协商达成一个共享的会话密钥。Chen和Kulda[3]在2003年第一次提出了在不同PKG环境下的用户之间实现AKA协议的思想。2005年McCullagh和Barreto[4]提出一个可以在不同PKG环境下的用户之间实现的AKA协议 (简记为MB协议)，但随后被指出无法抵抗KCI(Key Compromise Impersonate)攻击。

在以往的协议安全性证明中，为了在模拟游戏中实现敌手的判定性询问，设计的协议多是基于gapDH(Diffie-Hellman)困难性问题，然而gap DH困难性假设是一个比较强的假设。在2008年的欧密会上，Cash，Kiltz和Shoup[5]提出了twin DH问题，它能够在容许对问题进行判定性询问的情况下保持问题的困难性，而这个性质并不是一般的DH问题所具备的。其中实现对twin DH问题进行判定性询问的核心方法是“trapdoor test”技术，它能够在不知道相关离散对数的情况下实现对twin DH问题的判定性询问。近期黄海和曹珍富[6]结合twin DH问题提出了一个新的基于身份AKA协议，而且利用“trapdoor test”技术实现了在eCK(extended Canetti-Krawczyk)模型[7−9]下的严格安全性证明。受这些已有结论的启发，结合twin DH问题本文提出了一个新的在不同PKG环境下的用户之间实现的AKA协议，并且利用trapdoor test技术在模拟游戏中实现判定性询问，在目前最强的eCK模型中将新协议的安全性规约到标准的CDH(Computational DH)和BDH(Bilinear DH) 假设。

本文第2节介绍背景知识；第3节描述新协议；第4节在eCK模型下对新协议进行安全性证明；第5节进行性能评估；最后总结全文。

2 预备知识

2.1 相关密码组件及关键技术

双线性映射 如果G是阶为q的加法循环群，GT为同阶的乘法循环群，P是G的任一生成元，双线性映射: G×G→GT满足以下性质：

(3)可计算性：对∀Q, R∈G，存在一个有效的多项式时间算法来计算(Q, R)。

困难性假设 CDH假设：对未知的x, y∈Zq，给定X=xP和Y=yP，计算Z=xyP是困难的；BDH假设：对未知的x, y, z∈Zq，给定X=xP，Y=yP和W=wP，计算Z=e(P, P)wxy是困难的。

定理1(“trapdoor test”技术[5,6]) 设e: G×G→GT是一个双线性对，其中G，GT是阶为大素数q的循环群，P是G的一个生成元。假设W1，r，s是相互独立的随机变量，其中W1∈G，r，s是Zq上均匀分布的，定义W2=sP−rW1。假设X，Y是取值于G的随机变量，Z1，Z2是取值于GT的随机变量，并且Z1，Z2都是W1，W2的函数，则有：

(1)W2在G上是均匀分布的；

(2)W1，W2相互独立；

(3)如果W1=w1P, W2=w2P ，那么

式(1)不成立时，式(2)成立的概率至多是1/q，且式

(2)成立时则式(1)一定成立。

2.2 安全模型

本节简要描述适用于基于身份AKA协议的扩展后的eCK模型，具体介绍参见文献[7-9]。

协议参与者 协议的每一个参与者被视为一个概率多项式时间的图灵机，每个参与者有一个身份IDi，并且每个参与者可以并行地执行多个会话实例。记参与者IDi与参与者IDj的第s个实例为。

通过一个在模拟者S和攻击者M之间的游戏来定义AKA协议的安全性，攻击者M是一个概率多项式时间的图灵机，并且控制整个通信网络。通过给予敌手oracle询问来模拟敌手的攻击能力：

Long-term key reveal(IDi)：M得到协议参与者IDi的长期密钥；

PKG Long-term key reveal(PKGi)：M得到PKGi的主密钥；

Establish Party(IDi)：M可以代表IDi通过对应的PKG注册一个合法用户，M得到IDi的长期密钥并且完全控制IDi；

最后，M输出一个对b的判断(记为b')。若b'＝b，那么称M赢得了此游戏。记Σ为一个AKA协议，定义M攻破AKA协议Σ的优势为=，其中k为安全参数。

(a)Long-term Key Reveal(IDi) 和 Ephemeral-term Key Reveal()；

(b)Long-term Key Reveal(IDi) 和 Ephemeral-term Key Reveal()。

(a)Long-term Key Reveal(IDi) 和 Ephemeral-term Key Reveal()；

(b)Long-term Key Reveal(IDi)。

定义3 如果协议Σ满足以下条件，称协议Σ是安全的AKA协议：

3 不同PKG环境下的基于身份AKA协议

本节给出一种新的在不同PKG环境下的基于身份AKA协议，新协议由系统建立、私钥生成和密钥协商3个阶段组成。

系统建立：G是阶为大素数q的加法循环群，GT为同阶的乘法循环群，P为G的一个生成元，G*为G中的非用户身份元素集，k为系统的安全参数，λ为临时密钥的长度，eˆ: G×G→GT为双线性映射。Hash函数H1, H2:{0,1}*→G*，H3:{0,1}λ×G0→，H:{0,1}*→{0,1}k。随机选取u，v∈Zq，令U=uP，V=vP。 设置u，v分别为 PKG1，PKG2的主密钥，U，V分别为 PKG1， PKG2的公钥。分别以C1，C2表示PKG1，PKG2的用户集。

私钥生成：对用户A∈C1，对应的IDA∈{0,1}*，PKG1计算 QA1=H1(IDA)，QA2=H2(IDA) 及相应的私钥dA1=uQA1，dA2=uQA2给A。对用户B∈C2，对应的IDB∈{0,1}*，PKG2计算 QB1=H1(IDB)，QB2=H2(IDB)及相应的私钥dB1=vQB1，dB2=vQB2给B。分别记Apri=dA1，Bpri=dB1。

密钥协商：用户A和B分别随机选取一个临时密钥，分别记为x，y∈R{0,1}λ，然后分别计算x=H3(, Apri)，y=H3(, Bpri)及相应的临时公钥X=xP，Y=yP，随即分别销毁x，y。然后，A和B相互交换协议数据X和Y，记sid=(X, Y,A, B)。消息传递完成后，A和B分别执行如下步骤：

4 安全性证明

本节在第2.2节定义的安全模型下证明新协议的安全性。

定理2 若Hash函数被模型化为随机预言机，且CDH假设及BDH假设成立，则新协议是一个安全的AKA协议。

证明 假设k是系统的安全参数，攻击者M激活至多n(k)个诚实用户，每个用户至多激活s(k)个并行会话。假设M在第2.2节的模型中能以不可忽略的优势得到测试会话的会话密钥，由于H是随机预言机，因此在M进行test询问后，只有下面两种情况区分会话密钥和随机数。

情况1 伪造攻击：在攻击的某一时刻，M向H询问了(Z1, Z2, Z3,X, Y, A, B)，因H是随机预言机，所以此时M自己计算了Z1, Z2, Z3。

情况2 密钥复制攻击：M强迫一个非匹配会话与测试会话具有相同的会话密钥。这样M可以通过简单的请求这个非匹配会话，来得到测试会话密钥。

对于情况2，因为H为随机预言机，所以不同的会话中H的输入不可能相同，也就不会得到相同的会话密钥。因此M通过密钥复制攻击成功的概率可忽略不计。下面主要分析情况1，根据新鲜会话的定义，从两种情况来考虑：情况1.1不存在测试会话的匹配会话；情况1.2存在测试会话的匹配会话。

4.1 不存在测试会话的匹配会话

情况1.1可分为下面两种情况：

情况1.1.1：在某一时刻，M得到A的长期密钥。不失一般性，我们假设A∈C1。

如果存在M以不可忽略的优势ε(k)赢得游戏，那么我们可以利用M构造一个算法攻击BDH假设。即给模拟者S一个BDH实例：V=vP, Z=zP,W=wP，要求S利用M计算BDH(V, Z, W)=e(P, P)vzw。S随机选择U(U∈G)作为PKG1的公钥，令V作为PKG2的公钥。S至少以1/n(k)2的概率猜测测试会话是在A和B(B∈C2)之间进行，又以至少1/s(k)的概率猜测M会选择A的会话s作为测试会话。S随机选取s, r∈Zq，设置B的公钥为QB1=W1=W ，QB2=W2=sP−rW ，为其它n(k)−1个用户(包括A)随机分配公/私钥对。如果拥有M激活用户的长期密钥，S根据协议流程执行。因S不知道B的长期密钥，所以当M向S发出关于B的询问请求时，S的模拟行为如下：

H1(IDi)：S记录一个最初记录为空的列表，记录的格式为((IDi,li1,Qi1)，

(1)若IDi在列表中，S回答相应的Qi1；

H2(IDi)：S记录一个最初记录为空的列表，记录的格式为((IDi,li1,Qi1)，

(1)若IDi在列表中，S回答相应的Qi2；

(2)若IDi不在列表中，如果IDi=B，S随机选择r, s∈Zq，令QB1=W1=W,QB2=W2=sP −rW，添加(B,null,QB2)到，同时添加(B,null,Q)到；否则，S随机选择l,l∈Z，计算

B1i1i2qQi1=li1P, Qi2=li2P ，添加(IDi,li2,Qi2)到，并且添加(IDi,li1,Qi1)到。

Establish Party(IDi)：S代替M注册一个用户IDi，即S向H1, H2询问IDi。若IDi∈C1，返回dIDi1=li1U, dIDi2=li2U 给敌手，否则IDi∈C2，返回dIDi1=li1V, dIDi2=li2V 给敌手。

Long-term Key Reveal(IDi)：如果IDi=B，S退出游戏(事件E1)；否则返回相应的私钥。

(1)如果IDi=A并且是测试会话，那么S返回Z给M；

除臭规模总风量Q为13 000 m3/h，共计2套处理系统，其中，一期设计风量9 000 m3/h，二期设计风量4 000 m3/h，除臭工艺采用生物土壤滤池除臭技术。首先将O池中的恶臭气体密封加盖，防止恶臭气体外溢，采用不锈钢收集风管进行收集，通过引风机将恶臭气体引至生物土壤滤池进行处理，处理后的气体无组织达标排放。

(2)如果IDi=B，设IDj=C, m=X ，S随机选择y∈Zq，把Y=yP返还给M，S在Hlist中查找

若式(3)成立，则由定理1有

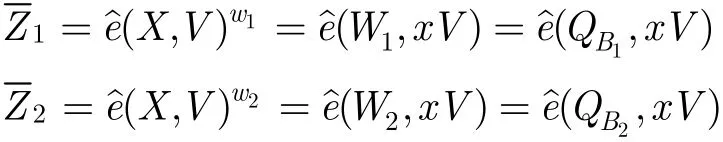
S查看

如果(X, Y, C, B)在列表Hlist中，S计算询问中的方法相同，S根据定理1验证是否正确生成，并通过计算来验证是否正确生成。若经验证都是正确生成的，那么S返回列表Llist中的对应值SK并添加到列表listH中。否则，S随机随机选择作为返回值，并添加到列表listH中。

否则，S随机随机选择{0,1}kh∈作为返回值，并添加到列表listH中。

在这种攻击类型中，若S未退出游戏，则M以不可忽略的概率攻击成功并向H询问过关于测试会话的7元组，其中。为了解决BDH难题，S随机选择Hlist中的一个记录IDi,IDj,h)，对于进行如下计算：

这样S成功解决了BDH难题，与BDH假设矛盾。

令E5代表M赢得游戏，即有。若S猜中测试会话s，且情况1.1.1发生，则事件E1～E4都不发生，故p(k)/(s(k) n(k)2)，其中p(k)是情况1.1.1发生的概11率。令E7代表S获得正确的和，则有Pr[E7]≥1/t(k)，其中t(k)为攻击者询问H的次数。那么S成功解决BDH问题的优势为

情况1.1.2：M始终没有得到A的长期密钥。

如果存在M以不可忽略的优势ε(k)赢得游戏，那么我们可以利用M构造一个算法攻击BDH假设。给模拟者S一个BDH实例：U=uP, Z=zP,W=wP，要求S利用M计算BDH(U, Z, W)=e(P, P)uzw。S取U作为PKG1的公钥，随机选择V (V∈G)作为PKG2的公钥。S至少以1/n(k)2的概率猜测测试会话是在A (A∈C1)和B(B∈C2)之间进行，又以至少1/s(k)的概率猜测M会选择A的会话sˆ作为测试会话。S随机选取s, r∈Zq，设置A的公钥为QA1=W1=W ，QA2=W2=sP−rW ，随机选取QB1，QB2作为B的公钥，为其它n(k)−2个用户随机分配公/私钥对。下面描述S区别于情况1.1.1的模拟行为：

H1(IDi) ：如果IDi=A，S随机选择r, s∈Zq，令QA1=W1=W,QA2=W2=sP−rW ，添加(A,null,QA1)到，相应添加(A,null,QA2)到；如果IDi=B，S随机选择QB1，QB2作为B的公钥，添加(B,null,QB1)到，同时添加(B,null,QB2)到。

H2(IDi)：模拟同H1(IDi)。

在这种攻击类型中，若S未退出游戏，则M以不可忽略的概率攻击成功并向H询问过关于测试会话的7元组，其中为了解决BDH难题，S随机选择Hlist中的一个记录(,,,X, Y,IDi,IDj,h)，对于,进行如下计算：其中Y是由M选择的，X是S选择的，因此S知道x。S随机的选择，然后计算：

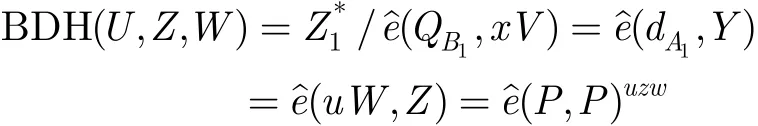
这样S成功解决了BDH难题，与BDH假设矛盾。

类似于情况1.1.1中的分析，可得S成功解决BDH问题的优势为⋅t(k)]，其中p2(k)是情况1.1.2发生的概率，t(k)为攻击者询问H的次数。

4.2 存在测试会话的匹配会话

根据新鲜会话的定义，情况1.2可分为下面4种情况：

情况1.2.1：攻击者得到A，B的长期密钥。

如果存在攻击者M以不可忽略的优势ε(k)赢得游戏，那么我们可以利用M构造一个算法攻击CDH假设。给模拟者S一个CDH实例：X=xP,Y=yP(X, Y∈G)，要求S利用M计算CDH(X, Y)=xyP 。S至少以2/s(k)2的概率选中两个会话，其中一个为测试会话，另一个为对应的匹配会话。设置测试会话发起者A的临时密钥为X，响应者B的临时密钥为Y。如果M攻击成功，那么攻击者肯定向H询问过关于测试会话的7元组所以S输出CDH(X, Y)=。这样S就解决了CDH难题。这里S成功解决CDH问题的优势为，其中p3(k)是情况1.2.1发生的概率，t(k)为攻击者询问H的次数。

情况1.2.2：攻击者得到A，B的临时密钥。

情况1.2.3：攻击者得到A的长期密钥，B的临时密钥。

情况1.2.4：攻击者得到A的临时密钥，B的长期密钥。

对情况1.2.3和情况1.2.4这两种情况，S的模拟行为与情况1.1.1的情况类似，这里不再赘述。

综合上述分析，如果存在攻击者M以不可忽略的优势ε(k)赢得游戏，在情况1.1.1，情况1.1.2，情况1.2.3和情况1.2.4这4种情况中，模拟者S解决BDH难题的优势为其中p4(k)，p5(k)分别为情况1.2.3，情况1.2.4发生的概率。在情况1.2.1中，S解决CDH难题的优势为

因此，若攻击者M在上述任一情况下能以不可忽略的优势对协议攻击成功，那么我们就可以利用M以不可忽略的优势来解决BDH或CDH难题。这与协议所基于的安全假设相矛盾。所以新协议满足定义3中的条件(2)。若协议参与双方的对话是匹配的，这意味着他们正确地收到了对方发来的协议消息，那么他们能够计算得到相同的会话密钥，且该密钥均匀分布于会话密钥空间，因此定义3中的条件(1)也是满足的。所以新协议是一个安全的AKA协议。

5 性能评估

Chow和Choo利用挑战-响应签名技术提出一种新的基于身份AKA协议[10]，用CC-1协议和CC-2协议分别表示文献[10]中的第1个和第2个协议。考虑到MB协议[4]，CC-1协议[10]和CC-2协议[10]的高效性能，文献[6]中的协议在安全方面的优势，本节将新协议与这4个协议进行安全性能、使用效率和适用范围方面的比较，见表1。由于各协议都满足基本的安全属性，在此仅考虑完善前向安全(p-FS)，PKG前向安全(PKG-FS)，抗密钥泄露伪装攻击(KCI)和抗临时密钥泄露攻击(EKCI)。“√”表示满足属性，“×”表示不满足属性。在比较使用效率时，用P表示双线性对运算，E表示G中的指数运算，T表示GT中的指数运算，统计内容为协议成功运行一次的单方运算消耗。在比较协议适用范围时，“√”表示该协议能被应用在不同PKG环境中，“×”表示不能。

6 结束语

本文针对不同PKG环境提出了一种全新的基于身份AKA协议。利用Cash等人在2008年欧密会上提出的trapdoor test技术在eCK模型下给出了严格的形式化安全证明。通过比较可见，新协议同时具有安全性和适用性上的优势。如何进一步提高协议的执行效率是我们下一步要研究的工作。

表1 基于身份AKA协议的性能比较

[1] Shamir A. Identity based cryptosystems and signature schemes[C]. CRYPTO’84, Santa Barbara, California, USA,August 19-22, 1984, LNCS 0196: 47-53.

[2] Boneh D and Franklin M. Identity based encryption from the Weil pairing [C]. CRYPTO’01, Santa Barbara, California,USA, August 19-23, 2001, LNCS 2139: 213-229.

[3] Chen L and Kudla C. Identity based authenticated key agreement protocols from pairing[C]. 16th IEEE Security Foundations Workshop, Los Alamitos, CA, USA, June 30-July 2, 2003: 219-233.

[4] McCullagh N and Barreto P S L M. A new two-party identity-based authenticated key agreement[C]. CT-RSA 2005, San Francisco, CA, USA, February 14-18, 2005, LNCS 3376: 262-274.

[5] Cash D, Kiltz E, and Shoup V. The twin diffie-hellman problem and applications[C]. EUROCRYPT2008, Istanbul,Turkey, April 13-17, 2008, LNCS 4965: 127-145.

[6] Huang Hai and Cao Zhen-fu. An ID-based authenticated key exchange protocol based on bilinear Diffie-Hellman problem[C]. ASIACCS 2009, Sydney, Australia, March 10-12,2009: 363-368.

[7] Canetti R and Krawczyk H. Analysis of key-exchange protocols and their use for building secure channels[C].EUROCRYPT 2001, Innsbruck, Austria, May 6-10, 2001,LNCS 2045: 453-474.

[8] LaMacchia B, Lauter K, and Mityagin A. Stronger security of authenticated key exchange[C]. ProvSec 2007, Wollongong,Australia, October 31 - November 2, 2007, LNCS 4784: 1-16.

[9] Ustaoglu B. Obtaining a secure and effcient key agreement protocol from (H)MQV and NAXOS[J]. Designs, Codes and Cryptography, 2008, 46(3): 329-342.

[10] Chow S S M and Choo K R. Strongly-secure identity-based key agreement and anonymous extension. Information Security, Volume 4779/2007, Springer Berlin Heidelberg,203-220, 2007. Cryptology ePrint Archive, Report 2007/018.Full version of this paper (2007).