Schrödinger算子的Riesz平均不等式
赵 琳, 贾 高
(上海理工大学理学院,上海 20093)
1 问题的提出
Schrödinger方程是在1926年提出的,它是量子力学的基本方程,它的提出使得量子力学许多核心的问题得以解决.因此,在数学领域对Schrödinger算子的研究也随之增加,对其谱理论的研究便是研究热点之一.
一般来说,瞬间热核膨胀中,正常高频光谱密度在膨胀的前期和后期并不完全一致,但是,Riesz平均通过对低频密度光谱求平均的方法,消除了光谱密度在高频区的震荡,使得光谱密度的各个阶段在Riesz平均意义下是严格一致的.因此,对 Riesz平均的进一步研究,无论是对于数学理论还是应用领域都有着十分重要的意义.
文章主要讨论定义在有界区域Ω⊂Rd(d≥1)上的Schrödinger算子-Δ+V(x)的离散谱,利用有关特征值估计的迹公式,采用一种新的方法证明了特征值Riesz平均的微分不等式和差分不等式,进而得到有关Riesz平均的单调性.
2 预备知识
如果λj,uj满足方程-Δuj+V(x)uj=λjuj(j =1,2,3,…),便称uj为Schrödinger算子-Δ+V (x)的特征函数,λj为Schrödinger算子-Δ+V(x)对应于特征函数uj的特征值.根据微分方程理论,在一定的条件下,Schrödinger算子的特征值是存在的,而且是离散的.
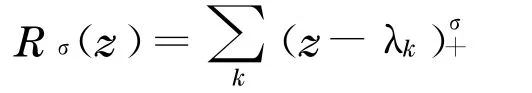
注:根据定义有

引理1[1]设为Schrödinger算子-Δ+ V(x)对应于特征值的 L2-正规化特征函数,记2,…,d.那么对于每一个固定的α,成立

引理2[2](Hadamard不等式)设φ是区间[a, b]上的凸函数,则对于a≤x1<x2≤b,有
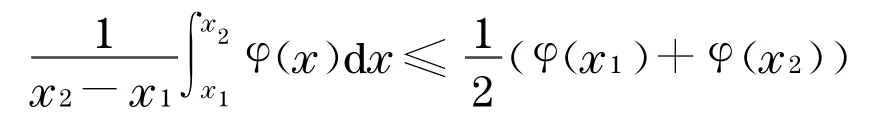
仅当φ为线性函数时等号成立.
引理3 对于0<x<y,σ≥0,则成立

式中Cσ是一个与σ有关的常数:


的上确界.下面分两种情况讨论:
a.2<σ<∞或0≤σ<1.
令f(t)=tσ-1,t∈[1,a],∀a>1.因为当2<σ<∞或0≤σ<1时,f(t)在t∈[1,a]上为凸函数,所以对∀1<y≤a利用引理2得
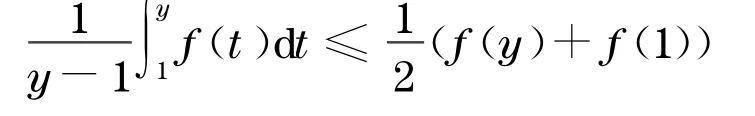
即
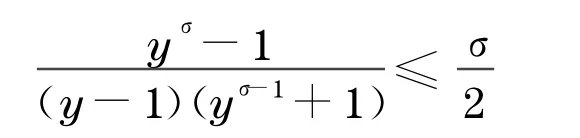
b.1≤σ≤2.因为

引理4[3]设 d≥3,对于 Schrödinger算子-Δ+V(x)中的V(x),若是有限的,则存在仅依赖于维数d的常数Kd,使得
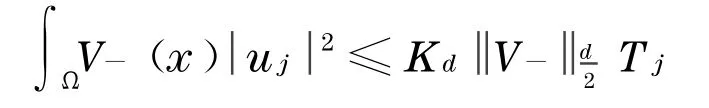
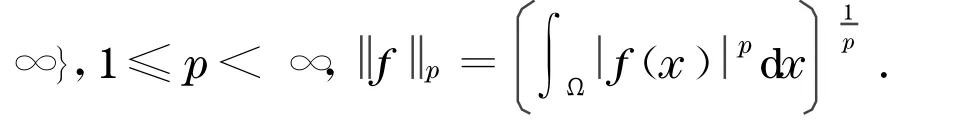
由文献[1]知:对于Schrödinger算子,若V(x)满足一定的假设条件,那么能够被λj乘以一个常数进行约束,而且因V(x)的假设条件不同,这种约束存在有很多种情况,所以,为了后面的证明可作以下假设:
假设∑ 存在0<ρ<∞,使得Tj<ρ λj成立.
事实上,假设∑包含了以下3种特殊情况:
a[4].若V(x)≥0,则ρ=1;
b[1].对于则
下面证明假设∑中c的情况.
定理1 设λj为Schrödinger算子-Δ+V(x)的第j个特征值,若则有

证明 因为{um}为完备正交系,再利用引理4得

所以结论成立.
3 主要结论
下面叙述文中的主要结论,此结论包括:Riesz平均关于σ的差分不等式和关于z的微分不等式两部分.
定理2 在满足假设∑的条件下,若2≤σ<∞, z≥0,则成立


证明 记

由引理3可得
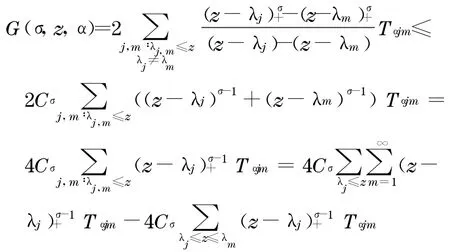
由引理1可得
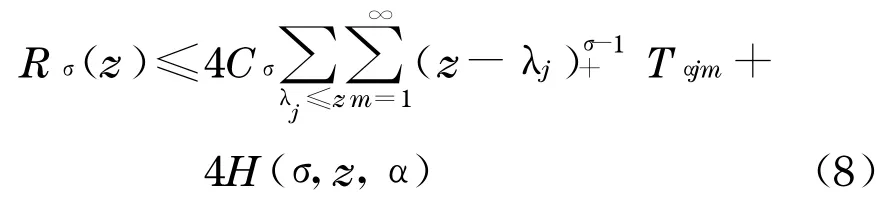
式中

在式(8)中对α=1,2,…,d求算术平均,并由假设∑可得

利用式(1),则从式(9)得

即
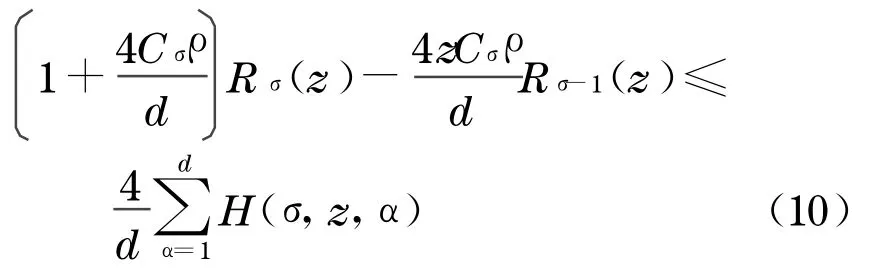
下面分3种情况讨论:
情况1 1≤σ≤2.此时Cσ=1,所以
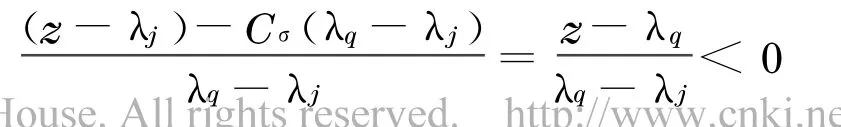

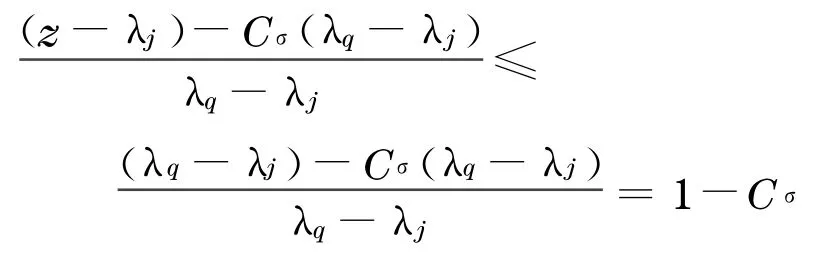
于是
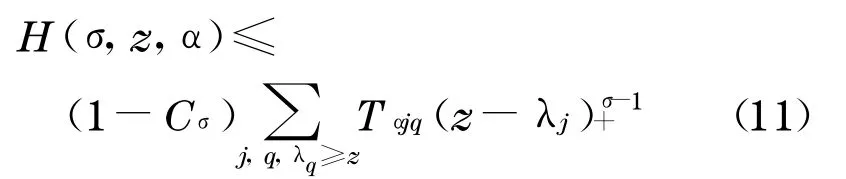
又因为1-Cσ>0,所以在式(11)中对所有的q和α求和,得到
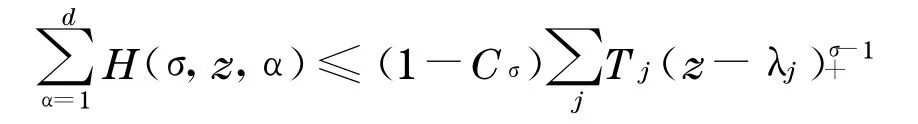
利用假设∑和式(1),可得


另一方面,

同理
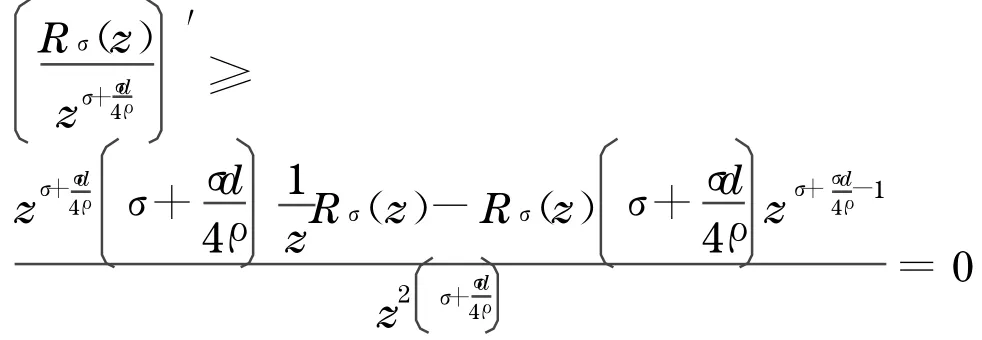
[1] HARRELE M,STUBBE J.On trace identities and universal eigenvalue estimate for some partial differential operators[J].Trans.Amer.Math.Soc.,1997,349: 1 797-1 809.
[2] 匡继昌.常用不等式[M].济南:山东科学技术出版社,2003.
[3] ALLEGRETOOW.Lower bounds on the number of points in the lower spectrum of elliptic operators[J]. Can.J.Math.,1979,31:419-426.
[4] HARREL E M,HERMI L.On riesz means of eigenvalues [J/OL].[2008-11-01].http:∥arxiv.org/ps_cache/ arxiv/pdf/0712.4088vl.pdf
[5] AIZENMAN M,LIEB E H.On semi-classical bounds for eigenvalues of Schrödinger operators[J].Phys.Lett., 1978,66:427-429.
[6] EASTHAM M S P,KALF H.Schrödinger-Type operators with continuous spectra[M].Boston:Pitman Advanced Pub,1982.
[7] PETER L I,YAU Shingtang.On the Schrödinger equation and eigenvalue problem[J].Commun.Math.Phys., 1983,88:309-318.
[8] HARREL E M,HERMI L.Differential inequalities for Riesz means and Weyl-type bounds for eigenvalues[J]. Journal of Functional Analysis,2008,254:3 173-3 191.
