实现分数阶傅里叶变换的光学系统及其应用

孙桂林，江炎兰

（1.海军航空工程学院系统科学与数学研究所，山东 烟台 264001；2.国防科学技术大学，长沙 410073）

0 引言

自1807年傅里叶变换问世以来，迅速在科学技术的各个领域得到了深入的研究和广泛的运用。正是由于这些研究和应用，逐渐暴露了傅里叶变换在研究某些问题及处理某些特殊数据时的局限性。

1946年，D.Gabor[1]从一个方向改进了傅里叶变换，给出了以他的名字命名的Gabor变换，最终导致小波分析的出现；而V.Namias[2]从完全不同的角度出发，在1980年给出了傅里叶变换的改进形式，也就是分数阶傅里叶变换（也称为分数傅里叶变换）。

1993年，分数阶傅里叶变换由Mondlovic[3-4]等人最先引入到光学研究中。Ozaktas 和Mendlovic[4]提出用平方折射率光波导（GRIN）实现分数阶傅里叶变换，而Lohmann[5]等人利用傅里叶变换相当于Wigner 分布函数相空间中角度为π/2的旋转的这一性质，阐释了分数阶傅里叶变换的物理意义，并提出利用非常简单的单透镜和双透镜结构实现分数阶傅里叶变换，也就是Lohmann I 和LohmannII 光学结构。

自此，由透镜分立光学元件组成的光学系统成为分数阶傅里叶变换光学实现的重要方式之一。

本文利用ABCD 定律分析了实现分数阶傅里叶变换的3个基本光学系统；归纳了分数阶傅里叶变换在光学中的应用；最后指出了分数阶傅里叶变换在光学系统中进一步的发展方向。

1 分数阶傅里叶变换的变换矩阵及光场表达式

1.1 分数阶傅里叶变换矩阵

已知谢尔维斯特定理，

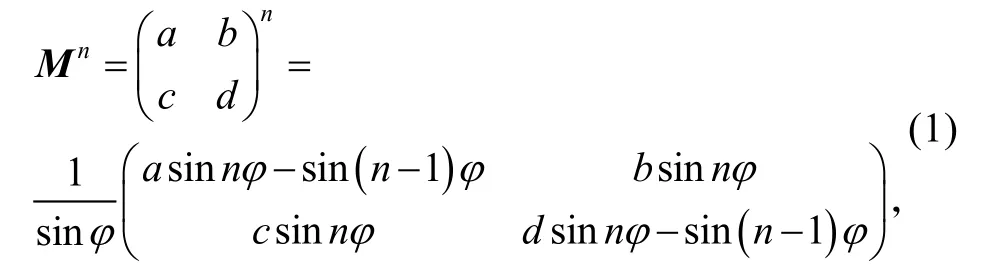
已知傅里叶变换矩阵为

设P/Q 阶傅里叶变换矩阵为

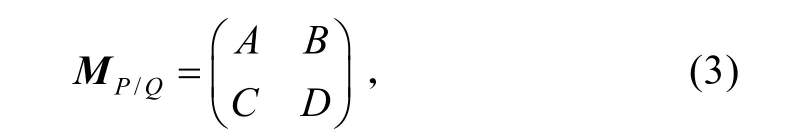
根据分数阶傅里叶变换的定义，得到

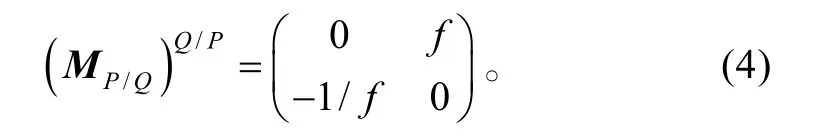
利用谢尔维斯特定理及以上各式，解得

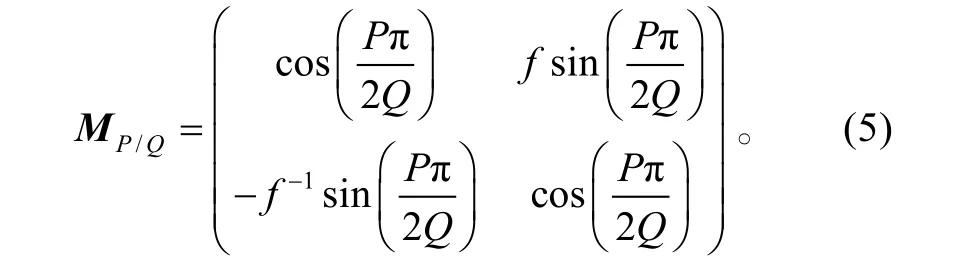
1.2 光场表达式

由柯林斯（Collins）公式，经ABCD 矩阵变换前后的光场关系为：

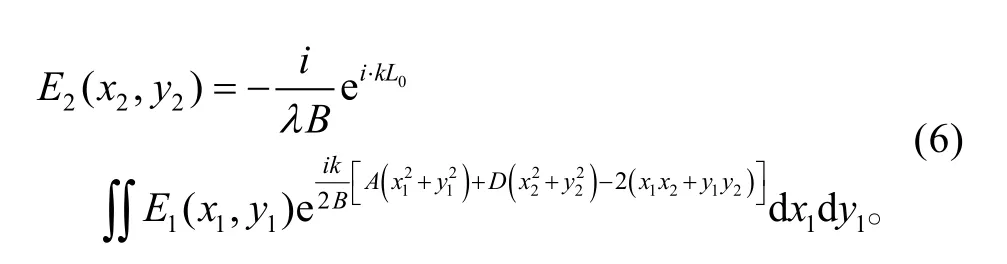
将变换矩阵式(5)代入Collins 式(6)中，可以得到P/Q 阶傅里叶变换后的光场的表达式：

式(7)即为光学上P/Q 阶分数阶傅里叶变换的积分表达式。

2 光学系统对分数阶傅里叶变换的实现

一般认为，光学上有3种方式可以实现分数阶傅里叶变换，即类透镜介质光波导、Lohmann I 和Lohmann II 光学结构。下面利用传输矩阵方法分别讨论这3种基本光学结构是如何实现分数阶傅里叶变换的。

2.1 类透镜介质实现分数阶傅里叶变换

正透镜介质中的折射率与径向关系为，

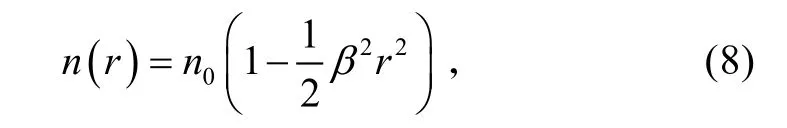
式中，β ＞0，且β＜＜1，n β、分别为折射率和参数，则传输矩阵为

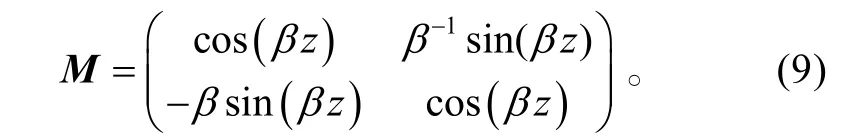
与分数阶傅里叶变换矩阵式(5)比较可知，对于正透镜介质当传输距离为时，实现阶傅里叶变换。

2.2 Lohmann I 光学系统

Lohmann I 光学系统是利用类单透镜前后焦面关系，设计P/Q 阶傅里叶变换光学系统，图1给出了该光学系统的表示。

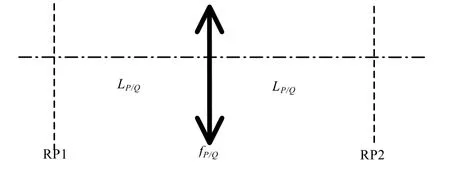
图1 Lohmann I 光学系统

此光学系统的传输矩阵为：

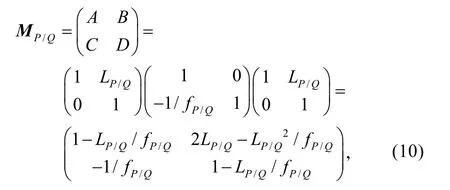
式中：

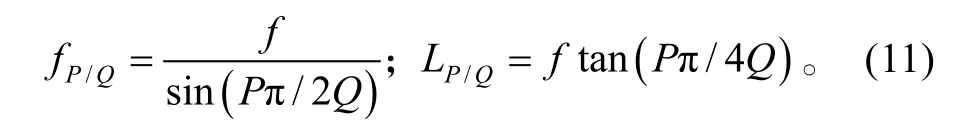
由此我们可以看到，

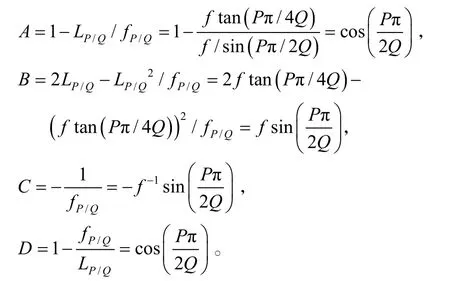
与分数阶傅里叶变换矩阵式(5)对比，我们可以看到当fP/Q、LP/Q满足式(11)条件时，Lohmann I光学系统即可实现分数阶傅里叶变换。

2.3 Lohmann II 光学系统

图2给出了利用两个完全相同的透镜和一段传输距离设计分数阶傅里叶变换系统。

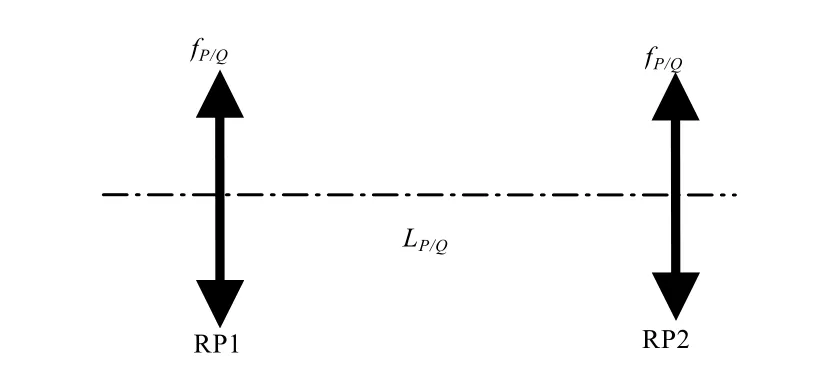
图2 Lohmann II 光学系统

此光学系统的传输矩阵为：

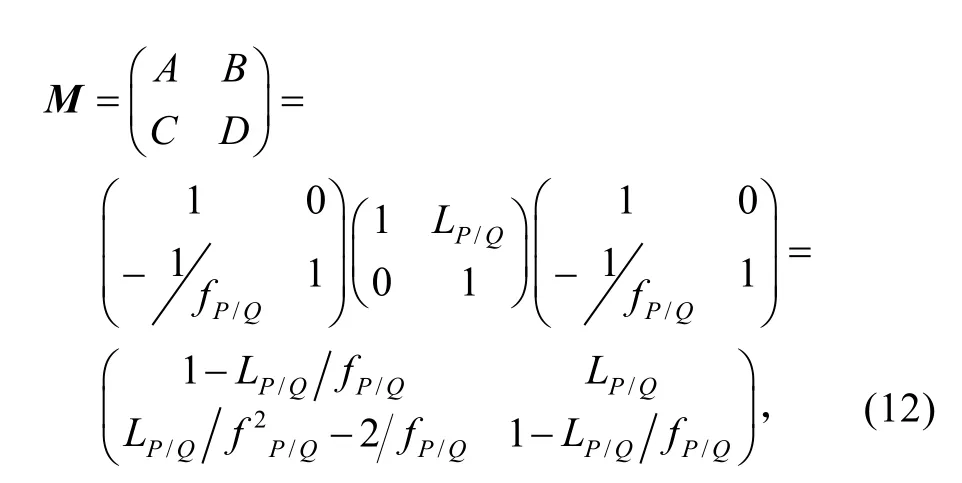
式中，

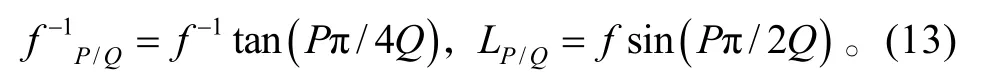
由此我们可以看到，

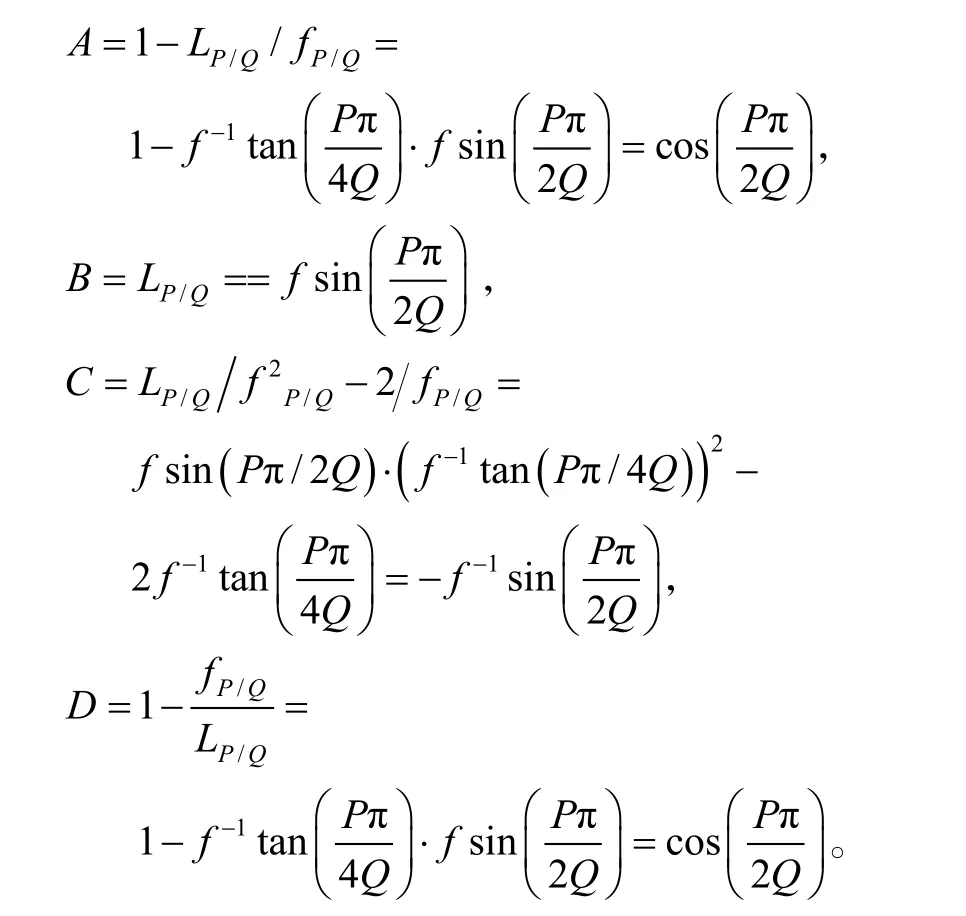
与分数阶傅里叶变换矩阵式(5)对比，我们可以看到当fP/Q、LP/Q满足式(13)条件时，Lohmann II光学系统即可实现分数阶傅里叶变换。

3 分数阶傅里叶变换在光学中的应用

分数阶傅里叶变换比傅里叶变换在处理各种问题时更加灵活。因此，自问世以来分数阶傅里叶变换在各个领域的应用研究便是一个热点。分数阶傅里叶变换是傅里叶变换的推广。因此，在傅里叶变换适用的领域分数阶傅里叶变换也同样适用，并呈现出新的特性。

3.1 分数阶傅里叶变换在图像处理中的应用

由于分数阶傅里叶变换具有傅里叶变换在图像处理中所不具有的一些重要性质，因此在图像处理中较傅里叶变换有更广泛的应用[6]。

基于分数阶傅里叶变换的图像加密和复原。目前应用傅里叶变换光学系统对图像进行加密的方法已远远不能满足现实要求。2000年，G.Unnikrishnan和刘树田[7-9]等人提出用分数阶傅里叶变换实现图像的双随机相位加密后，由于其对傅里叶变换系统保密性能的优化，使得利用分数阶傅里叶变换进行图像加密迅速成为国内外研究的热点[10-13]。1995年，Mendlovic D[14-15]等人又提出变形分数阶傅里叶变换光学实现的理论。此后不断有利用变形分数傅里叶变换进行图像加密和复原的研究出现[16-19]。由于每个自由度的加密阶数不定，加密位置、数量不定，使得加密后的图像更加安全，图像的破解更加困难。图像复原是原系统的逆过程，加密的复杂性也就增加了解密的复杂性。利用分数阶傅里叶变换进行图像加密是现在研究的热点。可以想见，由于变形分数傅里叶变换进行图像加密的优越性，必然是未来理论和技术研究的热点。

基于分数阶傅里叶变换的图像数字水印技术是将版权信息隐藏于被保护的数字信息内，因而有效的数字水印算法应具有水印信息的不可见性、抗噪音鲁棒性和较高容量。原始的数字水印算法是利用小波的双域分析能力，由此联想到分数阶傅里叶变换也是双域的，并且具有优于小波变换的全域特性。我们把水印信息隐藏在被保护信息的低频分数傅里叶谱部分的系数上，并同时将水印信息做离散分数傅里叶变换，用它的低频分量代替水印信息。这样既降低了水印嵌入的信息量，又可以增加水印信息的安全性[20-21]。

分数阶傅里叶变换全息图。分数阶傅里叶变换全息图[22]是在分数阶傅里叶变换域上用全息的方法记录下的物光波的分数阶傅里叶变换分布，由于分数阶傅里叶变换自由度的变化，因此不仅能记录物体的信息，也记录了记录系统的信息，开拓了分数阶傅里叶变换的更多应用领域。全息图的记录和再现方式的数字式实现是目前全息术的一个重要方向。

3.2 基于分数阶傅里叶变换的联合相关器

在模式识别中，基于分数阶傅里叶变换联合相关器较传统的基于傅里叶变换的联合相关器有较大改善[23-25]，尤其是在畸变物体或多个物体识别中更是显示出很大的优越性[26-28]。近年来也出现了变形分数阶傅里叶变换相关器的一些研究[29]。分数相关器是通过对畸变信号的补偿来实现较好的相关输出的，而变形分数傅里叶变换相关器是通过两个自由度的畸变补偿实现相关输出。文献[29]指出分数阶傅里叶变换相关器较传统相关器有较大改善，但是实际应用中由于受到仪器精度的限制，还没有得到广泛应用。

3.3 利用分数阶傅里叶变换分析光学谐振腔

利用光学传输矩阵和含透镜的光腔的分数阶傅里叶变换的性质分析谐振腔的稳定性在方法上是比较方便的，并且在物理图像上是比较直观的[30-31]。

4 结论

本文对分数阶傅里叶变换的发展历程进行了简单回顾，应用ABCD 矩阵方法分析了实现分数阶傅里叶变换的3个基本光学系统，并就分数阶傅里叶变换在光学中的几种应用进行了归纳总结。

自分数阶傅里叶变换出现以来人们就一直对它不断进行研究。变形分数傅里叶变换相较分数阶傅里叶变换又有许多特别的优势，但是变形分数傅里叶变换的光学实现对仪器精度要求比较高，计算量比较大。可以想见，由于变形分数傅里叶变换的特殊性质，未来对分数阶傅里叶变换的研究必然倾向于对变形分数傅里叶变换的研究。而且伴随着理论和技术的提高，必然会为变形分数傅里叶变换提供更广阔的发展空间。

[1]GABOR D.Theory of communication[J].Inst.Elect.Eng,1946,93(3):429-457.

[2]NAMIAS V.The fractional order Fourier transform and its application to quantum mechanics[J].Inst.Maths Appl,1890,25:241-265.

[3]MENDLOVIC D,OZAKTAS H M.Fractional Fourier transforms and their optical implementation(I)[J].Opt.Sco.AM.A.,1993,10(10):1875-1881.

[4]OZAKTAS H M,MENDLOVIC D.Fractional Fourier transforms and their optical implementation(II)[J].Opt.Sco.AM.A.,1993,10(10):2522-2531.

[5]LOHMANN A W.Image rotation,wigner rotation and the fractional Fourier transforms[J].Opt.Soc.Amer.A,1993,10(10):2181-2186.

[6]王金婵,赵永安.分数傅立叶变换的进展与展望[J].应用光学,2003,24(5):5-6.

[7]UNNIKRISHNAN G,JOSEPH J,SINGH K.Optical encryption by double-random phase encoding in the fractional Fourier domain[J].Optics Letters,2000,25(12):887-889.

[8]NISHCHAL N K,UNNIKRISHNAN G,JOSEPH J,et al.Optical encryption using a localized fractional Fourier transform[J].Optical Engineering,2003,42(12):3566-3571.

[9]ZHU B,LIU S,RAN Q.Optical image encryption based on multifractional Fourier transforms[J].Optical Letters,2000,25(16):1159-1161.

[10]何俊发,李俊,王红霞,等.不对称离散分数傅里叶变换实现数字图像的加密变换[J].光学技术,2005,31(3):410-412.

[11]张兆祥,田沛,范瑾,等.基于分数阶傅立叶变换的图像加密研究[J].仪器仪表用户,2007,14(5):87-88.

[12]王银花,柴晓冬,周成鹏,等.基于分数傅里叶变换的混沌图像加密方法[J].计算机工程,2007,33(12):172-174.

[13]BANGHE ZHU,SHUTIAN LIU,QIWEN RAN.Optical image encryption based on multifractional Fourier transforms[J].Optics Letters,2000,25(16):1159-1161.

[14]MENDLOVIC D,BTTRAN Y,DORSCH R G,et al.Anamorphic fractional Fourier transform:Optical implementational application[J].Applied Optics,1995,34(32):7451-7456.

[15]SAHIN A,OZAKTAS H M,MENDLOVIC D.Optical implementation of the two-dimensional fractional Fourier transform with different orders in the two dimensions[J].Optics Communication,1995,120(3):134-138.

[16]XIAOGANG WANG,DAOMU ZHAO.Image encryption based on anamorphic fractional Fourier transform and three-step phase-shifting interferometry[J].Optics Communications,2006,268(2):240-244.

[17]王红霞,赵玮,刘长文,等.基于变形分数傅里叶变换的六重密钥图像加密[J].光子学报,2007,36(4):759-761.

[18]林睿.采用变形分数傅立叶变换的光学图像加密[J].重庆工商大学学报:自然科学版,2006,23(3):289-291.

[19]ALPER KUTAY M,HALDUN M.OZAKTAS.Optimal image restoration with the fractional Fourier transform[J].Opt.Soc.Am.A,1999,20(6):452-453.

[20]刘正君,赵海发,朱邦和,等.分数傅立叶域数字水印算法[J].光子学报,2003,32(3):332-334.

[21]丁卫平,刘喜斌.分数傅立叶变换的光学实现及其应用[J].湖南理工学院学报:自然科学版,2005,18(3):9-12.

[22]曹玉茹,张子云,韦穗.分数傅里叶全息图的快速算法及数字重现[J].计算机工程与应用,2005,41(27):19-22.

[23]LOHMANN A W,MENDLOVIC D.Fractional joint transform correlator[J].Appl Opt.,1997,36(35):7402-7407.

[24]WEAVER C S,GOODMAN J W.Technique for optically convolving two functions[J].Appl Opt,1996,5(5):1248-1249.

[25]DAVID MENDLOVIC,YIGAL BITRAN,RAINER G DORSCH,et al.Anamorphic fractional Fourier transform:optical implementation and applications[J].Appl.Opt,1995,34(32):7451-7456.

[26]朱邦和,韩立.基于分数傅立叶变换的分数相关峰值特性[J].光子学报,1999,28(10):910-912.

[27]韩立,刘树田.分数相关畸变不变模式识别特性研究[J].光子学报,2000,29(2):131-136.

[28]王金婵,赵永安,王西安.应用联合分数傅立叶变换相关器识别多个物体[J].光子学报,2002,31(6):681-684.

[29]窦德召,常鸿森,林睿.变形分数傅立叶变换相关器[J].华南师范大学学报:自然科学版,2005(3):70-73.

[30]孔敏龙,代明.光学谐振腔的分数傅里叶变换表示[J].激光技术,1998,22(1):29-33.

[31]许晓军,陆启生.分数阶傅立叶变换在球面谐振腔稳定性分析中的应用[J].应用激光,2000,20(4):149-151.