基于训练任务的舰炮备件短缺风险建模与仿真研究

徐廷学，魏 勇

（海军航空工程学院 a.兵器科学与技术系；b.研究生管理大队，山东 烟台 264001）

0 引言

备件作为保障资源中不可或缺的资源，备件的库存对装备的保障能力起着至关重要的作用。能否及时有效地提供所需备件，直接关系着维修保障工作的开展。例如，美军于1977年在胡德堡进行了一次大规模野外演练，其中装甲车辆备件保障暴露出非常严重的问题。演练中需要78种备件，而只有27种有储备，51种（占65%）未列入备件储备清单目录。此外，演练前计划的备件有376种，而实际使用中有93%未用到，这不仅影响了装备维修工作的开展，而且储备这些不必要的备件对维修单位来说是个沉重的负担。

从收集的近几年装备备件的储存数据来看，一些装备备件的储存也不是非常合理，有些零件价格昂贵，但在装备全寿命过程中只损坏1～2次，而其备件却储存了不少，这样不仅占用了大量的保障费用，增加了备件库存管理费用，而且当装备有所变更或其某些组元被淘汰时，大量储存的备件就有成为“死货”的危险；而对有些易故障的零件，其备件却配置得不够甚至没有配备，一旦零件故障就容易导致装备无法使用，造成不可估量的损失。

因此，和库存相关的参数，例如备件短缺风险（Risk of Shortage，ROS）、延期交货量（NBO）、备件需求量（NS）等参数被用来反映备件库存水平的关键程度或不能完成任务剖面中任务的程度。其中，由于备件短缺风险能很好的衡量库存满足需求的能力，反映保障系统的保障能力，所以，选取备件的短缺风险作为衡量保障系统保障能力的参数指标是合理的。它不但能评估备件的保障能力，还可以作为评估完成训练或作战任务能力的指标。

当前，对备件的需求、保障概率、库存优化等内容研究比较多，而对备件短缺风险研究的文献还很少。

文献[1]使用更新过程理论研究了备件保障度评估与备件需求量的模型，给出了部件寿命服从不同分布（指数分布、威布尔分布、正态分布和Γ分布）情况下，单不可修部件的备件保障度模型，然后给出了多不可修部件和多可修部件的备件保障度模型。

文献[2]综述了指数寿命件、威布尔寿命件、正态寿命件和战损情况下备件供应模型，给出指数寿命件计算模型在地面雷达备件供应中的应用。

文献[3]通过使用可用度公式的推导，给出了基于使用可用度的航材备件预测模型及需求分析。这些研究大多数仅考虑装备平时或静态的维修保障能力评估与备件需求问题，没有针对具体的任务过程，而是根据保障资源的种类、数量、经验等对与备件相关的参数进行评估。本文通过对舰炮执行训练任务的描述，考虑任务过程中的动态随机因素，由备件保障概率模型建立备件短缺风险模型，根据给定的任务方案和备件库存方案对备件的短缺风险进行动态评估，研究不同任务时刻、不同库存方案下备件库存短缺情况，最后给出在整个任务时刻备件库存短缺的平均值，并对两个库存方案下备件短缺风险进行比较。计算实例结果表明，根据任务计算的备件短缺更能反映备件库存方案对舰炮装备完成任务的能力的影响。

1 任务剖面模型

任务一般为复杂的多阶段任务，存在着诸如任务时间、任务模式等问题。对任务的描述应具有一定的层次性，即总任务描述和子任务描述。总任务描述是指对任务开始前装备的数量、任务总时间、任务剖面等任务因素的描述；子任务描述是指对任务内容、任务开始时间、任务成功条件等约束条件的描述。

复杂使用任务是由一系列基本任务顺序执行完成。为了问题的简化和分析，按多阶段任务系统（Phased-Mission System，PMS）的概念[4]，任务通常可以按时序划分为一系列时间连续且不相互重叠的任务阶段，一般可用串联、并联关系表示，且每个任务阶段有不同的任务可靠性要求。各个任务阶段在任务系统配置（需要使用不同的功能系统）、任务成功的判据、故障判据及单元故障特性（单元故障率等）等方面会不同。

平时，舰炮主要完成两类任务：日常训练任务和演习任务。由于演习任务时间的不确定性，这里仅研究舰炮（二类舰艇）的典型日常训练任务剖面，如图1所示。

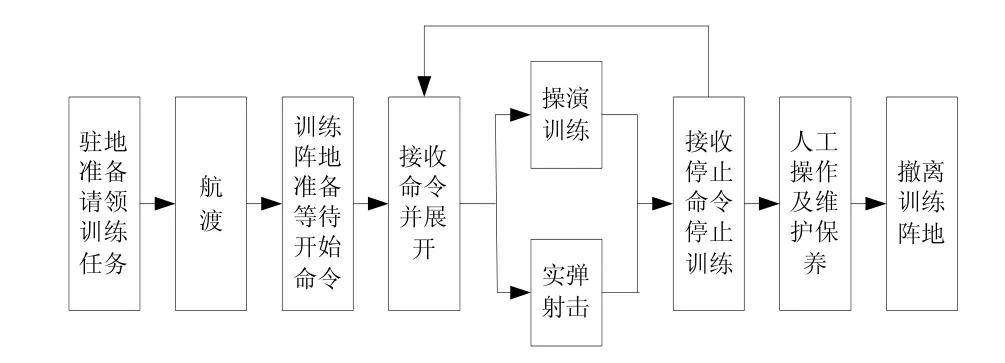
图1 舰炮训练任务剖面图

舰炮大部分时间处在部队的训练状态，在各单项和综合训练中对装备所产生的磨损和损耗是影响装备寿命和保障性的重要因素。一般情况下，舰炮平时训练是不允许带故障进行操作训练的，无论出现什么故障均应排除，恢复正常后，方可进行训练，因此，训练任务保障性要求接近基本保障性，在确定保障性的基本指标时，应考虑训练任务的要求。舰炮典型日常训练任务分为操演训练和实弹射击训练两类，每类训练内容分为一科目、二科目和全训考核3种。

2 备件库存模型

现役装备一般采用的是三级维修保障体制，即舰员级、中继级和基地级。每一级别都配备有相应的维修机构和维修器材仓库。舰炮装备作为保障系统的保障对象产生对维修资源的需求。保障系统的舰员级维修，对应于部队（团及以下单位，一般以一艘舰艇为单位）的舰炮使用人员和舰上的维修技术人员；中继级维修对应舰艇支队级的舰船装备技术保障大队或修理所；基地级维修对应于海军级的修理厂或舰炮研制、生产单位。这三级维修主要负责对故障单元的修理或报废。舰员级库存负责向舰炮装备提供所需的备件，而且接收舰员级维修修复后的故障件作为备件储存；中继级库存负责向舰员级库存供应所需备件，接受中继级维修修复后的故障件作为备件储存；海军总库负责向舰员级或中继级库存供应所需备件，接收基地级维修修复后的故障件作为备件储存，而且承担备件的购置任务。舰炮装备维修保障系统组成如图 2所示。

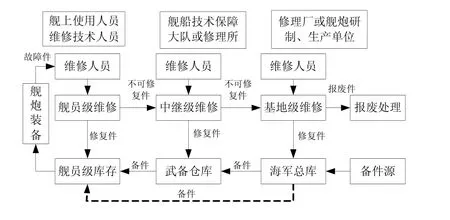
图2 舰炮装备维修保障系统模型

在维修站采用子产品更换来进行维修的产品或系统都会产生对备件的需求。然后，这一需求被传送到其他站点直到找到可以对该子产品进行修复的站点为止。然后备件会从库存中调出进入保障链，并被送往源站点。由于舰炮故障，对故障舰炮进行更换时，可能产生备件库存量不能满足任务需求，从而最终影响舰炮的维修和战斗任务。因此，为了满足任务要求就需研究备件的库存量，本文考虑三级库存：舰员级仓库、基地级备件库（武备仓库）和海军级备件库（海军总库）。假定这三级备件库的实际库存量等于初始库存量，重点研究实际库存量小于初始库存量的情况。

3 备件短缺风险计算模型

ROS是检验库存满足需求能力的指标，定义为在每个库存点备件库存量不能立即满足需求的概率，其从另一方面反映了备件库存量满足维修保障的水平，可称为非保障概率，因此可以通过保障概率P 计算，即ROS=1 −P。备件保障概率定义为：对于整个作战单元，在规定的任务时间内，当需要备件时能够在规定的时间内获得相应种类和数量的备件的概率。

以备件整体为研究对象，以舰炮备件库存系统的实际管理要求为基础，本文提出了对于备件短缺风险的仿真计算模型。

应用Barlow的理论和方法：Barlow将部件及其备件看作冷储备子系统，将整个备件系统看作各子系统的串联构成的系统，该储备—串联系统的可靠度作为备件库存系统的保障概率。在实际中，当舰炮上某个或者某几个部件出现了故障，如果备件库存有所需备件，可及时更换，舰炮可以正常运行；如果备件库没有所需部件的备件，就造成了缺件。通常，备件库存的保障概率用备件库的服务水平来定义[5-6]：

由上式可知，备件保障概率相当于单个部件保障概率的代数平均。

从保障概率的概念出发构造一个评价函数。由上式可以看出，总的备件保障概率可认为是申请备件时能够及时提供的概率。用 Ni(t)，(i=1,2,…,n)表示在(0,t)时间段内第i种备件发生故障需要更换的次数，xi表示第i种备件配置的备件数。于是：

第i种备件的保障概率 Pi为：

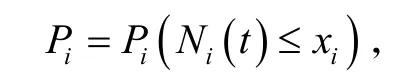
则整个备件库的保障概率P为：

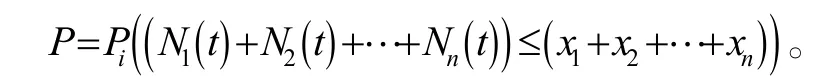
上式是根据备件保障概率的基本定义构造的保障概率模型，从这个基本定义式出发继续推导它的内在形式。

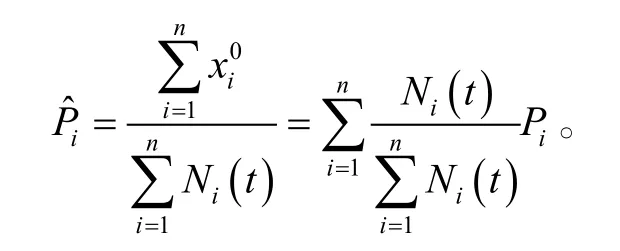
引入iλ 作为第i种部件出现故障的概率，由更新过程理论[7]可得：

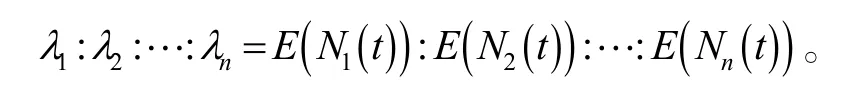
对于部件寿命服从指数分布的情况，上式精确成立；对于部件寿命是非指数分布的情况，上式渐近成立（证明略）。

按照备件是否可以修复将其分为可修复件和不可修复件。修理故障设备时，若失效件是不可修复件，从库存中拿出备件进行更换并按照运行规则补充库存，失效件报废处理；若是可修复件，先从库存中拿出备件进行更换，失效件进行修复后再放回库存。如果可修复件有一定的修复率（或者修理时存在一定报废率），则意味着其中有一定比例不能修复，相当于不可修复件。

研究备件库存系统时，无论是可修复件还是不可修复件或者是有一定修复率的备件，可以统一地认为对失效件进行更换从而使设备故障和备件需求建立直接的联系，不同点在于更换可修复件同时触发了一个提前期为修理周期的订单，而更换有一定修复率的备件，相当于按照比例触发修理订单。

3.1 不可修件短缺风险

在此基础上给出不可修备件保障概率。为简化备件的计算，均假定单位时间内备件的需求数服从参数为λ t的泊松分布，即部件的寿命服从指数分布，则在(0,t)时间内第i种备件正好需要 ki个备件的保障概率为：

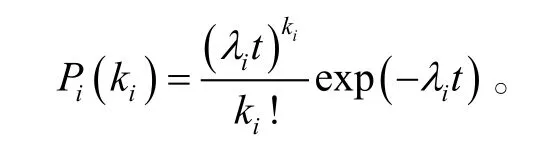
则单备件的保障概率模型为[8]：

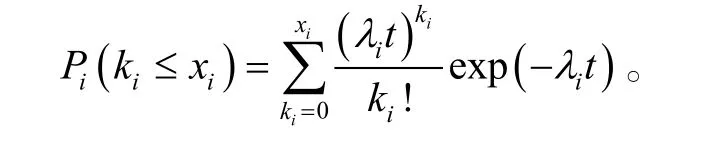
所以得到总的备件保障概率模型：

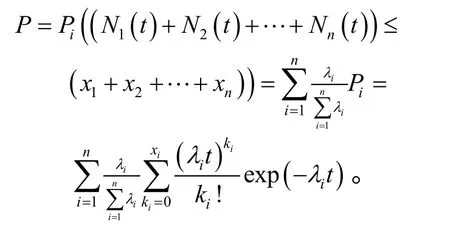
由此得备件的短缺风险：

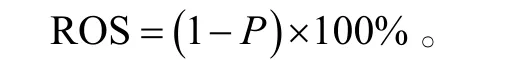
3.2 可修件短缺风险

对可修复类型的备件由于其修复后可再生，能提高维修器件的利用率。因此，在其他条件一致下，所需备件的数量相应有所减少。在建立数学模型时，考虑备件的维修性，其系统结构如图3所示。

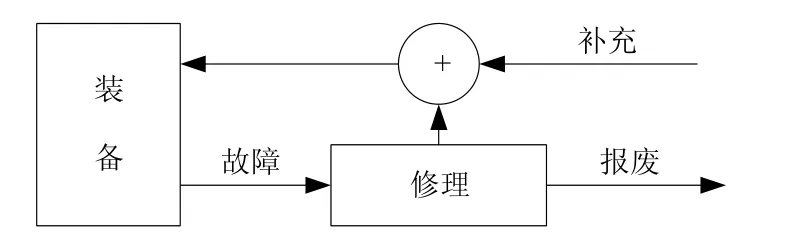
图3 可修复类型备件模型

该系统可看成是多服务台M/M/c（L+N）的排队系统，可维修备件的故障和修复时间均服从指数分布。假设各维修分队工作相互独立且平均服务率相同，当工作部件出现故障，就立即用备件替换下来；如没有备件，装备停止工作，由维修分队进行修理，修好后作为备件可重新使用。从而备件保障度评估问题转变为有限源排队系统中可工作部件大于等于L的概率求解问题。根据排队论的方法得出在任务期间第i种备件正好需 ki个备件的概率为：

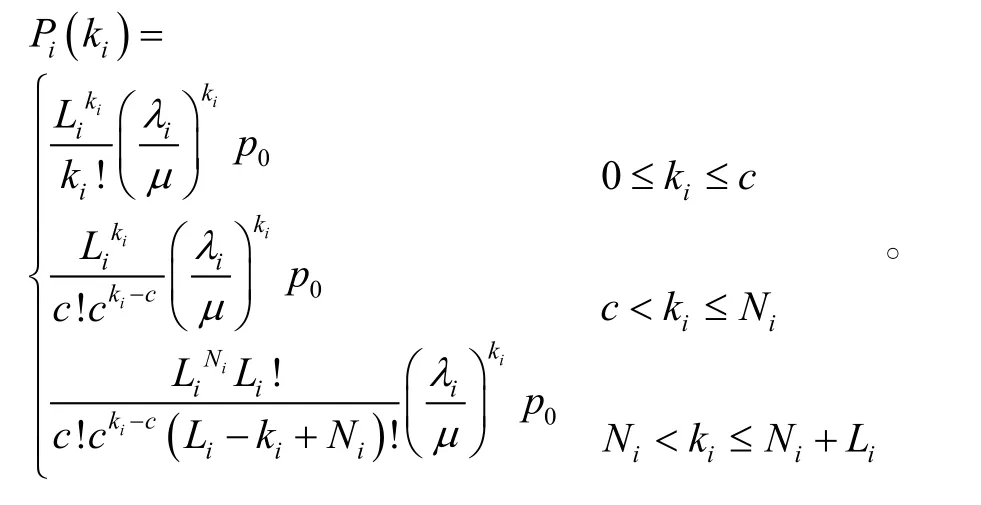
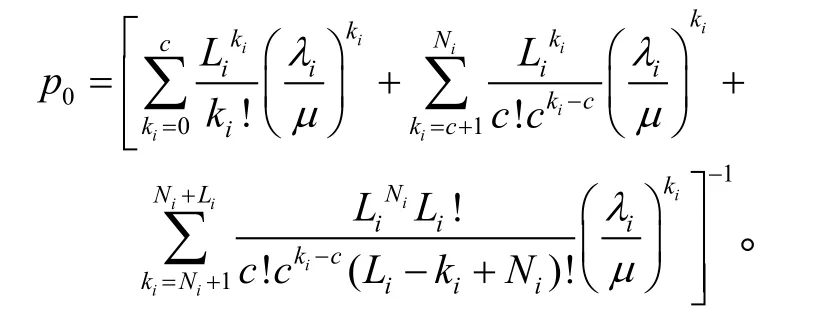
第i种备件配备Ni个备件的任务期间备件保障概率即等于备件需求小于等于Ni的概率。因此，当发生维修事件时，该系统中某装备上某备件的不缺货概率为：

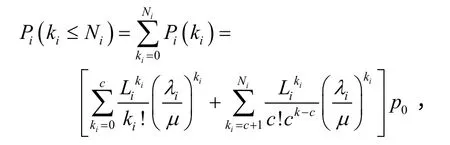
所以，总的保障概率为：

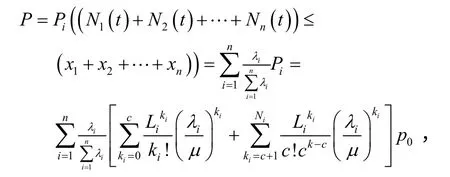
式中：Li为舰炮装备上第i种可维修部件的数量；Ni为第i种备件配置数量；λi为i种可维修部件的故障率；c为维修分队数量；µ为维修分队的平均服务率；p0为初始状态概率。

由此得备件的短缺风险：

ROS=(1 − P)× 1 00%。

4 仿真实例分析

以一个作战单元2艘二类舰艇舰炮为例，认为除备件资源以外的其他保障资源是给定的且是充足的备件有400种，每种备件在各个库存点的储备量在[0，9]间取值，可修复件的修复率为1，不可修复件在故障后直接在相关的站点进行更换。

假定该作战单元在年度××个训练日内完成一科目和二科目的部署转换、备战备航、对海射击操演、对空射击操演等相关任务，具体数据如表1、2所示。

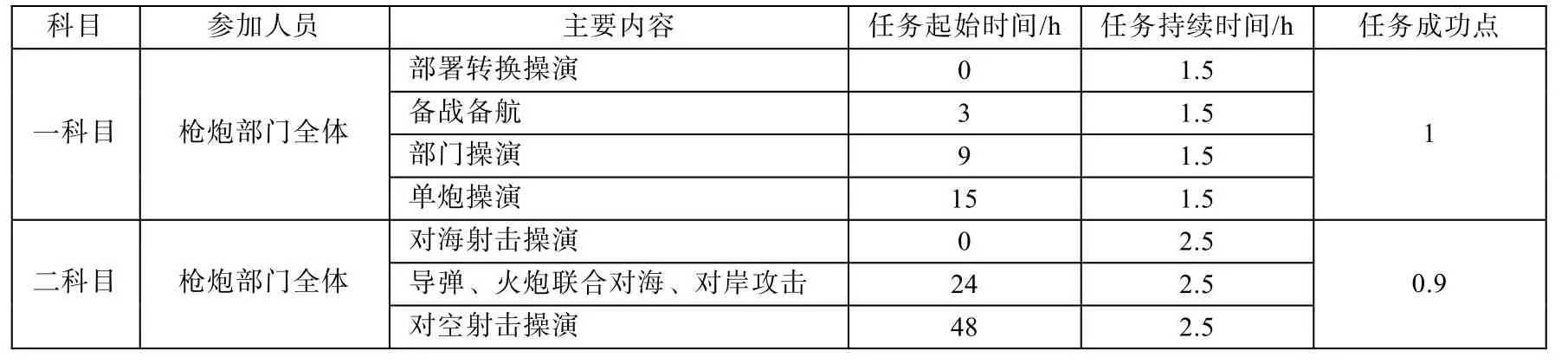
表1 任务剖面表

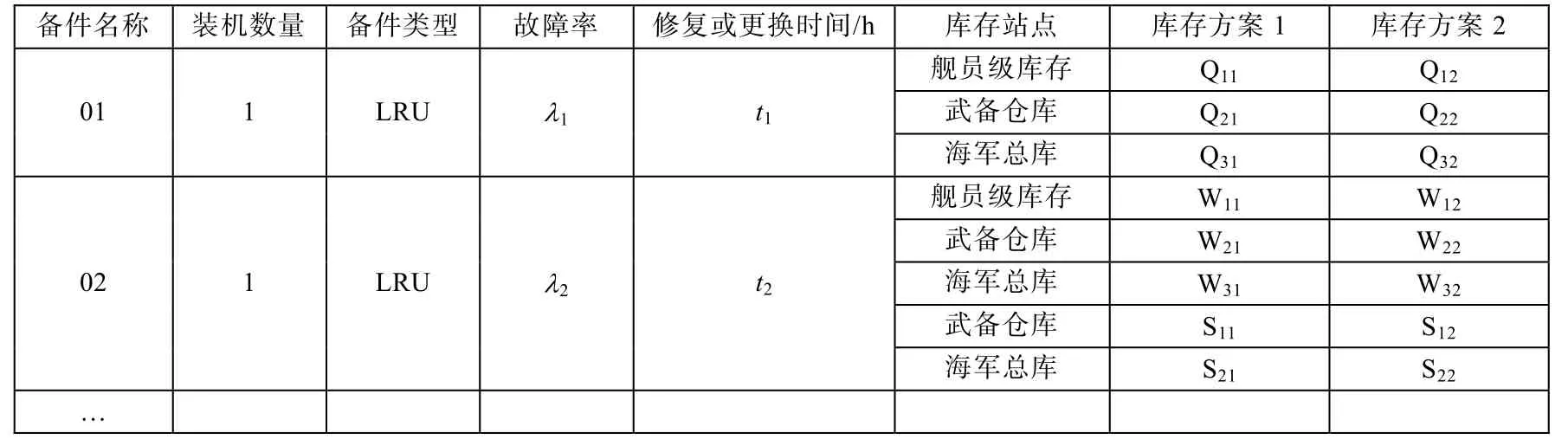
表2 备件库存表

现根据上述情况，应用库存方案1对该作战单元在执行相关任务时的备件短缺进行仿真。由于两艘舰艇在执行任务期间共享备件资源，且备件的缺货是随机的。因此，本文利用离散事件的蒙特卡洛法仿真建立的评估模型，仿真周期为1 440 h，随机种子为123 456 789，则本次仿真结果如图4所示。

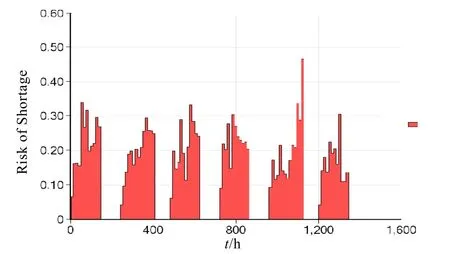
图4 方案1 下备件短缺风险仿真图

对上图的仿真结果求平均值得到整个单元在执行任务期间备件的短缺风险，如图5所示。

图5 方案1 下备件短缺风险仿真平均值

假定库存方案 2的舰员级备件库存量是在库存方案 1 舰员级库存量的基础上加 1 得到，其他仿真条件不变，则本次仿真的结果如图 6所示。对图6的仿真结果求平均值得到整个单元在执行任务期间备件的短缺风险，如图 7所示。

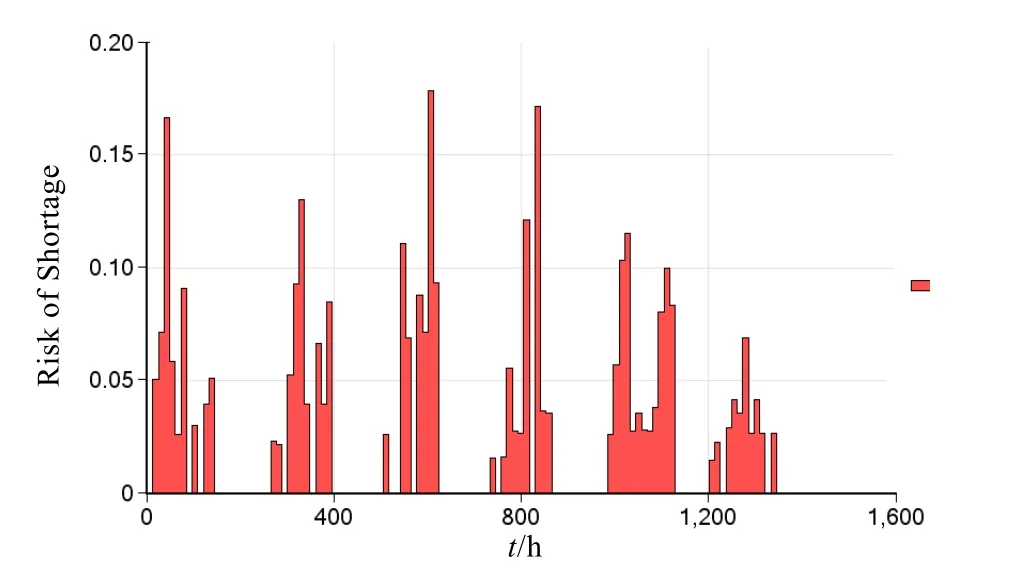
图6 方案2 下备件短缺风险仿真图

图7 方案2 下备件短缺风险仿真平均值

比较图4、5与图6、7，可以得出：增加舰员级的备件库存量可以有效降低备件的短缺风险，从而可以增加训练任务的成功率，这与实际情况是相符的，证明了仿真方法的正确性。必须指出的是：在武备仓库和海军总库两级仓库备件供货正常的情况下，增加这两级仓库的备件库存量，同样可以得到相同的结论。

5 结论

本文依据舰炮典型任务，从研究备件保障模型和备件保障概率出发，以备件短缺风险作为评价备件库存量指标，给出了不可修备件和可修备件的短缺风险计算模型，这为某任务假定下的舰炮装备备件库存方案的制定提供一定借鉴作用。

本文中任务时间均为假定，部件更换时间假定为相同，部件寿命服从指数分布，且未考虑备件的维修，而实际中，担负训练任务的舰炮装备，各类部件寿命分布不同，更换时间差别较大，许多部件可修复后继续使用。因此，下一步可开展复杂任务情况下寿命分布服从一般分布条件的备件短缺风险的研究。

[1]张建军,李树芳,张涛,等.备件保障度评估与备件需求量模型研究[J].电子产品可靠性与环境试验,2004(6):18-22.

[2]杨秉喜,张义芳,熊勇.备件需求量计算模型及其在地面雷达中的应用[J].电子产品可靠性与环境试验,2000(6):13-17.

[3]刘照青,刘洋,王端民.基于使用可用度的航材备件预测模型及需求分析[J].航空计算技术,2007,37(5):38-41.

[4]姜朝毅,于永利,张柳,等.基于Petri 网的装备系统任务成功概率仿真[J].计算机仿真,2006,23(1):29-32.

[5]瞿红春,孙春林.一种基于航材系统保障率的备件可靠性模型[J].航空维修与工程,2004(3):50-51.

[6]伏洪勇,赵宇.一种航空设备备件预测模型的风险评价[J].系统工程与电子技术,2003,25(12):1576-1578.

[7]DINESH KUMAR U,KNEZEVIC J.Availability based spare optimization using renewal process[J].Reliability Engineering and System Safety,1998(59):217-223.

[8]BLANCHARD B S.A key to effective serviceability and maintenance management[M].Indianapolis:John Wiley&Sons,Inc,1994.