数据可视化处理的数学模型

崔汝麦，司守奎

（1.威海职业学院，山东 威海 264210；2.海军航空工程学院 基础部，山东 烟台 264001）

随着信息科学与各种测量技术的发展，在气象、医学和探矿等领域产生了海量的数据。由于缺乏有效分析手段，常常要舍弃庞大数据群中的大部分数据。人们迫切希望对数据进行更高层次的分析，揭示其隐藏的重要信息，以便更好地利用它们。数据可视化就是顺应这一趋势而发展起来的，对原始数据信息进行可视化处理后，抽象繁杂的数据变得直观简单、生动有趣[1]。

1 问题提出

本文研究的问题源于一个实际问题。该问题提供了来自某空间区域8个水平截面上各对应点某物理量的实际测量数据。

要求直观分析出该物理量在这一空间区域的分布情况，具体要求如下：

1）提供该物理量在各截面的分布情况；

2）提供该物理量在整个空间区域的分布情况。

参考数据如表1所示，其中，500p,…,1200p分别代表8个水平截面的z坐标值，每个水平截面下有3组数据，分别表示测量点的x坐标、y坐标和测点处的某物理量的观测值。

表1 问题的数据

2 模型的建立

2.1 建模的思路

根据所给的数据分布情况，通过平移与旋转对研究区域的数据进行标准化处理，并对该区域进行网格划分。再进行二维插值运算，计算出每个网格数据，并对 8个截面进行可视化显示。最后进行空间插值，获得空间上的分布数据，并将其显示出来。

2.2 模型假设

1）实测数据均可靠，没有误差；

2）实验数据采集广泛，具有普遍性；

3）所测物理量是连续变化，不存在突变。

2.3 符号说明

2.4 建模

2.4.1 数据处理

问题中8个水平截面上的实际测量数据，实际上是在xy 平面上取若干个点，然后分别测量这些点在8个水平截面上的值。这些点在xy 平面上的位置如图1所示。

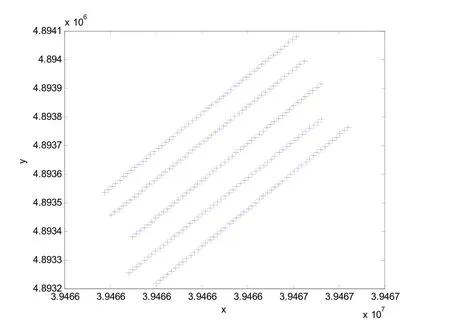
图1 测量点的水平分布

从图1中可以看出，这些点大致均匀分布在五条直线上，即所给数据是在这五个竖直截面上分别测量8个水平截面上的值。为了获得物理量在各截面和整个空间区域的分布情况，显然我们需要根据这些数据进行插值。

如果直接在图示范围内进行插值计算，不仅计算量大，而且四个边角上的插值误差很大，实际意义不大。为获得有效数据并减少计算量，我们可以先对坐标轴进行平移与旋转处理，将这些测量点平移旋转到一个较小的矩形区间，然后再进行计算。

平移与旋转变换之后测量点x轴上最大值与最小值的差值为1 080，而y轴上最大值与最小值的差值不到390，两者比例为2.769，我们在保持原测量点的位置比例不变的情况下进行位置数据标准化处理，相当于将包括全部测量点的最小立体区域从原来坐标系中取出，并保持长宽比例2.769，然后重新建立坐标系，这样就减小了x轴和y轴上数值的量级，简化了计算。

标准化计算公式为

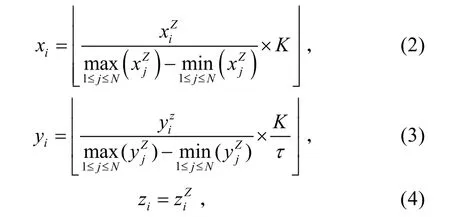
式中：N为测量点的数量；K为x轴上划分网格的数量；τ为测量区域矩形的长宽比例；L表示取不大于L的最大整数，取整主要是为了后面插值划分网格的方便。

在选定的矩形中每条直线在横向上都不能到达矩形区域边线；如果直接进行网格划分并插值，将会出现在某些点的插值为不确定值，这就要缩小矩形再进行网格划分和插值，从而造成部分数据丢失，而不能充分利用现有信息。所以我们先采用一维三次样条插值，将缺少的点插值获得再进行后面的计算。插值补全处理之后的效果如图2所示。

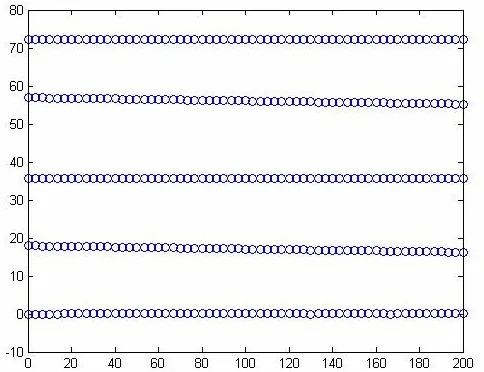
图2 插值补全处理

2.4.2 网格细划

针对原始数据点分散，数量不足等问题，首先对所给空间进行网格细划，通过二维插值来获得各网格点上的物理量值，提高数据密度，再进行空间插值，可得到可视化图。

将转换后的较小立体区域划分为200×72×70个小网格，然后分两步进行插值计算。

第一步：取出 8个截面中的一个，根据原始数据，采用三次样条插值的方法，插值计算出该截面上200×72个网格上的数据。同样对其他 7个截面进行相同的计算，从而获得200×72×8个网格上的数据。

第二步：取出一个竖直截面，其网格数为200×70；从上一步求出的数据中取出在该截面上的200×8个网格的数据，同样进行三次样条插值计算，插值计算出该截面上所有网格的数据。同样对剩下的71个截面进行相同的计算，从而获得所有网格的数据。

通过插值，估计出某一点缺失的测量数据，提高了数据密度；也使数据网格化，把非规则分布的空间数据内插为规则分布的空间数据。

2.4.3 空间插值

空间插值[2-4]是指通过已知的数据点或已化为各个相对小一些区域内的数据点，计算出相关的其他未知点或相关区域内所有点的方法。根据网格细划所得的数据，可以分别采用以下插值方法计算。

1）最近邻点插值法充分利用了插值点与已知点之间的距离关系，反映了实际情况，但造成变量值的高估或低估，产生不光滑表面。

2）三线性插值法能缓解边界不连续、改善表面不光滑的问题，但使锐度明显的边缘变模糊。

3）三角网/线性插值法能充分利用已知点的信息，且表面光滑，但其等值线呈现锯齿状。

上述 3种插值方法各有优缺点。经充分比较运算，可将最近邻点插值法、三线性插值法和三角网/线性插值法以1∶2∶4的比例加权平均，设计出综合插值法，能够充分发挥 3种方法的优点。以截面600p所给数据为例，此模型立体表面光滑，等值线[5]也较平滑，效果见图3、图4。

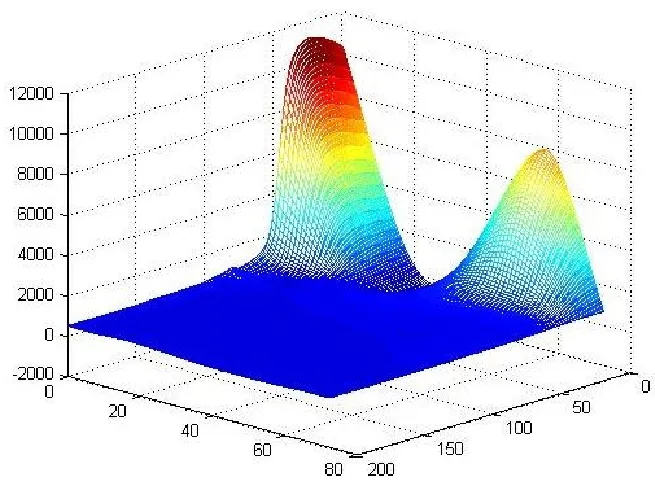
图3 综合插值法立体图

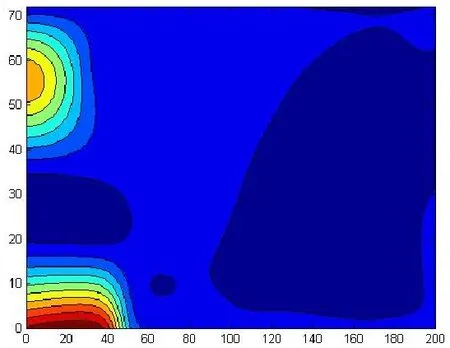
图4 综合插值法等值线图

3 问题解答

3.1 截面上的分布

根据本文设计的综合插值法模型，可插值计算出所测物理量在各截面的分布情况，见图5、图6。从截面500p～900p的分布图可以看出，该物理量的大值主要分布在矩形区的左上和左下角区域；而且随着竖直方向值的增大，大值分布在朝下方移动。而从截面1 000p～1 200p的分布图可以看出，物理量的分布较为广泛，但随着竖直方向值的增大，物理量集中于研究区域左下方的分布情况更为明显。

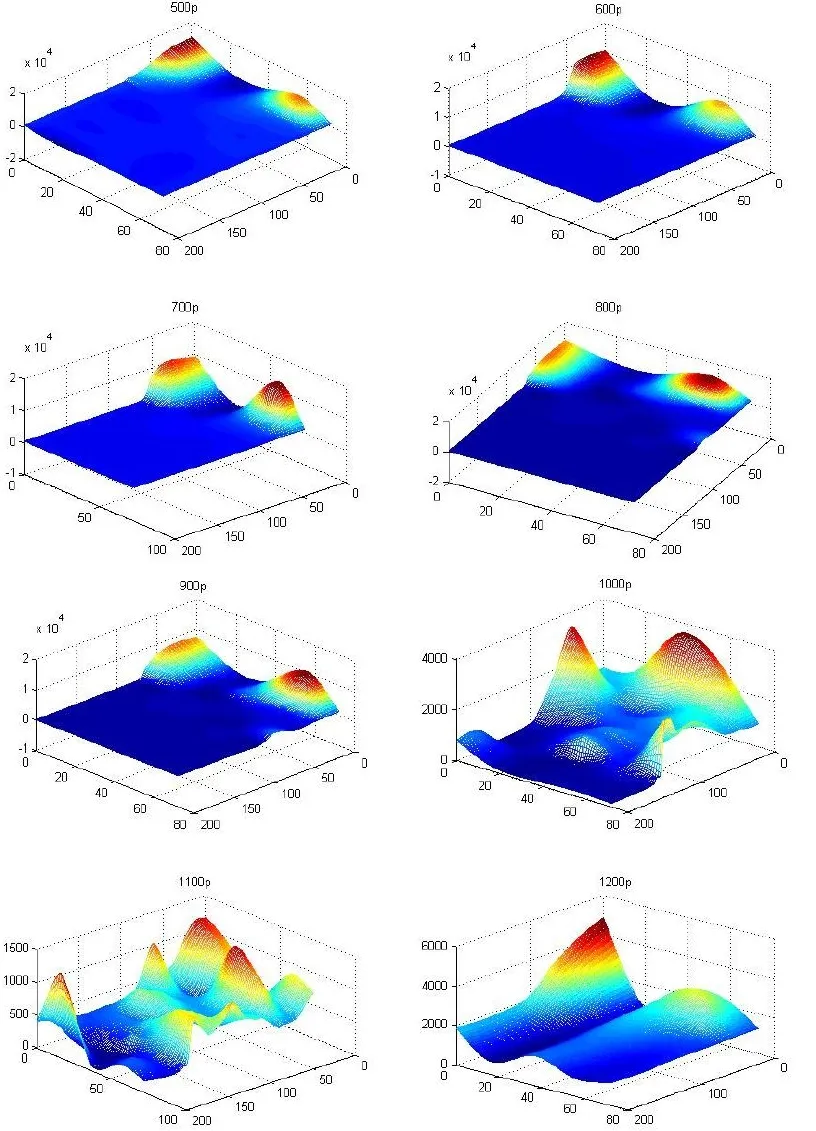
图5 物理量在8个截面的分布图

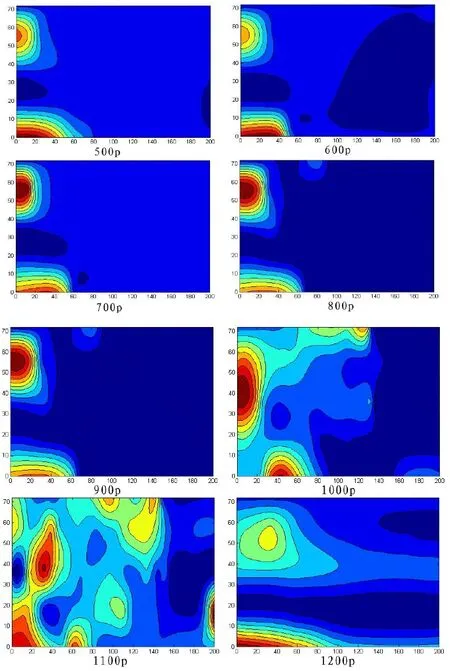
图6 物理量在8个截面的分布等值线图

3.2 空间区域的分布

依据网格细划中提出的两个步骤，采用综合插值法计算出所有小网格的数据。使用Matlab[6-7]中的griddata3命令，获得空间区域的分布情况，如图7、8是其中的2个截面图。图7、8能较为明显地看到物理量的大值集中分布情况，也证实了我们上面的分析。在实际应用中，可根据要求具体分析某个截面的分布情况，从而为正确决策提供科学的支持。

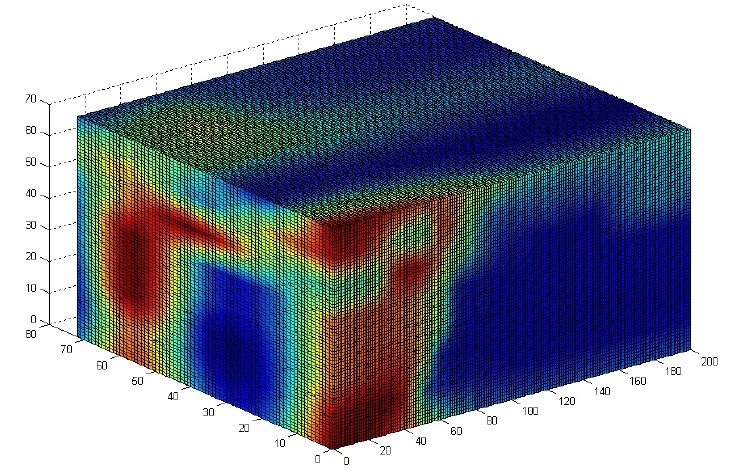
图7 空间区域的分布截面

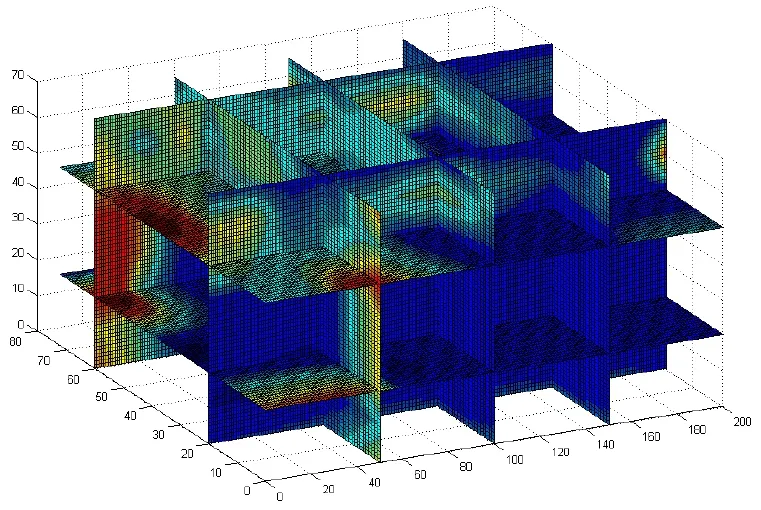
图8 空间区域的分布截面

4 模型的评价与改进

本文针对分布不均匀、数据点不足的复杂数据建立了可视化处理的数学模型，为科研工作者进行类似工作时提供了一定的参考依据。

本模型适应性广，但计算精度要依据数据的离散程度和网格划分的细密程度两个方面。其中，网格划分越小，精度也就越高，但计算量就会大为增加，设计时要兼顾二者的平衡。其次，如果数据是均匀分布的离散数据或者能够对特定点测量后再进行插值计算，可简化计算，提高精度。

[1]唐泽圣.三维数据场可视化[M].北京:清华大学出版社,1999.

[2]颜慧敏.空间插值技术的开发与实现[D].成都:西南石油学院,2005.

[3]叶其孝.大学生数学建模竞赛辅导教材[M].长沙:湖南教育出版社,2001.

[4]萧树铁.数学实验[M].北京:高等教育出版社,1999.

[5]王智刚,唐瑶,曾向红,等.雷电灾害数据可视化分析系统研制[J].气象,2009(5):23-30.

[6]张宜华.精通MATLAB5[M].北京:清华大学出版社,2000.

[7]王家文.MATLAB6.5 图形图像处理[M].北京:国防工业出版社,2004.