引进装备备件可靠性及保障研究

孙建国，夏长俊，赵修平，倪保航

（海军航空工程学院 a.新装备培训中心；b.飞行器工程系，山东 烟台 264001）

引进装备不像国产装备那样，在国内有着顺畅的供应保障链，对它们的维修、保障对国外的依赖性是显而易见的。备品备件是武器系统维修保障所必需的，是保障武器系统发挥战斗力的重要组成部分。但是，由于引进装备武器系统所需的大部分备品备件还需要从国外进口，所配备的备件数量还受外方制约。因此，对引进装备武器系统备品备件储备量的研究是非常有意义的。对引进装备武器系统备品备件储备量的研究就是要确定既能满足维修引进装备武器系统所需的备件数量，又不会造成库存备件积压，节省费用开支[1-2]。本文是根据引进装备的管理保障要求，以可靠性、维修性理论为基础，针对引进装备武器系统可靠性、维修性特点，结合数理统计的知识，对备品备件的需求预测方法进行新的探索，进而建立一种较为实用的备品备件需求预测模型，并用经济订货批量模型的原则建立了引进装备的订货方法。

1 备品备件及其分类

在装备维修工作中，为了恢复装备的性能和精度，需要用新制的或修复的零部件来更换已受损的旧件，通常把这种新制的或修复的零部件称为配件。为了缩短修理时间或增加战备完好性，对某些因形状复杂，要求高，加工困难，生产（或订购）周期长的零部件——配件，在仓库内预先储备一定数量，这种配件称为备品备件，简称为备件。

备品备件有多种分类方法：按维修性分类，可分为可修件和不可修件，或消耗件和周转件；按ABC 分类法，可分为A类备品备件、B类备品备件和C类备品备件；按备品备件的传递能量，可分为机械备品备件和电器备品备件；按备品备件的来源，可分为研仿备品备件、替代备品备件和外购备品备件，引进装备的备品备件，几乎全部为外购的。

2 装备备件的可靠性

2.1 可靠性定义及可靠性指标

可靠性是指产品在规定的条件下和规定的时间内，完成规定功能的能力。所谓产品，可以是一个小的零件，也可以是一个大的完整系统。在本论文中主要是对可以单独进行拆换、维修的引进装备可靠性进行研究。

一般来说，可靠性指标分为3类：用概率计量的指标——可靠度函数R(t) 和故障密度函数f(t)；用时间计量的指标——平均寿命和可靠寿命；用单位时间比率计量的指标——故障率，故障率是预测备件需求量的常用指标。

2.2 引进装备的寿命分布参数估计和假设检验

对于进口装备，我们掌握的技术资料不多，性能参数也不完全了解，掌握的性能参数就是我们对进口装备保障的一个基本依据。比如说装备的寿命分布，如果装备的寿命分布类型已知而分布参数未知，我们可以从收集得到的装备使用记录、数据等进行分析、处理，并估计出装备寿命的分布参数。

对装备寿命分布数据的分析处理方法有多种，常用的有两种，第一种是非参数法，通过对数据的分析，得到一个无参数的、以数值来定义的分布，如直方图；第二种是参数估计法，直方图是当样本容量很大的情况下才可以使用，当装备发生故障的时间间隔比较长，样本比较少，可以采用参数估计的方法对装备的可靠性指标进行评定[3]。

在参数估计中，都是在零件寿命分布函数已知的情况下进行的，而有时并不能确定某种零件是否一定属于某种分布。此时，就需要对其进行寿命分布的拟合检验[3]（由使用记录统计到的零件故障数据作为检验样本）。

2.3 电子设备可靠性预计

引进装备中大部分备件都是电子器件，对于这一类设备，可以用电子设备可靠性预计的方法对设备的可靠性进行快速估算。

电子设备均是由电阻、电容、二极管、三极管、集成电路等标准化程度很高的电子元器件组成，而对于标准元器件现已积累了大量的试验、统计数据，已有成熟的可靠性预计标准和手册，比如说，我国的国家军用标准GJB/Z 299B-98《电子设备可靠性预计手册》、美国军标MIL-HDBK-217E《电子设备可靠性预计》等。

2.4 设备失效率的计算

装备失效率定义是：

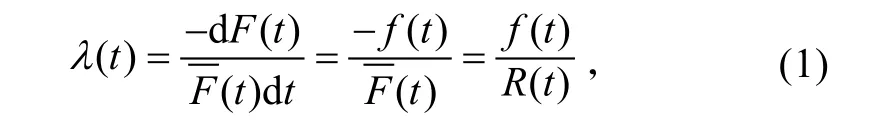
式中：F(t)为故障分布函数；f(t)为失效的概率密度函数；R(t)为可靠度函数。

对于不同寿命分布的装备，其失效率的计算如下：

1）对于寿命服从正指数分布的设备

2）对于寿命服从正态分布的备件

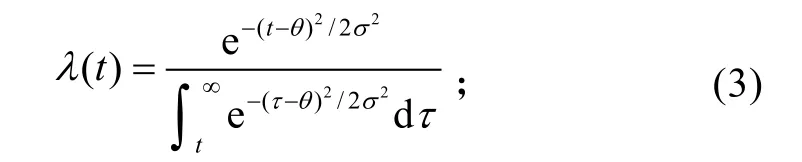
3）对于寿命服从对数正态分布的设备

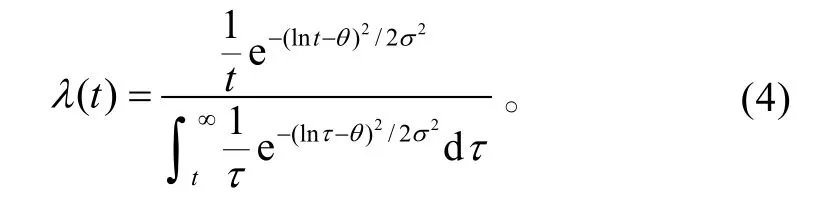
应用上述公式，可以计算出备件的失效率 λ(t)，但是，应用上述公式的前提是必须能够事先确定备件的寿命分布（包括各种参数的确定），这些参数可通过前面叙述的统计分析方法去求得。

3 备件的需求预测分析

结合引进装备寿命分布参数估计、寿命分布假设检验以及电子设备可靠性预计方法，可以根据装备的寿命分布分别预测引进装备备件的需求量[4]。

3.1 指数寿命件备件量计算模型

若装备中某项零部件的寿命服从指数分布，为满足规定保障概率P，该项零部件的备件需求量可按下式计算：

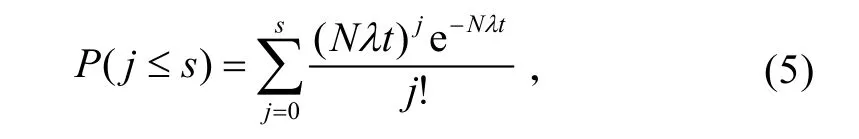
式中：s为装备中某零部件所需备件数量；N为装备中某零部件的件数；λ为装备中某零部件的失效率，10-6/h（假定备件在存放期内无失效）；t为保障时间，保障时间t可按不同情况分别处理；j为递增变量，j 从0 开始逐一增加，直至某s值，使得P（j≤s）大于规定值，该s值即为所求之备件数量；P为备件保障概率，即需要该备件时能得到它的概率。

3.2 正态寿命件备件量计算模型

已知正态寿命件寿命均值E，标准差σ，保障时间t（如果是磨损寿命t 用工作时数，如果是腐蚀，老化寿命t可以用日历时数近似）和需要备件时能得到备件的概率P（保障概率）条件下，单项件（单个可更换单元）备件需求量s为：式中：up为正态分位数，可查正态分布表得[5]。

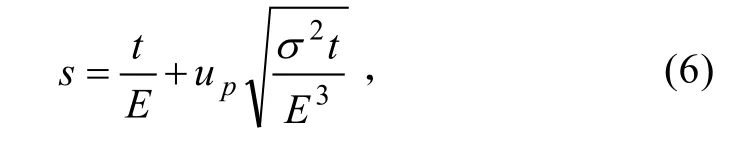
3.3 寿命服从威布尔分布的备件需求量的确定

已知：

1）某部件寿命分布为3个参数威布尔分布：

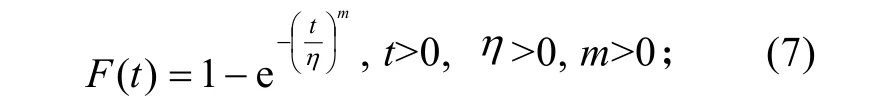
2）需要该部件时，能得到它的概率为P，并设此事件（即“部件故障时能得到满足”）服从正态分布；

3）保障时间t；

4）该部件共有N个在工作；

5）该部件可修复，修复率为µ（当µ=0时，表示该部件不可修）。

在单部装备累积工作时间不大于t，备件满足率为P，需为装备提供该备件的个数s的计算模型如下：

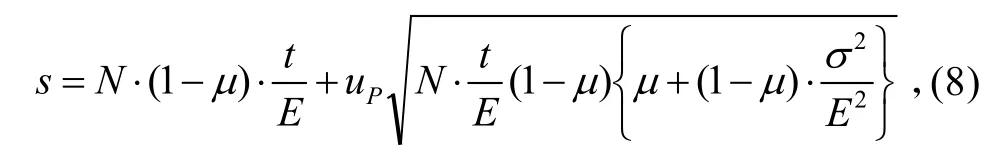
式中：up为正态分位数，可查正态分布表得；E、2σ分别设备寿命的均值和方差，且

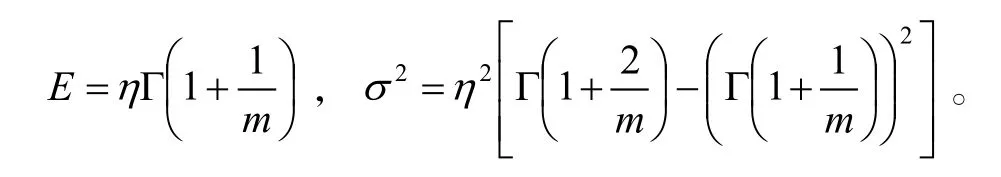
若E、2σ 未知，可用其估计值E、2σ代之。

4 备件库存控制方法

过多的库存对于应付备件的需求可能是很理想的。但是对于昂贵的进口装备，这样会使大量资金积压在库存中，造成很大的浪费；而且还可能出现报废情况，特别是在系统有所变更或其某些部分陈旧淘汰时。反之，若提供的库存量太小，就可能由于库存短缺以致系统无法使用，也会造成损失。一般来说，最理想的是在任何给定时刻的备件库存数量、提出订货单的频数以及每一次订货单订购的件数之间取得经济的平衡，这种平衡可以用经济订货批量方法来解决[6]。由于是引进装备，难以做到按定量法控制订货，因此，采用定期订货法。

定期订货法预先确定一个订货周期T 和一个最高库存量 Qmax，周期性地检查库存，得出当时的实际库存量 Qki，然后发出一个订货量iQ，这个第i次发出的订货量的大小，应使订货后的名义库存上升到 Qmax。

每次订货量的计算公式为：

4.1 订货周期T的确定

1）根据日历习惯确定

例如一个月订货一次或一年订货一次，那么订货周期就是一个月或一年。至于用什么样的时间单位，可以根据具体情况定；

2）根据经济订货周期来确定

订货周期T为：

式中：R为备件的年需求量；c0为每次平均订货费；c1为单位备件单位时间库存管理费。

4.2 最高库存量Qmax的确定

在定量订货法中，把订货提前期内的需求量作为制定订货点的依据，在定期订货法中，则是把订货周期和其后一个订货提前期一起，即T+Tk期间内的需求量DT+kT作为制定 Qmax的依据，已知缺备件风险α，Qmax为：

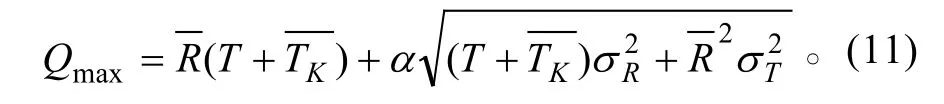
如果DT+kT服从正态分布，则可由下式求 Qmax：

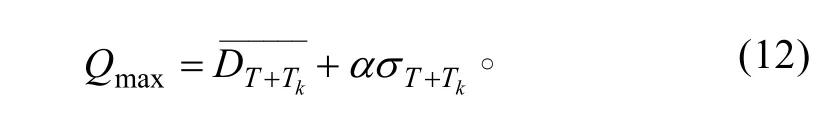
5 装备备件保障软件

进口装备备件的需求预测涉及到大量的数据统计、计算。因此，为了方便快速地得出计算结果，特制做了一款计算机辅助计算软件：装备备件保障软件。软件从设计布置上可以分为5个模块，其名称及功能如图1所示。此软件可根据设备的设计信息计算出设备的故障率，并依据保障时间、保障概率和现在正在使用的设备数量确定出保障时间内所需备件的数量；也可以根据设备前期的故障信息确定出设备的寿命分布，计算设备的平均寿命，并预测在一定的保障时间内所需的备件。

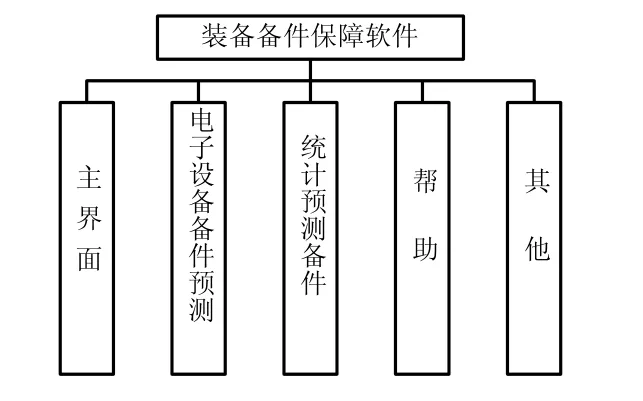
图1 装备备件保障软件结构

装备备件保障软件用Visual C++6.0 设计平台制作，完全采用了面向对象的程序设计（OOP）方法。软件界面友好，使用简便。通过本软件，可使备件需求量预测分析处理过程变得十分简便，备件预测的准确性、经济性都有很大提高。软件基本功能如下：

1）电子设备备件需求量确定

引进武器装备备件大部分是电子设备，它们以分立元件、插板、模块等形式存在着，对它们的需求预测是本课题的重点工作。装备备件保障软件依据备件需求确定过程的原则，把电子设备可靠性预计方法和备件需求预测模型编制成计算机程序，把计算过程所需的数据和公式集成在软件中，这样极大地简化了电子设备备件需求预测过程。使用软件预测电子设备备件的需求量时，要以设备的设计信息为基础，先确定设备的结构特征，确定设备包含多少种类元器件，每一种器件有多少，由此可计算出设备的故障率。设备的故障率是预测备件的必要前提，然后再提供保障概率、保障时间和设备数量来预测备件需求量。这一模块既可用于初始备件需求量的预测，也可用于后续备件需求量的预测。

2）基于统计数据计算备件需求量

装备使用一定时期后，就会发生一定的故障，当故障数据累积到一定数量以后，可以用统计方法分析设备的寿命分布和故障率。确定了设备的寿命分布和故障率以后，我们就可以用相应的备件需求预测模型预测备件的需求量。装备备件保障软件把可靠性的统计计算方法和备件需求预测方法集成到软件中，使用时只须提供装备的故障数据、保障概率、保障时间和设备数量即可预测备件需求量。这种方法需要较多的故障数据，故障数据越准确、越多，统计得出的设备寿命分布越符合实际，预测出的备件需求量越准确。这一方法可用于电子设备备件的需求量预测，也可用于其他类设备备件的需求预测。

6 结论

由于引进装备缺少设计资料，不能完全掌握其性能，无法准确地做好对它的保障工作。在这样的情况下，本文分析了引进装备的可靠性，建立了备件需求预测模型，用引进装备的可靠性特点预测一定时期内对备件的需求量，根据经济订货批量公式的原则制定订货方法，并结合制作的装备备件保障软件，很好地解决了引进装备的保障工作问题。

[1]徐宗昌.保障性工程[M].北京:兵器工业出版社,2002:27-44.

[2]花兴来,刘庆华.装备管理工程[M].北京:国防工业出版社,2002:65-75.

[3]贺国芳.可靠性数据的收集与分析[M].北京:国防工业出版社,1995:49-147.

[4]李宗平,杜文,刘海燕,等.基于可靠性的系统备件储备量设置方法的研究[J].物流技术,2001(2):18-19.

[5]王强,史超,严盛文,等.一种维修备件储备量决策分析模型[J].现代制造工程,2003(5):77-79.

[6]杨翠蓉,尹平林,王明哲,等.企业最优库存控制研究[J].应用科学学报,2002(6):193-196.