基于Markov理论的反舰导弹突防舰载防空火炮效能评估

韩 维，张华宇，岳奎志，史建国

（1.海军航空工程学院 七系，山东 烟台 264001；2.海军专项工程办公室，北京 100085）

反舰导弹对舰艇的攻击是一个复杂的过程。首先，要成功发射反舰导弹；其次，要突防防空导弹的拦截；再次，要突防n座舰载防空火炮的拦截。在两种突防过程中，还伴随着军舰上有源电子干扰和无源电子干扰对反舰导弹制导的影响。所以，作战时1枚反舰导弹成功击中1艘军舰是非常困难的，这就需要探讨m枚反舰导弹同时攻击1艘军舰的“饱和”攻击战术问题，而m枚反舰导弹突防n座防空火炮是反舰导弹攻击军舰的一个重要环节，也是军舰末端防御环节，具有一定的军事研究价值。以往研究突防效能评估模型，常使用概率法、层次分析法、排队论法、蒙特卡罗法等[1-4]，各有优缺点，但这些方法共同存在的不足是缺少动态性，而采用Markov 理论[5-6]就能动态地评估m枚反舰导弹随时间、距离、海况变化情况突防效能，该方法被广泛地应用在作战效能分析的各方面。

1 预备知识

本文所采用的马尔可夫模型是一个在作战模型建模中经常应用的一种随机过程模型。

一个随机过程，如果对于每一时刻 t0，系统未来处于任何状态的概率仅与当时（t=t0）的状态有关，而与系统是怎样和何时进入这种状态无关，这种随机过程为马尔可夫随机过程。

1.1 马尔可夫链

马尔可夫链数学表达式：

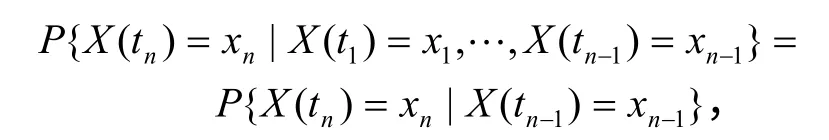
式中：X (ti)=xi表示处于 ti(i=1,2,…,n)时刻的状态。马尔可夫具有的这种性质，称为马氏性，或称为无后效性。

若马尔可夫链X(t)，从t时处于状态i，转移到t+∆t时处于状态j的转移概率与转移的起始时间t 无关，为：

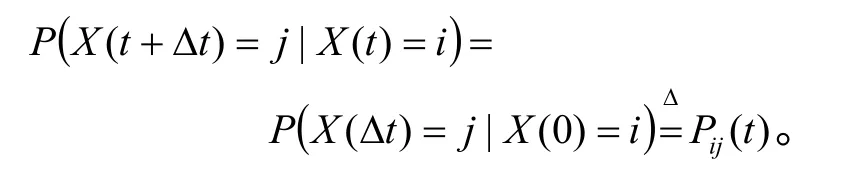
把Pij(t)排成的矩阵 P(∆ t)=[pij(t)]成为马尔可夫链状态概率转移矩阵，在此有：

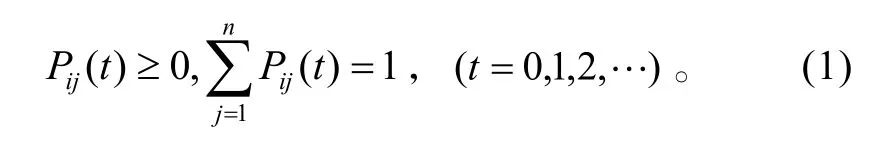
1.2 吸收马尔可夫链

为了研究方便，进行如下假设：①组成系统单元的毁伤率的分布为服从λ指数分布；② X (t)表示系统在时刻t的状态；③ 每个单元无论处于什么状态都是相互独立的。

Pij=1的状态称为吸收状态。若马氏链中至少含有一个吸收状态，并且从每个非吸收状态出发都可以达到某个吸收状态，则称为吸收马氏链。

则X(t)是一个吸收马尔可夫链。假定单元的毁伤率为λ。根据状态转移图1，可写出马尔可夫链状态概率转移的矩阵P(∆t)，即：

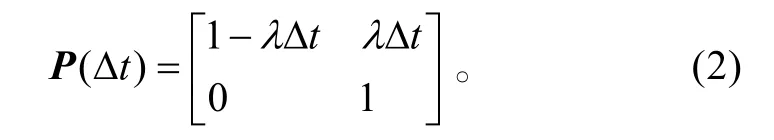
在 ∆t时间内马尔可夫链状态转移方程为：

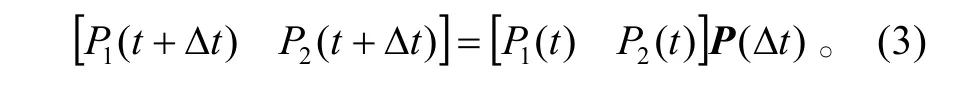
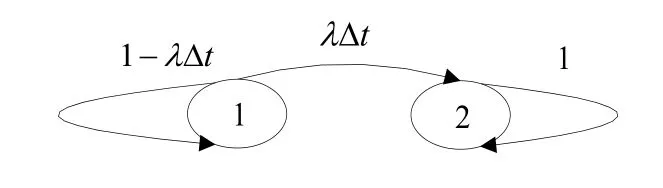
图1 吸收马尔可夫链状态转移图

2 分析模型

2.1 导弹突防防空火炮的Markov模型推导

设反舰导弹初始m枚，其进入带有n座近程防御火炮的军舰射击范围内，λ为反舰导弹被击毁的概率。则反舰导弹突防防空火炮的吸收马尔可夫链状态模型如图2所示，图中 i=m,m −1,…,1,0分别代表在突防过程中有 m,m− 1,…,1,0枚导弹生存；在 ∆t时间段内有n座防空火炮一起射击来袭导弹，反舰导弹的毁伤概率为nλ ∆t；1− nλ ∆t代表该时间段内状态空间为i的反舰导弹的生存概率。

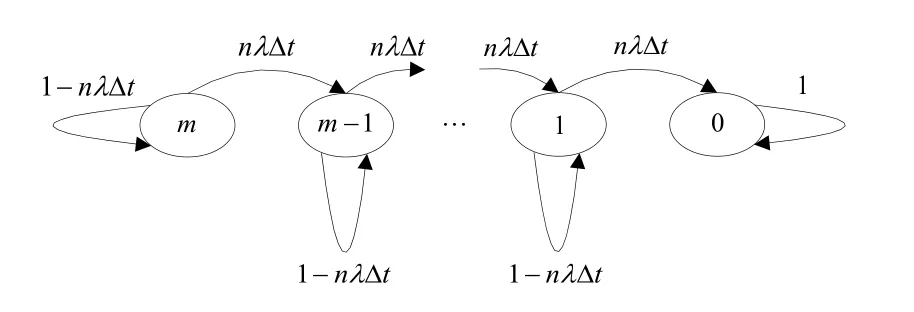
图2 突防防空火炮的吸收马尔可夫链状态转移图

令Pi(t)(i=m,m − 1,…,1,0)表示t时刻状态空间为i的概率。

开始时t=t0，当 t=t0+∆t时导弹突防成功的概率等于导弹在t=t0时没有被击毁的概率Pi(t)，减去n座防空火炮击毁导弹的概率Pi(t)nλ ∆t，即同理可得：

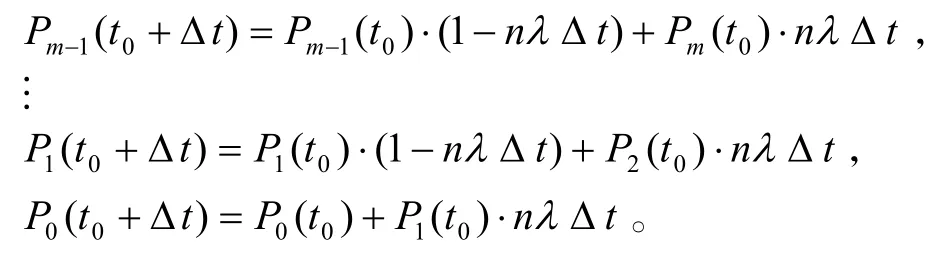
归纳起来，得出不同时间点状态空间中各状态概率：

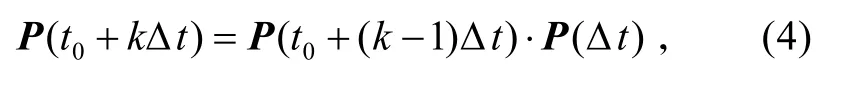
式中：

由式(4)可知，这是一个典型的吸收马尔可夫链模型。

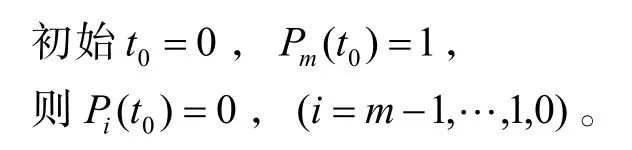
某时刻反舰导弹突防的数目等于各个状态的导弹数目与相对应状态概率的乘积，即：

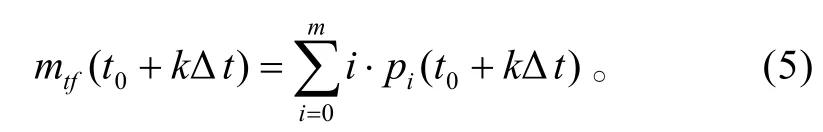
某时刻反舰导弹被击毁的数目为：

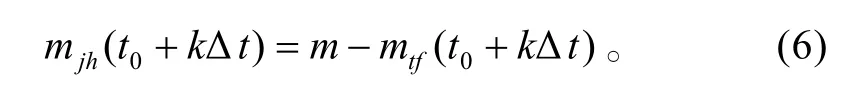
某时刻反舰导弹突防军舰的防空火炮的效率：

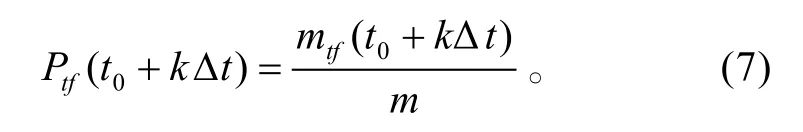
2.2 反舰导弹被火炮击毁概率

反舰导弹被击毁概率λ为：

式中：DP为反舰导弹被探测的发现概率；PH/D为发现后被击中的条件概率；PK/H为弹丸击中反舰导弹后导弹被毁伤的条件概率。

2.3 考虑海况等级下反舰导弹被火炮击中概率

军舰在航行中，海浪会导致舰体纵摇、横摇、垂荡等运动，严重影响舰上防空火炮的射击精度。舰船的倾斜和摇摆环境除了与风浪大小有关外，更重要的与舰船设计的稳定性有关[7]。

在不同海况等级条件下，海浪对舰体摇摆导致防空火炮弹丸的散布角度为

式中：ς为炮弹丸的散布角度（°）；f为射击精度修正系数，一般取0.9；υ为海况等级，作战条件下，海况等级取1～5。

防空火炮发射的密集弹丸分布是一个圆锥形区域，如图3所示。

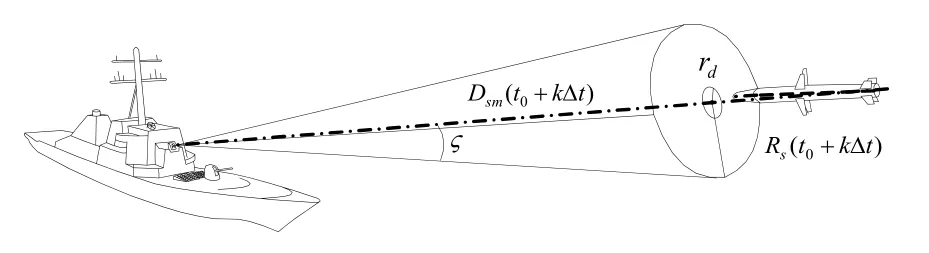
图3 防空炮弹射击空间示意图

设反舰导弹超低空匀速飞向军舰，导弹有效被攻击截面积可视为半径为rd的圆形，并且导弹以匀速 vdd飞向目标，军舰上每座防空火炮的射速为ρk，弹丸的散布角度为ς，设弹丸服从均匀分布，防空火炮最大有效射击距离为Dmax，最小有效射击距离为Dmin。

反舰导弹在 t=t0+k∆t (k=0,1,…,nn)时刻突防军舰的距离为：Ltfm(t0+ k∆t)=vddk∆t。

反舰导弹在 t=t0+k∆t(k=0,1,…,nn)时刻距离军舰的距离为：

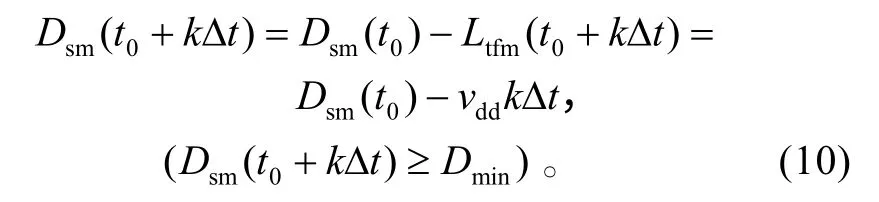
最大时间点nn为：

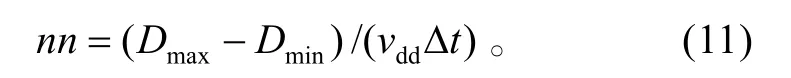
在t=t0+k∆t时刻防空火炮发射的弹丸在距离军舰 Dsm(t0+k∆t)点处的误差半径为：

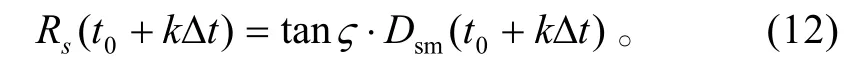
在t=t0+k∆t时刻防空火炮发射的弹丸命中导弹的概率为：

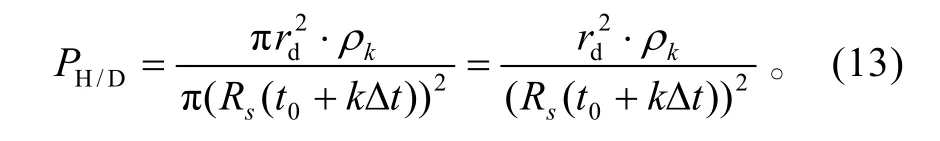
3 仿真实例

设初始时刻 t0=0，Dsm(t0)=4km，X1型反舰导弹速度1 000 m/s，X2型反舰导弹速度300 m/s，防空火炮最小有效射击距离 Dmin=500 m，导弹半径rd=0.18 m，每座防空火炮射速 ρk=75 发/秒（4 500发/分），军舰上有防空火炮座数为n=2，反舰导弹被舰炮命中1 发后其毁伤概率 PK/H=0.5，反舰导弹被探测到的概率 PD=1。则反舰导弹突防军舰近程防空火炮的仿真结果如下。

如图4所示，海况等级越高，导弹突防效率越高；海况等级越低，导弹突防效率越低。当海况等级为1级时，单发X1型反舰导弹到距离军舰500 m止，突防2座防空火炮效率为59.9%；其他条件相同，当海况等级为2级时，X1型导弹突防效率为82.8%，当海况等级为3级时，X1型导弹突防效率为93.3%，当海况等级为4级时，X1型导弹突防效率为97.5%，当海况等级为5级时，X1型导弹突防效率为99.1%。由此可知，海浪对舰船摇摆直接影响军舰上防空火炮的射击精度。

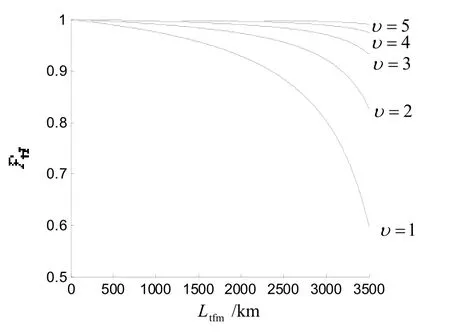
图4 不同海况等级条件下单发X1型反舰导弹突防军舰上2座防空火炮的效率

如图5所示，反舰导弹速度越快，导弹突防效率越高。当海况等级为1级时，单发X1型反舰导弹到距离军舰500 m 止，突防2座防空火炮效率为59.9%，单发X2型反舰导弹到距离军舰500 m 止，突防2座防空火炮效率为18.1%。由此可知，超音速反舰导弹比亚音速反舰导弹突防效率高。

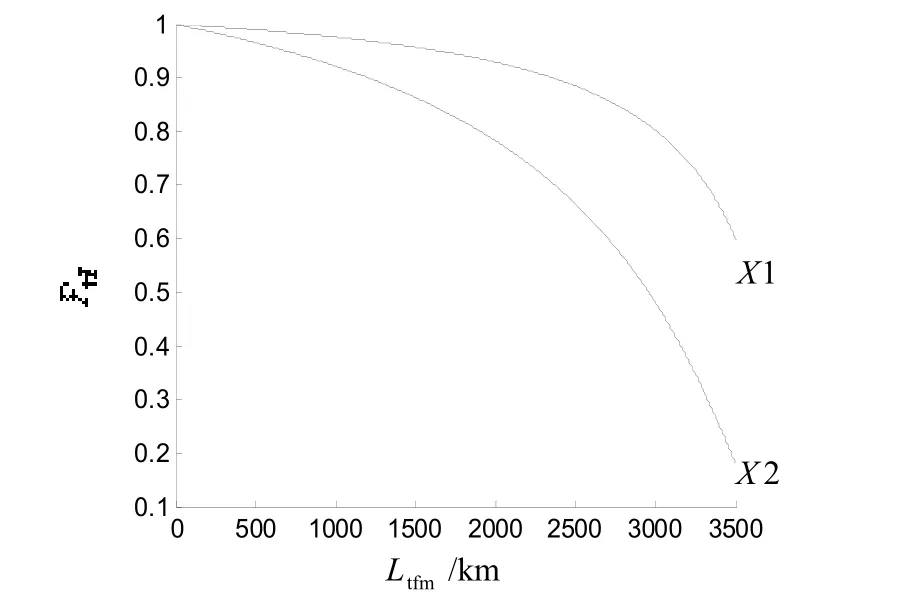
图5 在1级海况等级条件下单发X1、X2型反舰导弹突防军舰上2座防空火炮效率

从图6、7可知，导弹突防防空火炮效率随反舰导弹枚数不同而不同。X2型反舰导弹为1枚时，突防效率为18.1%；X2型反舰导弹为2枚时，突防效率为33.5%；X2型反舰导弹为3枚时，突防效率为47.5%；X2型反舰导弹为4枚时，突防效率为58.3%；X2型反舰导弹为5枚时，突防效率为66.0%。由此可知，反舰导弹数量越多，突防防空火炮效率高。

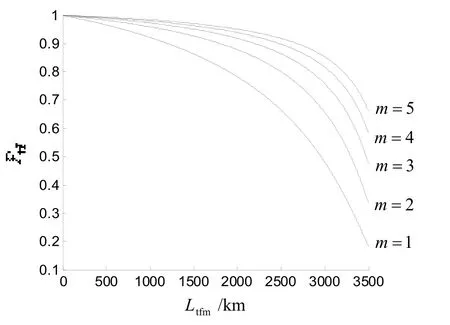
图6 在1级海况条件下m枚X2型反舰导弹突防军舰上2座防空火炮效率

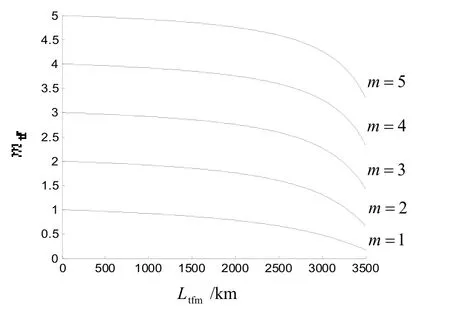
图7 在1级海况条件下m枚X2型反舰导弹突防军舰上2座防空火炮突防枚数

在保证有2枚反舰导弹成功突防带有2座防空火炮的军舰近程防御时（大于90%即可认为成功突防），突防防空火炮刚开始时，需有导弹枚数见表1。

表1 突防防空火炮之初需要导弹枚数

4 结束语

基于Markov 理论反舰导弹突防防空火炮效能评估模型，能够动态地评估不同海况等级条件下，齐射m枚反舰导弹突防军舰n座防空火炮的效能，这对于在攻击水面舰艇作战中，如何根据海况等级不同、舰艇上防空火炮座数不同而采取发射不同型号的导弹枚数用于突防防空火炮的需求具有现实的指导意义。

[1]徐浩军,魏贤智,华玉光,等.作战航空综合体及其效能[M].北京:国防工业出版社,2006:2-17.

[2]ПОПОВ И С.Основы моделирования и системный анализ эффективности авиационных комплексов[M].Москва ВВИА,2002:5-15.

[3]岳奎志,韩维,王庆官.基于排队论的机群出动能力模型[J].海军航空工程学院学报,2009,24(2):224-228.

[4]王斯福,吴晓华,张克,等.基于排队论的飞行器协同突防效能分析[J].战术导弹技术,2007(1):10-15.

[5]许诚,孙永胜,孙锦.基于Markov 过程的反舰导弹突防舰艇编队能力评估[J].飞行力学,2009,27(2):93-96.

[6]岳奎志,侯志强,韩维,等.机群出动能力的Markov模型[J].系统仿真学报,2008,20(22):6278-6282.

[7]中国船舶重工集团公司.海军武器装备与海战场环境概论[M].北京:海洋出版社,2007:467-468.