辨析重力与万有引力的关系
冯海燕
(大庆市大庆实验中学 黑龙江大庆 163316)
重力,是学生在学习高中物理受力分析中是最常用到的一个力.然而很多人对重力的概念却存在着模糊甚至是错误的理解.在学习万有引力一章时,大多数教师都会这样叙述:“地面上的物体,地球施与的万有引力的一个分力提供向心力,万有引力的另一个分力就是重力.”我们知道,力是按照效果分解的,一个分力提供向心力,向心力是效果力,那么重力的效果是什么呢?本文将辨析重力与万有引力的关系.
人教版《物理·必修1》中“重力基本相互作用”一节是这样引入重力概念的:“地面附近的一切物体都受到地球的吸引,由于地球的吸引而使物体受到的力叫做重力.”在学习万有引力之前,可以从新课程渗透式定义的理念上给予这样的概念,即使有不确切的地方,也可以算作一个伏笔,交代学生学过万有引力再作讨论.人教版《物理·必修2》中“万有引力理论的成就”一节指出“若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即由此可解出M=从这之后,很多学生会发出如下几种疑问.
(1)重力的方向指向地心吗?
(2)匀速圆周运动合力提供向心力,为什么物体随地球自转却是万有引力的一个分力提供向心力呢?
(3)“地球自转的影响”到底有多大?其他星体表面也有“万有引力近似等于重力”的说法吗?等等.
笔者认为,要回答好上述问题,在学过万有引力后,就必须对重力的概念进行深化.下面笔者从不同的参考系予以分析.
1 从地球外的惯性系观察
若忽略地球的公转,则地球上的一切物体跟随地球自转而做匀速圆周运动.这样,物体受到的合力提供向心力.从施力物体上分析有地球施与的万有引力F引,还有地面施与的支持力F支,二力矢量和提供向心力F向,如图1所示.支持力属于弹力,它的方向要垂直于接触面的切面.由于地球的自转,以及地球的形状并非正球体,而是两极略扁、赤道略突的椭球体,故物体所在处的切面方向并不垂直于指向地心的方向(除赤道、两极外).即支持力的方向一般并不在物体与地心连线所在的直线上,如图1.人们的经验认为,物体的重力(生活中叫做重量)通过静置于水平面上时受到的支持力体现出来(我们平时称体重就是这个道理),这就是我们平时说的静置于水平面上的物体重力与支持力是一对平衡力.所以重力的方向就自然不指向地心了,这个方向就是我们所说的“竖直向下”的方向;而上述切面方向就是水平方向.
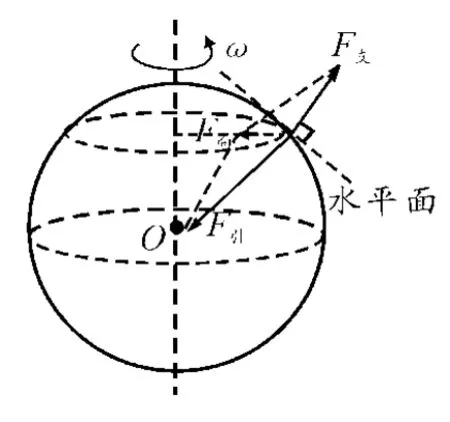
图1
那么,为什么我们能忽略地球的自转而认为地面上物体的重力与地球引力相等呢?以赤道上物体为例.
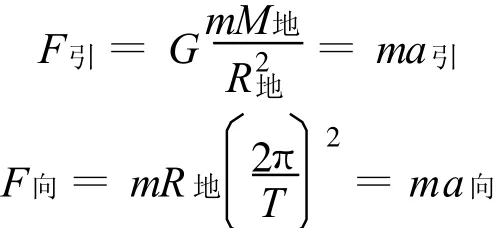
将 G=6.67×10-11N·m2/kg2,M地=5.98×1024kg,R地=6.4×106m,T=24×360 s代入,得a引 =9.8m/s2a向 =0.036m/s2相差近300倍.还可以证明,重力与万有引力方向的最大偏差仅为6分.可见,忽略地球自转是可以的,这种近似是建立在地球自转角速度不是很大的前提下.
但是有些题目却认为无论什么星体表面的物体都有星球的引力等于重力.
【例】(2007年高考四川理综第17题)我国探月的“嫦娥工程”已启动,在不久的将来,我国宇航员将登上月球.假如宇航员在月球上测得摆长为 l的单摆做小振幅振动的周期为T,将月球视为密度均匀、半径为r的球体,则月球的密度为

解析:由单摆周期公式
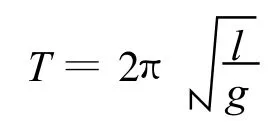
得
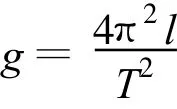
再由牛顿第二定律
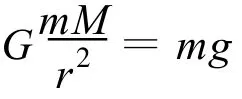
可得
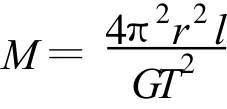
得

故选项B正确.
很明显,本题的解析默认忽略了月球的自转影响,但题目中并未提示考生月球的自转可以忽略不计.这种默认在星体自转过快时并不成立.
在教学中,多数教师把万有引力与重力、向心力的关系画成图2所示情形,并将其叙述为“地面上的物体,地球施与的万有引力的一个分力提供向心力,万有引力的另一个分力就是重力”如开篇所引.
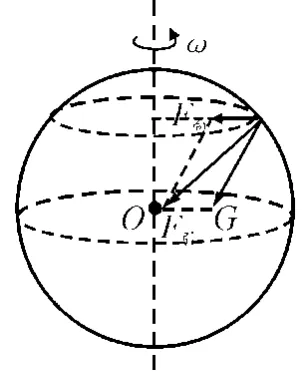
图2
可以说,重力的效果是使地面上的物体压紧地面,或者使空中的物体落向地面.或者说重力是人们的一种感觉、一种经验.这种说法对理解超重现象和失重现象很有帮助.比如人乘电梯加速上升时
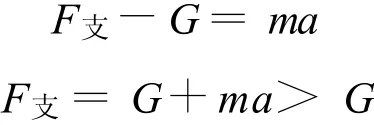
人们的经验依然认为重力等于支持力,就发生了超重现象.
2 以地球为参考系(非惯性系)
物体在万有引力、惯性离心力和支持力三个力的作用下相对地面静止.把物体所受的万有引力和惯性离心力的合力作为重力,如图3所示,于是我们在平时受力分析时就只说“物体的支持力与重力平衡”了(当物体运动时,还应考虑科里奥利力的影响.这个影响较小,通常可以不计).当然,中学阶段并不要求非惯性系下的受力分析,在考虑地面物体运动时,由于惯性离心力相对较小,所以还是近似地把地面参考系作为惯性系.
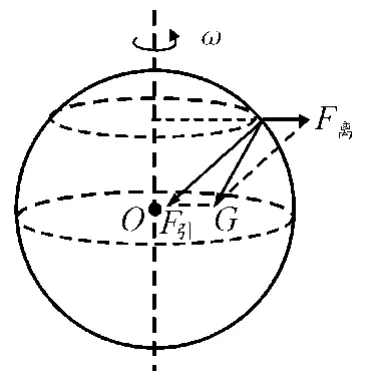
图3
重力和万有引力的关系,是学生最难辨清的关系之一,如何让学生在现有知识水平范围内充分理解,还需继续探讨.

