利用分解和微元法求复场中曲线运动的最远距离
刘月荣
(邗江中学 江苏扬州 225009)
运动的合成与分解是研究复杂运动的重要方法.在研究比较复杂的运动时,常常采用分解的方法,将运动看作是两个或几个比较简单的运动组成的,使问题容易解决.在应用分解的方法时要注意“运动的独立性原理”.这是物体运动的一个重要特性,即一个物体同时参与几种运动,各分运动都可看作是独立进行的,它们互不影响.
“微元法”是分析连续过程积累的一种分析方法,其精髓就是把确定的研究对象分割为无限多个无限小的部分,然后抽取其中一部分加以研究,从而认识整体或全过程的性质和规律.这实质上是“从复合到单一,从单一到复合”的分析与综合思维方法.
在高三专题复习中常遇到复合场中的最远距离的求解,即可利用分解的方法和微元法来加以分析.
【例1】如图1所示,在空间有相互垂直的匀强电场E和匀强磁场B,一电子从原点释放,求电子在y轴方向前进的最大距离.(不计电子重力,已知电子电荷为e,质量为m)

图1
分析:对电子在任一位置的受力进行分析,电子受到竖直向上的电场力eE及与速度垂直的洛伦兹力Bev.将电子的速度分解为水平方向的速度vx和竖直方向的速度vy,同时将洛伦兹力也分解为水平方向的作用力和竖直方向的作用力.而水平方向的洛伦兹力是由于竖直方向的速度产生的,竖直方向的洛伦兹力是由于水平方向的速度产生的,因此水平方向的洛伦兹力为Bevy,而竖直方向的洛伦兹力为Bevx(图2).
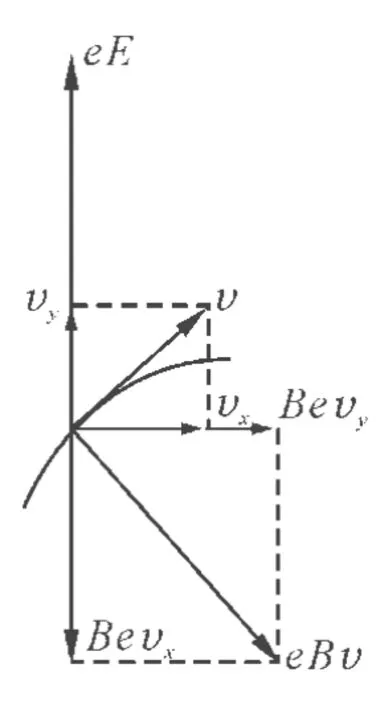
图2
由牛顿第二定律得

设电子到达最高点时的速度为v,即
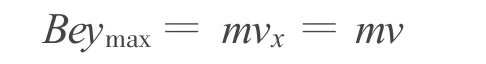
全过程中只有电场力做功,根据动能定理得
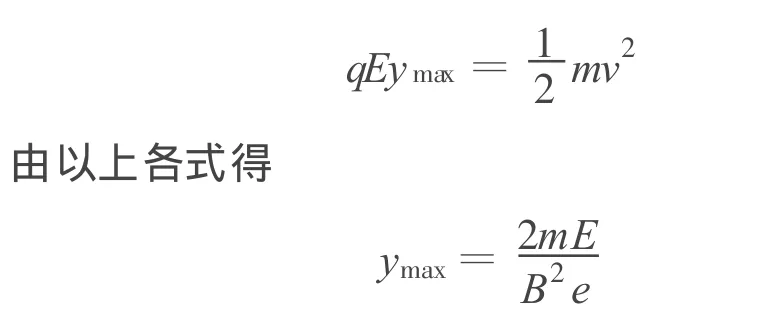
【例2】在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴和y轴建立直角平面坐标系.一质量为m、带电荷为+q的微粒从点由静止释放后沿直线 PQ运动(图3).当微粒到达Q(0,-l)的瞬间,撤去电场,同时加上一个垂直于纸面向外的匀强磁场(图3中未画),磁感应强度的大小,该磁场有理想的下边界,其他方向范围无限大.已知重力加速度为g.求:
(1)匀强电场的大小;
(2)撤去电场加上磁场的瞬间,粒子所受合外力的大小和方向;
(3)欲使微粒不从磁场下边界穿出,该磁场下边界的y轴坐标应满足的条件.
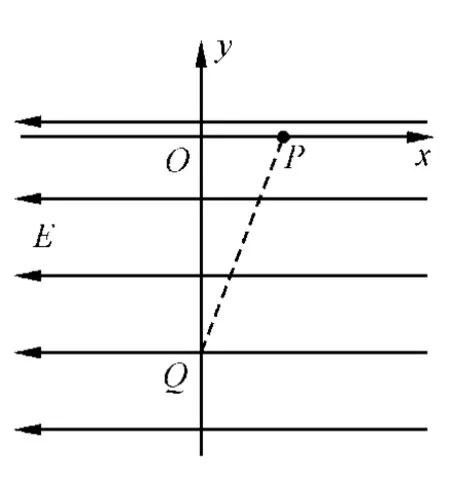
图3
分析:(1)微粒沿PQ直线运动时受水平向左的电场力和竖直向下的重力作用,合力沿PQ方向.因此
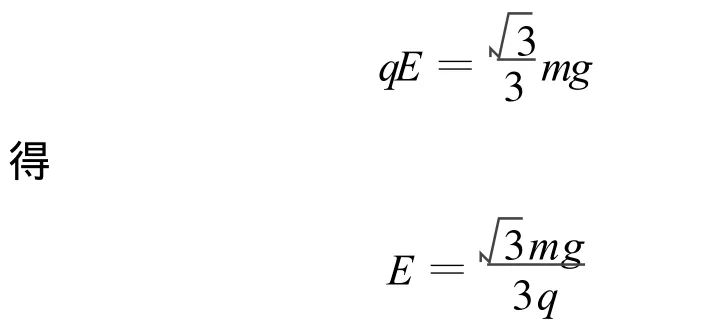
(2)撤去电场,加上磁场的瞬间,粒子在竖直方向的速度为

当微粒运动到任一点时,将微粒的速度分解为水平方向的vx和竖直方向的vy,同时将洛伦兹力也分解为水平方向的作用力和竖直方向的作用力.而水平方向的洛伦兹力是由于竖直方向的速度产生的,故为Bqvy;竖直方向的洛伦兹力是由于水平方向的速度产生的,故为 Bqvx(图4).于是有
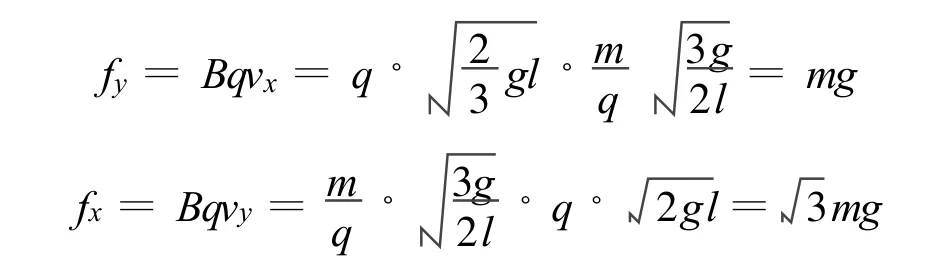
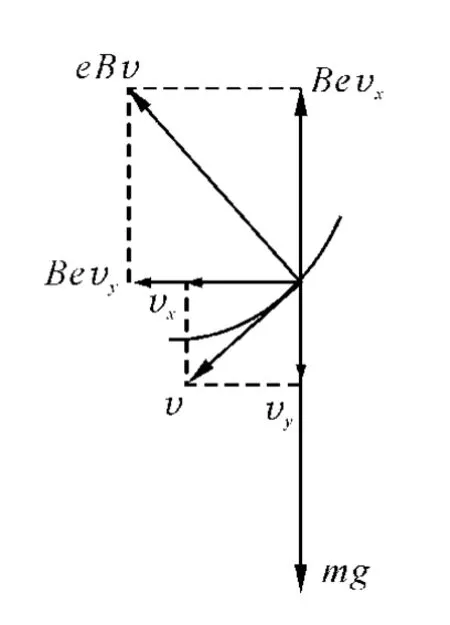
图4
(3)撤去电场,加上磁场后,微粒做曲线运动.由牛顿第二定律得

其中v为微粒运动到磁场最远点的速度,vx为Q点的水平速度

以上是带电粒子在复合场中做曲线运动的典型例题.对于曲线运动,一般采用分解的方法处理问题;而利用运动的分解和微元法求曲线运动中的最远距离,正是这种题型中的亮点,也能考查学生的独创能力.

