非均匀水平应力场中井壁结构的优化设计研究

牛少卿，杨双锁，王志刚，寇永嘉

(太原理工大学矿业工程学院，山西太原030024)

1 引言

立井是矿山生产运输的咽喉要道,立井的施工是矿山建设十分重要的一环,作为立井永久支护的井壁结构——井筒,其稳定性状况直接影响到矿山的安全生产,因而井筒的受力和变形情况是值得关注的[1-3]．

由于地质构造、岩体自身的特性以及施工等方面的原因,井筒所处的水平应力场并非均匀分布．传统井壁是一种等厚度圆筒结构物,根据弹性理论可知,在均匀应力场中井壁上所受的应力和产生的变形呈均匀分布;而在非均匀应力场中,井筒所受的应力和产生的变形呈现不均匀分布状态，这种不均匀性对等厚度井壁结构的稳定性是不利的,因此寻找非均匀水平应力场中井壁的合理结构具有积极的意义．

随着计算机应用技术的提高，以有限元分析技术为基础的形状优化技术得到了发展[4]．它主要研究如何确定连续体结构的边界形状或者内部几何形状，以改善结构的特性，其中更多的是降低应力集中、改善应力的分布状况、提高稳定性、延长结构寿命[5-6]．它通过改变区域的几何形状来达到某种意义上的最优．因此利用常规设计手段完成井壁结构的整体尺寸设计后，再利用形状优化技术对井壁的局部边界形状进行优化，使得井壁的结构在主体结构上满足设计准则的要求，在局部区城又改善了应力分布．同时通过形状优化不仅可以降低应力集中，更重要的是提高了井壁材料的利用率,使载荷能够均匀分布在井壁结构上．

形状优化是建立在结构应力分析技术上的，在结构应力分析过程中,成熟的分析方法是:有限单元法．由于其目标函数与设计变量之间大多为隐式函数关系，因此对目标函数的求导计算即敏感性分析是形状优化过程中的一个难点.另一难点是目标函数与设计变量之间是一种非线性关系，有时其非线性程度还很高．要将形状优化技术应用于工程的常规设计过程中，就必须要解决这两个问题．所幸的是，随着计算机分析技术和应用技术的发展，人们对形状优化问题开展了大量的研究，这两个难点问题都得到了部分解决．现在许多商业有限元软件都能完成部分形状优化的分析计算，因此将形状优化应用于常规设计中已成为未来矿井设计的发展趋势．

本文提出了一种新型的井筒结构模型，利用有限元软件的优化设计模块对其进行形状优化设计，得出了井壁结构的合理参数．

2 计算模型

摩尔-库仑准则体现了岩土材料压剪破坏的实质，所以获得了广泛的应用．但这类准则没有反映中间主应力的影响，不能解释岩土材料在静水压力下也能屈服或破坏的现象．德鲁克-普拉格准则是在摩尔—库仑准则和塑性力学中著名的米赛斯准则基础上的发展和改进[7-10]．本文对岩石材料采用德鲁克—普拉格弹塑性结构模型模拟：

其中 I1=σ1+σ2+σ3=σx+σy+σz′，为应力张量第一不变量；

为偏应力张量第二不变量；

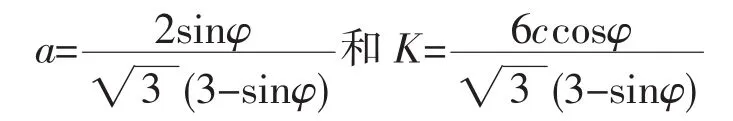
此处a和K均为常数，c和φ分别为材料的黏结力和摩擦角．

德鲁克—普拉格准则计入了中间主应力的影响，即考虑了静水压力的作用，克服了摩尔-库仑准则的主要弱点．已在国内外岩土力学与工程的数值计算分析中获得广泛的应用．

本文运用数值模拟分析技术，对不均匀侧压力下井筒结构进行优化，采用德鲁克—普拉格弹塑性模型进行计算．计算模型长40 m，宽40 m，井筒半径4.1 m，模型侧边界距井筒中心约为井筒半径的10倍．模型边界条件为：左边界水平方向0位移约束，下边界垂直方向0位移约束，模型上边界分别施加10、11、12、13、14、15 MPa的均布压力，右边界施加10 MPa的均布压力．优化过程中，井壁内壁为圆形，外壁为椭圆形，上部井壁厚度保持0.6 m，右边井壁厚度从0.6 m开始增大．优化分析整体模型见图1;计算参数见表1．

计算中井筒断面外壁长轴c与短轴b之比A为设计变量．合理优化中，内壁最大环向应力和最小环向应力差与最小环向应力之比为状态变量，状态变量小于(q1-q2)/q2，椭圆长轴长度c为目标函数；均匀优化中，模型中井壁内壁环向应力的方差NSY_DY为目标函数．A的取值范围为1～5．

图1 优化分析整体模型图

其中 q1分别为 10、11、12、13、14、15 MPa,q2为 10 MPa．

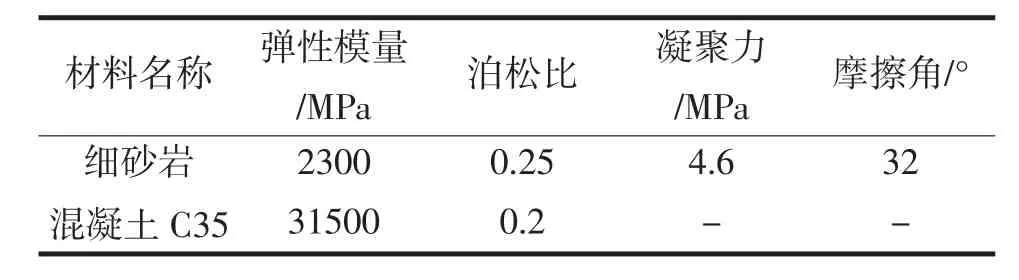
表1 模型材料力学参数

3 计算结果

经过有限元软件优化模块的优化，可以得到不同侧压条件下井壁设计变量与目标函数的关系以及不同侧压条件下不同优化设计变量A值相关的井壁参数．以上述变量A来进行优化的结果见下列图表所示．

图2为不同侧压条件下目标函数NSY_DY与设计变量A的关系曲线．从图中可以看出，A在1～5之间，目标函数NSY_DY存在唯一的极小值点，这个极小值点也就是内壁环向应力分布最均匀的点．不同侧压条件下目标函数的最小值的A点是不同的，随着最大侧压力的增大，目标函数最小值的A点在不断增大，这表明，随着侧压力的增大，井壁外壁椭圆长轴与短轴之比越来越大，即最大壁厚在不断增大．从图中可知，目标函数在达到最小值前，变化速度很小，这就要求合理优化，使得应力分布比较均匀，满足井筒稳定性要求，且所用材料最少．在合理优化中，选取目标函数为井壁外壁椭圆长轴，目标函数与设计变量为线性关系，内壁最大环向应力和最小环向应力差与最小环向应力之比为状态变量，状态变量小于 (q1-q2)/q2，从而使应力沿井壁内壁分布比较均匀，且节省材料．

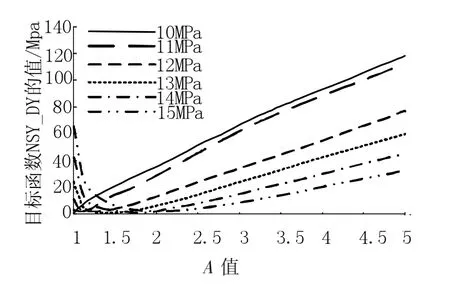
图2 不同侧压条件下目标函数NSY_DY与设计变量A的关系曲线

图3 最大侧压力为15MPa时优化后的井筒内壁环向应力与等厚井筒内壁环向应力对比图

图3为最大侧压力为15 MPa时，优化后的井筒内壁环向应力与等厚井筒内壁环向应力对比图.S为弧AB．从图中可以清楚地看出，在不均匀侧压力下，井筒经过优化后，内壁环向应力分布都得到了明显改善，沿井筒内壁分布比原来均匀了很多，最大环向应力和平均环向应力也得到了较大的减小，这对井筒的稳定性非常有益．

图4 合理优化设计变量A随最大侧压力变化曲线

图5 均匀优化设计变量A值随最大侧压力变化曲线

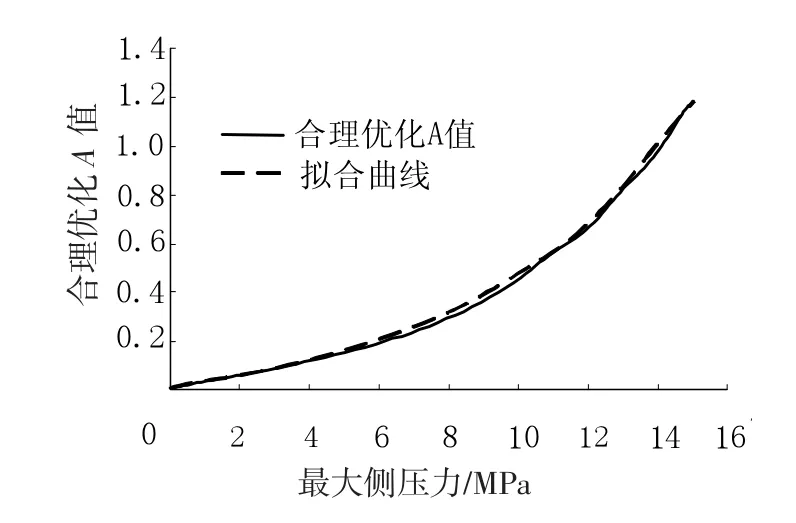
图6 合理优化设计变量A值随最大侧压力变化曲线拟合图

表2 优化后的井筒参数

表3 拟合公式所产生A值与合理优化A值对比列表

表2给出了优化后设计变量A、井壁椭圆长轴、最大壁厚和最大最小壁厚比．图4给出了合理优化设计变量A随最大侧压力变化曲线，图5给出了均匀优化设计变量A随最大侧压力变化曲线．从表2、图4、5中可看出，随着最大侧压力q1的增大，A的值越来越大，椭圆长轴越来越长，井壁壁厚处的厚度越来越大，最大、最小壁厚比也越来越大．

对合理优化设计变量A随最大侧压力变化曲线进行拟合后得到图6，拟合公式为A=Ke-x/t+C，其中K为 1.80297e-4，t为-1.9709，C为0.97397．表3给出了拟合公式所产生A值与合理优化A值对比列表．

4 结论

通过对不同侧压力下井筒井壁合理结构的优化分析得出如下结论：

1)非均匀水平应力场中，等厚度的圆形井筒内壁应力分布并非均匀，不利于井筒稳定性的保持．

2)不同侧压条件下，采用外壁为椭圆内壁为圆的井壁结构能取得较好的效果．

3)在外壁从圆形向椭圆形过渡中存在一个最优处，偏离最优处两端越远应力分布越不均匀，这个最优状态就是井壁应力分布状态最均匀的状态．

4)在井壁应力分布最均匀的状态下，井壁的变形、应力分布合理，对保障井筒的稳定性起到了重要作用．

5)在水平双向原岩应力分别为10 MPa和10～15 MPa的细砂岩中以C35混凝土井壁结构为例得出：合理优化设计变量A和最大侧向压力的关系式为：A=Ke-x/t+C．

[1]张国鑫.钢板-钢筋混凝土复合井壁结构在不均匀侧压力作用下的应力[J].建井技术,1995(5):34-39.

[2]胡学文.井筒在不均匀侧压力作用下的应力[J].安徽理工大学学报:自然科学版,1982,2(2):41-49.

[3]姚直书,孙文若.不均匀侧压力下冻结井筒混凝土井壁结构试验研究[J].阜新矿业学院学报:自然科学版,1995,14(3):30-33.

[4]Hsu Yehaliang.Review of structure shape optimization[J].Computer in Industry,1994,25(1):3-13.

[5]顾元宪,程耿东.结构形状优化设计数值方法的研究与应用[J].计算力学及其应用,1993(3):321-335.

[6]朱灯林.结构拓扑优化设计的研究现状及其应用[J].机械制造与自动化,2005,34(6):7-1l.

[7]Hudson J A，Harrison J P.ENGINEERING ROCK MECHANICS[M].London:Pergamon Press,1997.

[8]殷有泉.非线性有限元基础[M].北京：北京大学出版社,2007.

[9]王建军.岩石破坏德鲁克—普拉格准则的探讨[J].建筑与工程，2009(7):294.

[10]杨桂通.弹塑性力学引论[M].北京：清华大学出版社,2003.