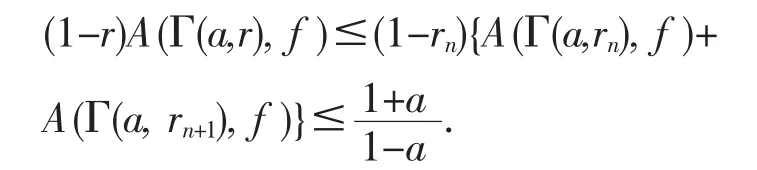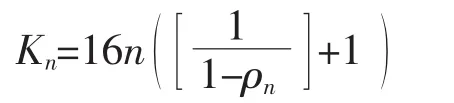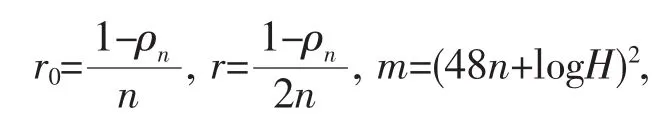单位圆内高阶齐次线性微分方程解的复振荡
金 瑾
(毕节学院数学系,贵州毕节551700)
1 定义
假设熟悉单位圆 Δ={z∶|z|<1} 和全平面 C 上亚纯函数的Nevanlinna值分布理论的基本结果[1-18],采用单位圆上的Nevanlinna理论研究单位圆上的一类高阶高阶齐次线性微分方程的解析性质并得到进一步的结果.本文采用m(r,f),N(r,f),T(r,f)等Nevanlinna理论的标准符号[3,5,6,11].
定义1[4]单位圆Δ内的亚纯函数f(z)的级定义为
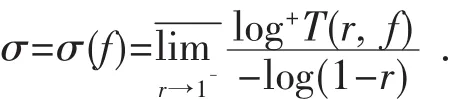
对于单位圆Δ内的解析函数f(z),定义
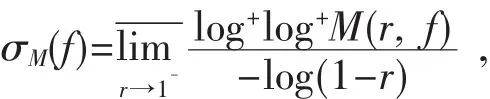
其中M(r,f)是f(z)在单位圆Δ内的最大模.
定义2单位圆Δ内的亚纯函数f(z)的超级定义为

定义3对单位圆Δ内的亚纯函数f(z),如果
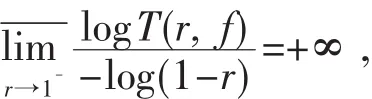
则称单位圆Δ内的亚纯函数f(z)为可允许的.
定义 4 对于圆盘 U(R)={z∶|z|<R}内的亚纯函数f(z),我们定义
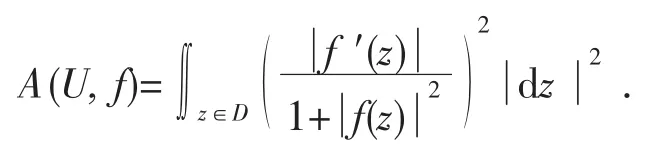
如果U=U(r)=Δ时,记为A(r,f).
2 证明定理所需的引理
引理 1 设 f(z)是单位圆盘 Δ={z∶|z|<1}内的亚纯函数,并且ρM(f)=ρ<∞,则对∀ε>0,存在集合
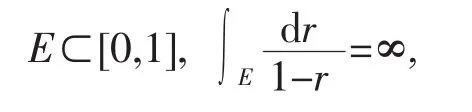
使得对∀r∈E有
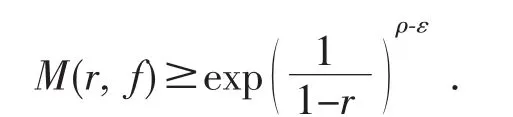
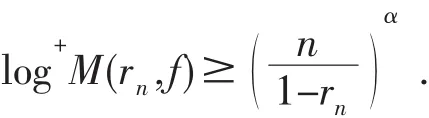
令
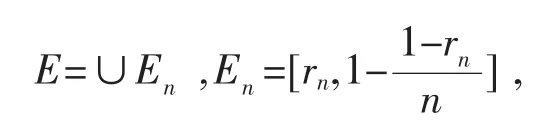
如果 r∈E,则
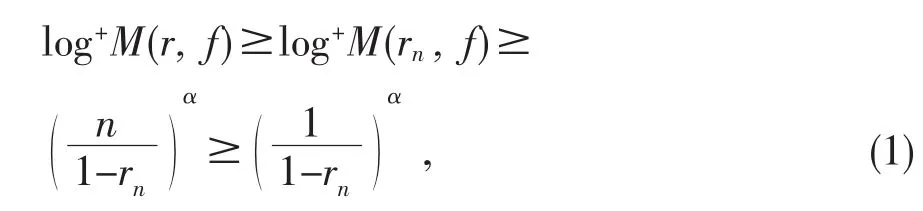
并且
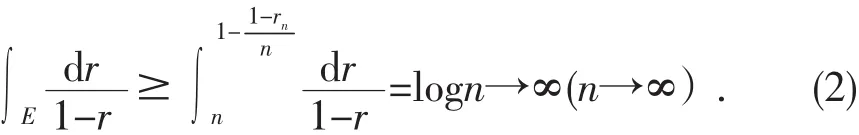
所以由(1)和(2)式可知引理1成立.
引理2设f(z)是单位圆Δ内可允许的亚纯解析函数,ε>0,k,j是满足 k>j≥0 的整数.则至多除去一r值集
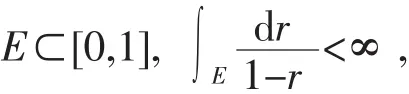
使得对∀z∈Δ,|z|∉E 有

其中C为正常数.
证明 根据文献[18]的引理 5.1.5 及定理 5.1 的证明可知,存在一个常数C1∈(0,+∞)和一个r值集

使得对∀z∈Δ, |z|=r∉E,有

其中

显然s1(r)<s(r)<r,又因为f(z)是单位圆盘Δ内可允许的亚纯解析函数,故由(3)式可得
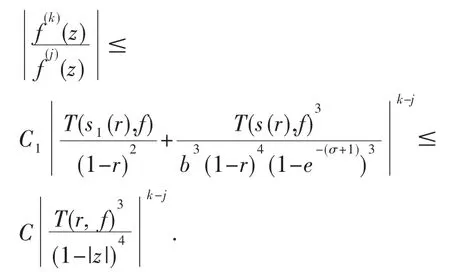
引理 3 设 f(z)是圆盘 U(R)(z∶|z|<R<+∞)内的亚纯函数,a1,a2,a3是复球面上三个两两不同的数,若f(z)在圆盘 U(R)内取值 a1,a2,a3的次数(不计重数)分别为n1,n2,n3.
则 A(r,f)<n1+n2+n3+
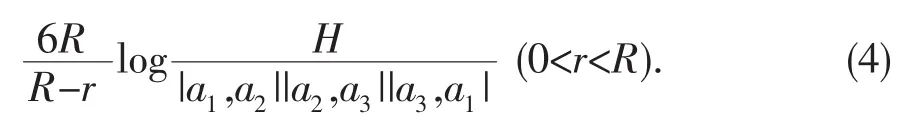
其中H为一个正绝对常数.
证明(1)当a1,a2,a3中没有一个为零或∞时.
① |a1|,|a2|,|a3|中有两个不超过 1 时.不失一般性,设|a1|≤1,|a2|≤1,|a3-a2|≤|a3-a1|.
再设
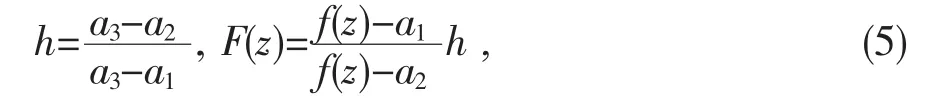
则|h|≤1,且 F(z)在圆盘 U(R)内取值 0,1,∞ 的次数分别为 n1,n2,n3(不计重数).从(5)可知
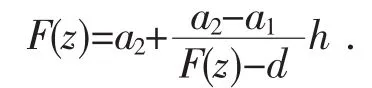
因此对任意的 r和 ρ(0<r<ρ<R)有
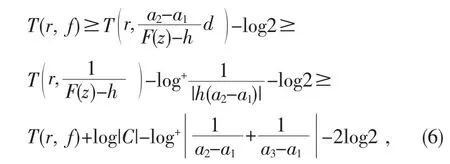
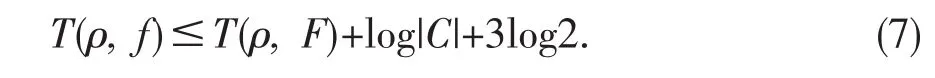
又
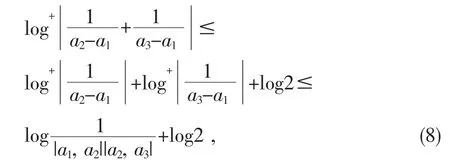
故由(6)(7)和(8)式可得
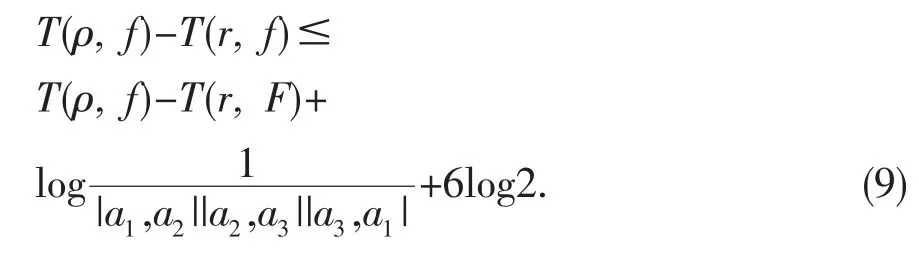
设 T0(r,f)为 f(z)的 Ahlfors-Shimizu特征函数.
则
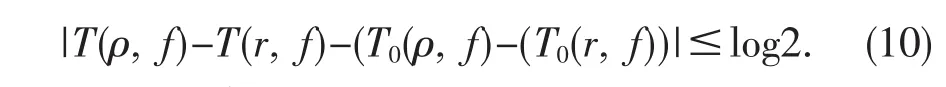
由(9)和(10)可得

因此
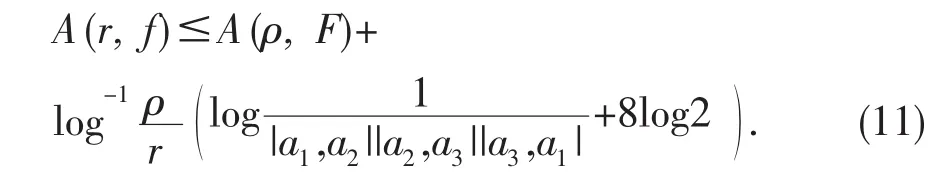
由Ahfors不等式[17]可知
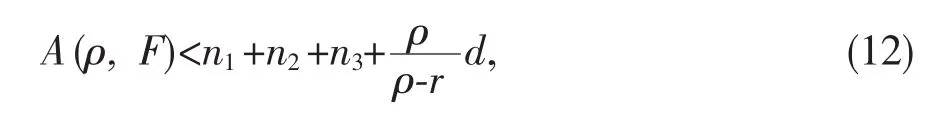
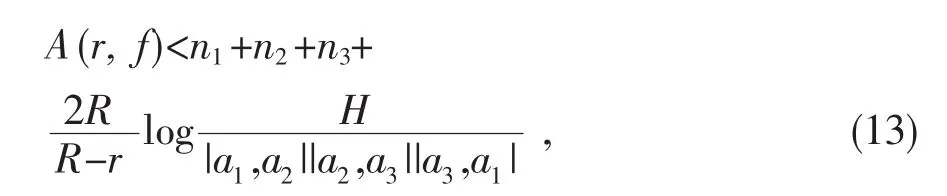
其中 H=28ed.
② (1)|a1|,|a2|,|a3|中有两个大于 1.不失一般性,设|a1|>1,|a2|>1.再设和类似于(1)的论证可得,如果把f(z)和ai(i=1,2,3)用f1(z)和bi(i=1,2,3)来代替,仍然可得到
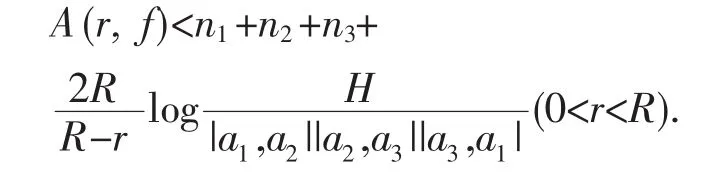
(2)当a1,a2,a3中有一个为∞时.不失一般性,假设|a1|≤|a2|,a3=∞.再设则有f(z)=类似于(6)(7)(9)的证明可得

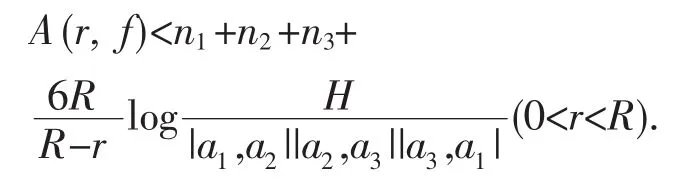
其中H=28ed,d为一个正绝对常数.
(3)a1,a2,a3都是有穷复数时,且有一个为零时.不失一般性,假设a3=0.再设和类似于(二)的论证可得

其中H=28ed,d为一个正绝对常数.
综上所述引理3成立.
引理 4 设 f(z)是圆盘 U(R)={(z∶|z|<R}内的亚纯函数,若存在一个 r0(0<r0<R),使得 A(r0,f)>m≥2,那么对任意使得m≥4(7r-r0)(logH+1)/(r-r0)的r,圆盘{(z∶|z|<r}为 f(z)的以(r-r0)m/4(7r-r0)-logH 为指数的充满圆(其中H为大于1的正常数).
证明 若存在一个 r(0<r<R),使得 U(r)={z∶|z|<r}不是 f(z)以

为指数的充满圆.其中H为引理3中的正绝对常数.则存在复数a1,a2,a3,他们间的球面距离超过e-m,f(z)在圆盘 U(r)={z∶|z|<r}中取这些值至多 d 次.由引理3可知
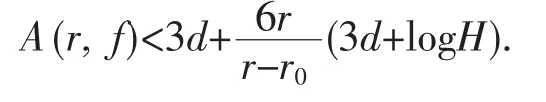
又由于 A(r,f)>A(r0,f)>m,故
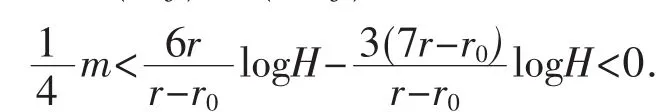
这与m≥2矛盾.因此引理4成立.
3 定理及其证明
定理 设Aj(z)(j=1,2,…,n-1)在 Δ 内解析,且σ0=max{ρM(Aj),j=1,2,…,k-1}<ρM(A0).
则微分方程
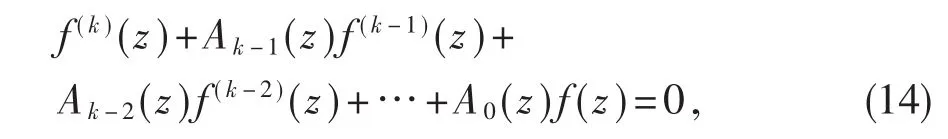
的不恒等于零的解f(z)满足

进一步,若f(z)是微分方程(14)在单位圆盘Δ内可允许的亚纯解,则在单位圆盘Δ内存在一个点列{zn},使得每个圆盘
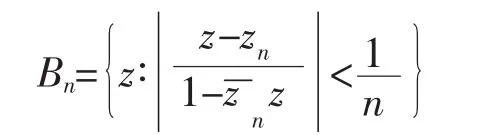
证明 设实数 α 和β满足 σ0<α<β<ρM(A0),如果f(z)是微分方程(14)的不恒等于零的解,则有

由引理2可知,存在一个r值集
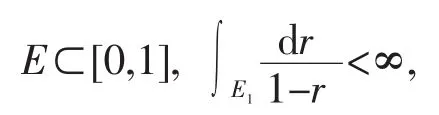
使得对∀z∈Δ, |z|∉E1有
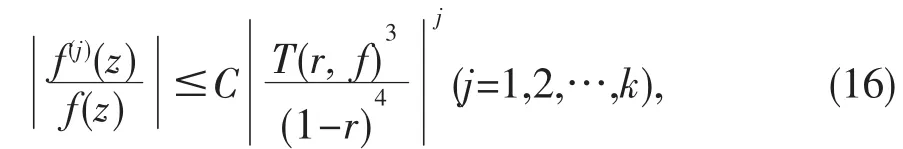
其中C为正常数.
又由引理1可知,存在一对数测度为无穷的r值集 E2,使得对∀r∈E2, |z|∉E1,有
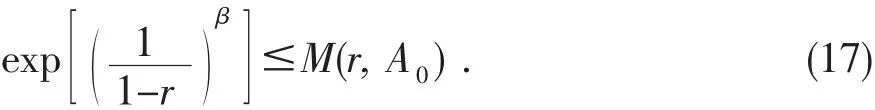
将(16)式和(17)式代入(15)式可得:存在一对数测度为无穷的r值集E⊂[0,1],使得当r∈E,且r→1-时有
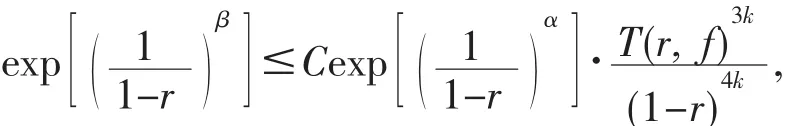
即

从而可得

由β的任意性可知
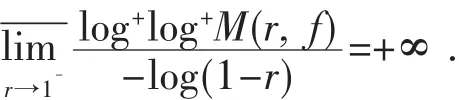
进一步,若f(z)是微分方程(14)在单位圆盘Δ内可允许的亚纯解,则

即
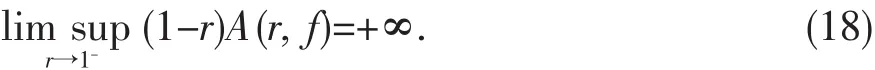
设
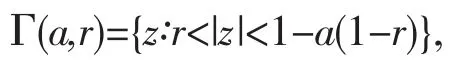
则对∀a∈(0,1)有

否则,存在正数M和a∈(0,1),使得

则有
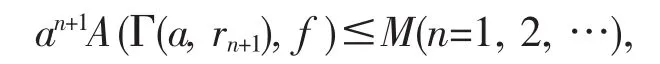
其中rn=1-an及rn+1=1-a(1-rn).
故
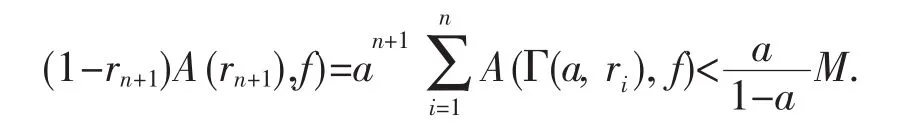
对∀r∈(0,1),存在一个n,使得rn≤r 这与(18)式矛盾,故(19)式成立. 其中H是引理3中的绝对常数. 将 Γ(an,ρn)分成 个区域Dnj(j=1,2,…,Kn),这里 从(20)式至少可得一个j0(1≤j0≤Kn),使得 但 其中 为指数的充满圆. [1]Heittokangas J,Korhonen R,Ra¨ttya¨J.Growth estimates for solutions of linear complex differential equations[J].Ann Acad Sci emm Math,2004,29:233-246. [2]Chyzhykov I,Gundersen G,Heittokangas J.Linear differential equations and logarithmic derivative estimates[J].Proc London Math Soc,2003,86:735-754. [3]Hayman W.Meromorphic Functions[M].Oxford:Clarendon Press,1964. [4]Heittokangas J.On complex differential equations in the unit disc[J].Ann Acad Sci Fenn Math Diss,2000,122:1-54. [5]Tsuji M.Potential Theory in Modern Function Theory[M].New York:Chelsea,1975. [6]Yang Lo.Value Distribution Theory[M].Berlin:Springer-Verlag,and Beijing:Science Press,1993. [7]Chen Zongxuan,Shon Kwang-ho.The growth of solutions of differential equations with coefficients of small growth in the disc[J].J Math Anal Appl,2004,297:285-304. [8]Gundersen G G.Finite order solutions of second order linear differential equa-tions[J].Trans Amer Math Soc,1988,305:415-429. [9]Kwon Ki-ho.On the growth of entire functions satisfying second order linear differential equations[J].Bull Korean Math Soc,1996,33(3):487-496. [10]Chen zongxuan,Yang Chungchun.Some futher results on the zeros and growths of entire solutions of second order linear differential equations[J].Kodai Math J,1999,22:273-285. [11]Yi Hongxun,Yang Chungchun.Uniqueness Theory of Meromorphic Functions[M].Kluwer:Science Press,2003. [12]Cao Tingbin,Yi hongxun.The growth of linear differential equations with coefficients of iterated order in the unit disc[J].Math Anal Appl,2006,319:279-294. [13]Cao tingbin,Yihongxun.On the complex oscillation of second order linear diff-erential equations withanalytic coefficients in the unit disc[J].Chinese Annals of Mathematics(A),2007,28A(5):719-732. [14]Jin Jin.The fix point of solutions and the derivatives of Solutions of higher order entire function coefficients linear differential equations[J].Journal of Mathematical Research&Exposition,2007,27(4):803-813.(in Chinese) [15]Jin Jin.The fixed point of two order derivatives of Solutions of higher order linear differentIal Equa-tions[J].Mathematical Theory and Applications,2007,27(4):107-113.(in Chinese). [16]Jin Jin.The Zero-filling Discs of Solutions of Complex Equation[J].Advances in Mathematics,2005,34(5):609-613.(in Chinese) [17]Tsuji M.Petential theory in modern function theory[M].Tokyo:Maruzen,1959. [18]Heittokanges J.On comples differential equations in the unit disc[J].Ann Acad Sci Fennica Math,Dissertations,2000,122:1-54. Where the coefficients are analytic functions in the unit disc Aj(z)(j=0,1,2,…,k-1),and relations between the growthes of the solution and the coefficeient of higher order homogeneous linear differential equations are given out,and exist of the filling circle alignment of meromorphic permissble solution of higher order homogeneous linear differential equations are proved in the unit disc. Key wods:unit disc;order;filling circle;permissble solution