均衡二部图中一个有限制条件的2－因子

王仲梅，孟献青，

（1．湖南商学院信息学院，湖南长沙 410205；2．山西大同大学数学与计算机科学学院，山西大同 037009）

本文仅考虑简单有限无向图.对度因子的研究是图论的重要分支之一.Dirac[1]证明:若G是一个阶n≥3的图，且最小度，则G为Hamilton图.以此定理为基础引出了多种与度有关的问题的研究，给出了一个不同于文[2]中二部图至少含k个圈的条件.在文中我们有如下记号:

引理1[2]设P=x1x2…xp是G中的一条路，其中x1∈V1，P=2r+d，d=0 或 d=1. 设 y∈V2∩（V（G）－V（P）），如果dp（x1）+dp（xy）≥r+1），则G有一条路P*,使得 V（P*）=V（P）∪｛y｝.

引理2[4]设t＞s是两个正整数，C是G中长为2t的圈，且w∈G－V（C）.如果则C+w包含一个圈C*，使得2s≤l（C*）＜2t.

引理3[4]设s≥3是一个正整数，C是G中长为2s的圈.设

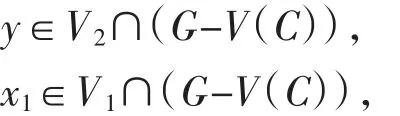
如果dC（x）+dC（y）≥2s－1，则C中存在两个顶点u∈V1和v∈V2，使得C－u+x包含一个长为2s的圈，且uy∈E（G）以及C－v+y包含一个长为2s的圈，且vx∈E（G）.

引理4[5]设C是G中的一个圈，P是G中的一条uv－路，其中 u∈V1且v∈V2，使得 V（C）∩V（P）=ø.设l（C）=2q，如果dC（u）+dC（v）≥q+1，则G包含一个圈 C*，使得 V（C*）=V（C）∪V（P）．

引理 5 设 s≥3是一个正整数，G=（V1，V2）是一个均衡二部图，满足如果G包含k个顶点不交的长至少为2s的圈，则包含一条Hamilton路.

证明 在G中选择k个顶点不交的长至少为2s的圈 C1，C2，…，Ck．使得中的最长路尽可能的长.令设,如果d=0，则结论显然成立.下面假设 d≥1.

设l（Ci）=2ni，对所有的i∈｛1，2，…，k｝，显然由题设知ni≥s,且．不失一般性，设P=x1x2…xp是G1中的一条最长路，其中x1∈V1，P=2r+δ，δ=0 或 δ=1.

为了证明引理的结果我们用反证法.假设G1中不含 Hamilton 路，从而P＜2d.令 G2=G1－V（P），且u∈G2∩V2.因P是G1中的最长路，由引理1知dp（x1）+dp（u）≤r，又x1∉G2，故dG2（x1）=0.而故dG2（u）≤d－r.因x1∈V1，u∈V2，得

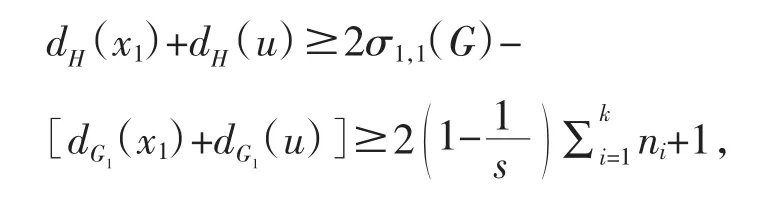
从而在H中存在一个圈Ci，使得

因为ni≥s，故有dci（x1）+dci（u）≥2s－1＞s+1.由引理2及Ci的最小性可知l（Ci）=2s,根据引理3，可知存在点x0∈V（Ci）∩V2，使得C′i=Ci－x0+u包含一个长至少为 2s的圈，且 x0x1∈E（G）.用 C′i替换 Ci，我们得到Ci中的一条路P′=x0x1…xp.这与最长路P的选择矛盾.从而p=2d，故G中存在一条Hamilton路.

定理1 设s≥3，G（V1，V2）是一个均衡二部图,满足+1.如果G包含k个顶点不交的长至少为2s的圈,则有一个至少包含k个顶点不交的长至少为2s的圈的 2－因子.

证明:设t是最大的整数,使得G有t个长至少为2s的顶点不交的圈,满足包含一条Hamilton路.也就是说我们选择的长至少为2s的顶点不交的 t个圈，C1，C2，…，Ct，使得最大,由引理5知,t≥k.设l（Ci）=2ni，对所有的i∈｛1,2,…,t｝.显然 ni≥s，令

设p=x1x2…x2d是G1中的一条Hamilton路,由的最大性及引理4知dGi（x1）+dGi（x2d）≤ni,对所有的 i∈｛1，2,…，t｝,故有

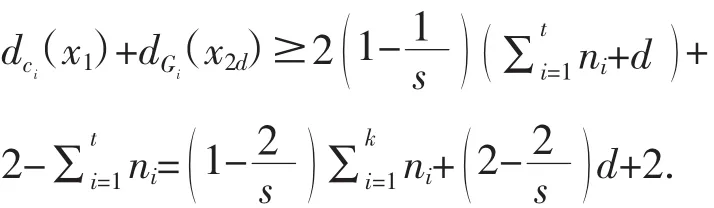
因为 ni≥s，且 t≥k≥2,d≥1,则有

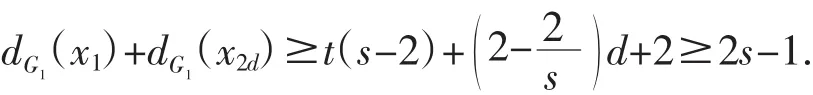
从而有dG1（x1）≥s,或dG1（x2d）≥s.显然在G1中存在一个长至少为2s的圈,这与t的最大性矛盾,故有即定理得证.

[1]Dirac G.Some theorems on abstract graphs[J].Proc London Math Soc,1952,2:69-81.

[2]Yan Jin,Liu Guizhen.On 2-factors with large cycles in a balanced bipartitegraph[J].Chinese Journal of Engineering Mathematics,2004,21(6):910-914.

[3]Bondy J A,Murty U S R.Graph Theory with Applications[M].New York:American Elsevier,1976.

[4]Wang H.Larg Vertex-disjoint cycles in bipartite graph[J].Graph Comb,2000,16:359-366.

[5]Wang H.On 2-factors of a bipartite Graph[J].Graph Theory,1999,31:101-106.