Q(Qr)空间及其性质

黄利忠，罗 成

(1.山西大同大学数学与计算机科学学院，山西大同 037009;2.内蒙古大学数学科学学院，内蒙古呼和浩特 010021)

20世纪早期，Banach给出了完备的赋范线性空间上的开映射定理和闭图象定理[1].随后，Robertso兄弟和V.Ptak等一批工作者对某些局部凸分离空间做了系统且深入的探讨，给出了相应的闭图象定理[2，3].在文献[2]中关波对G(Gr)空间做了一定的研究.受此启发，本文中，我们将qw*闭概念中的“θ点邻域”用“包囿桶”来代替，提出了qw*闭的概念，进而提出了Q空间与Qr空间的概念，并对这两个空间的性质做了简单的探讨.在本文中，若不加以说明，（X，T）均指局部凸Hausdorff空间(简记为lcs空间).若无特别声明，文中所用的符号均与文献[2]保持一致.

1 预备工作

定义1[2]设（X，T）是lcs空间，共轭空间X′中的子集N称为是aw*闭的，如果对于X中的每个θ点邻域，B0∩N是X′中的弱*紧集.

定义2[2]称lcs空间（X，T）是B完备(或称全完备，空间是Ptak空间)，如果在X′上的每个aw*闭的线性子空间是弱*闭的;称lcs空间（X，T）是Br空间(或称inf ra-Ptak完备)，如果X′中每个弱*稠密的qw*闭的线性子空间是弱*闭的.

下面我们给出qw*闭的概念.

定义3 设（X，T）是lcs空间，共轭空间X′中的子集N称为是qw*闭的，如果对于X中的每个包囿桶B，B0∩N是X′中的弱*紧集.特别地，X′是qw*闭的当且仅当对X中的每个包囿桶B，B0是X′中的弱*紧集.

从定义分析，我们不难得出下面几条简单的性质.

(1)若将定义中的包囿桶B换成θ点邻域，则上述定义中qw*闭就是我们熟知的aw*闭的概念.显然，qw*闭集是aw*闭的;

(2)由于包囿桶是桶，所以gw*闭集是qw*闭集也是Aw*闭集;

(3)qw*闭，gw*闭与Aw*闭都具有相容不变性.特别地，当（X，T）是桶空间时，X′中子集合的这三种闭性质和aw*是相互等价的;

(4)qw*闭集的弱*闭子集是qw*闭的.

引理1 设（X，T）是Mackey空间，则下列陈述是等价的:

(1)X是拟桶空间;

(2)X′是 qw*闭的;

(3)X′的每个弱*闭的线性子空间是qw*闭的;

(4)X′的每个弱*闭子集是qw*闭的;

(5)X′中的qw*闭集与aw*闭集是一致的.

证明(5)⇒ (4)设X′上的qw*闭集与aw*闭集是一致的，N是X′的弱*闭集，由于弱*闭集一定是aw*闭的，所以N是aw*闭的，从而由条件知是qw*闭的.

(4)⇒(3)这是显然的.

(3)⇒ (2)设X′的每个弱*闭的线性子空间是qw*闭的.X′作为特殊的弱*闭子空间当然是qw*闭.

(2)⇒ (1)设X′是qw*闭的，B是X中的任意包囿桶，由条件可得B=B∩X′是绝对凸的弱*紧集.因为X是Mackey空间，由Mackey-Arens定理，B00∈N(X)，又因为B是桶，由双极定理可知，B=B00，于是B∈N(X).所以X是拟桶空间.

(1)⇒(5)设X是拟桶空间，即X中每个包囿桶都是X中的θ点邻域，所以X′上的qw*闭集与aw*闭集是一致的.

下面我们在前面给出的qw*闭集的基础上，给出Q空间及Qr空间的概念.

定义4 称lcs空间（X，T）是Q空间，如果X′中每个qw*闭的线性子空间是弱*闭的;称lcs空间（X，T）是Qr空间，如果X′中每个弱*稠密的qw*闭的线性子空间是弱*闭的.

从定义上看，Q完备空间一定是Qr完备空间.由于集合的qw*闭性质具有相容不变性，所以空间的Q(Qr)性质都具有相容不变性.

2 主要结果

定理1设（X，T）（Y，S）都是lcs空间，u:（X，T）→（Y，S）是连续线性算子且将X中的包囿桶映为Y中的包囿集，则u′保持qw*闭集.

证明 N是Y′中的qw*闭集，B是X中的任意包囿桶，令 A=B0∩u′(N).下证 A=u′⌊(uB)0∩N」.

设 f∈A，则 f∈B0且 f∈u′(N).由 f∈u′(N)存在g∈N，使得 f∈u′(g).对任意的 y∈u(B)，存在 x∈B，使得 y∈u(x).由于 f∈B0，有

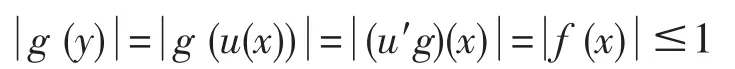
所以

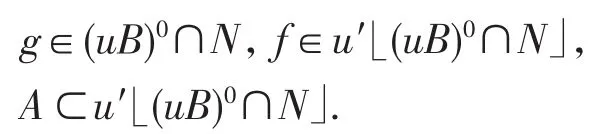
反之，任取g∈(uB)0∩N，x∈B，令 f∈u′(g)，则有

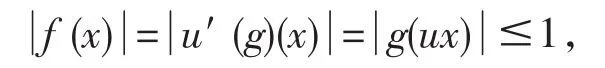
所以，f∈B0，f∈B0∩u′(N),

u′⌊(uB)0∩N」⊂A.综上，

A=u′⌊(uB)0∩N」.

由于u将X中的包囿桶映为Y中的包囿集，所以u(B)是Y中的绝对凸包囿集，从而是Y中的包囿桶.而N是Y中的闭集，所以是Y′中的弱*紧集，又所以((uB)

)0∩N是Y′中的弱*紧集.u是连续的，由引理 u′是弱 * 连续的，于是 A=u′⌊(uB)0∩N」是 X′中的弱*紧集，所以u′(N)是qw*闭的.

推论设（X，T）（Y，S）都是lcs空间，u:（X，T）→（Y，S）是连续线性算子且将X中的包囿桶映为中的包囿集.若Y是Q空间，则Y也是Q空间

证明 N是Y′上的qw*闭的线性子空间，算子u′是u的共轭算子.由于u是T-S连续的线性算子且将X中的包囿桶映为Y中的包囿集，由引理1， u′保持 qw*闭集，所以 u′(N)是 X′中的 qw*闭的线性子空间.而X是Q空间，所以u′(N)是弱*闭的.由于 u是在上的，u′是单射，有而u′是弱*连续的，所以N是弱*闭的.因此Y也是Q空间.

[1]Taylor A E.Introduction to Fuctional Analysis(second edition)[M].New York:John Wiley&sons，1980.

[2]关波.G空间与开映射定理，数学杂志[J].1986，6(2):157-164.

[3]Kalton N J.Some Forms of The Closed Graph Theorem[J].Proc Cambrige Philos Soc，1971，70:401-408.

[4]Wilansky A.Modern Methods in Topological Vector Spaces[M].New York：McG-raw-Hill，1978.