双互易杂交边界点方法求解Helmholtz方程＊

杨庆年，郑俊杰，苗 雨

（1.华中科技大学土木工程与力学学院，湖北武汉 430074；2.南阳理工学院土木工程系，河南南阳 473004）

亥姆霍兹（Helmholtz）方程▽2u＋μ2u＝f是一个椭圆形偏微分方程［1－2］，在高波数的情况下它的解呈现高振荡的特性，因此它的求解对数值方法是一个挑战.传统数值方法的求解精度有待提高，如有限元法的计算精度随着方程波数的增大而急剧降低，这是因为有限元法普遍采用了低阶的多项式作为位势函数的插值函数，而低阶多项式不可能对高频震荡的波传播问题给出很好的近似，要提高计算精度，必须大幅度增加单元网格的数量，计算工作量大，效率低，不适应实际复杂大规模问题的求解.解决这个问题，单靠计算机硬件的发展是远远不够的，必须寻找适应性较强的高效计算方法，以提高解决实际问题的能力.

杂交边界点方法［3－6］是一种纯边界类型的无网格方法，该方法无论插值还是积分都不需要网格，计算时仅需要边界上离散点的信息，前处理简单，是一种很有发展前景的计算方法.然而，该算法同其他边界类型方法一样，在求解Helmholtz方程这样的非齐次方程时需要域内划分网格，从而失去了其降维的优势.本文将杂交边界点方法同双互易法［7－8］结合，提出了一种求解Helmholtz方程的新方法，该方法将问题的解分为通解和特解两部分，通解使用杂交边界点法求解，特解则使用径向基函数插值得到，数值算例表明该方法计算精度高，稳定性好，计算时需要域内布置节点，但仅用来径向基函数插值，因此不影响该方法降维的优势.

1 Helmholtz方程求解的杂交边界点法

为方便起见，可假定f＝0，Helmholtz方程可表示为

式（1）的左端项利用杂交边界点法求解拉普拉斯方程，右端项使用径向基函数插值.根据双互易定理，式（1）的解u可分为通解uh和特解up两部分，即

特解up仅仅需要满足非齐次方程

通解uh必须满足拉普拉斯方程和修正边界条件：

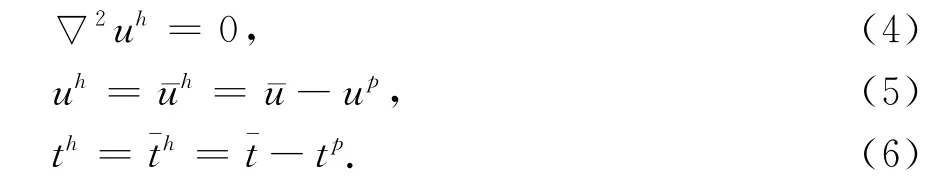
通解利用杂交边界点法求解.杂交边界点法基于修正变分原理，在修正变分原理中，假定域内位移场u，边界位移场和边界面力是相互独立的，域Ω的边界为Γ＝Γu＋Γt，和分别是Γu和Γt上的边界值，相应的修正变分泛函ΠAB定义为

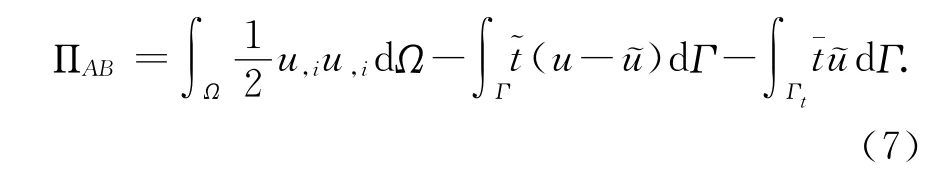
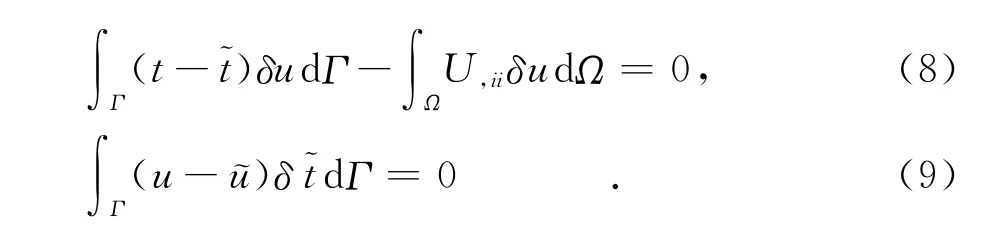
由δΠAB＝0，可得下面弱积分方程：式（8）和式（9）在域Ω的任何一部分都成立.例如，对于图1所示的以sJ为圆心的子域Ωs［9］，边界为Γs和Ls.对于子域Ωs，我们采用下面的弱积分形式代替式（8）和式（9）.

式中：h为检验函数.

图1 子域Ωs以及相应基本解的源点SJFig.1 Local domainΩsand source point of fundamental solution corresponding to SJ

为了使Ls上积分为零，检验函数h取类似于移动最小二乘权函数的形式：

式中：dJ是域内任意点Q到节点sJ的距离.和用移动最小二乘近似［10］插值：

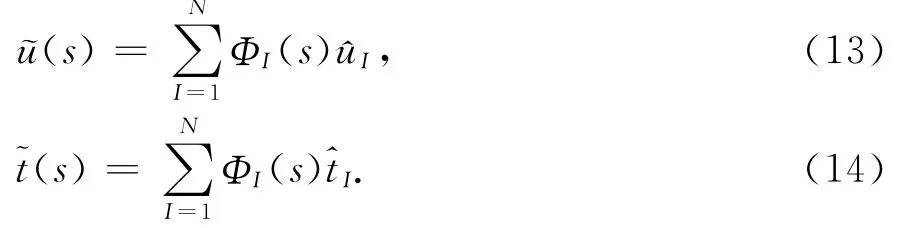
域内变量使用基本解近似：

基本解的形式为

式中：r是场点Q到源点PI之间的距离.

当u采用式（15）时，式（10）和（11）可写成：

对所有节点列出上面方程，则有

式中：

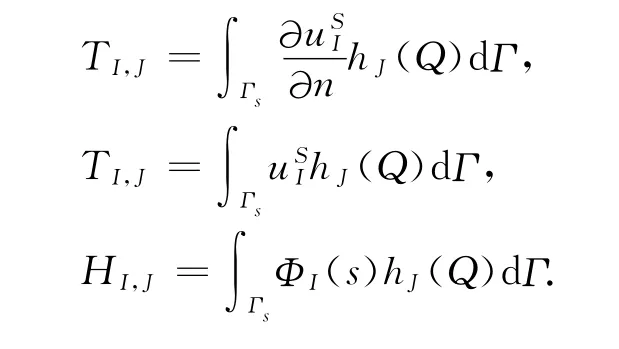
2 双互易杂交边界点法

2.1 双互易法

利用双互易法求解Helmholtz问题是将非齐次应用出现的域内积分转化为等价的边界积分，对非齐次项进行插值，－μ2u用式（22）近似.

式中：αj是一系列初始未知参数；fj是近似函数；N和J分别是边界点总数和域内点总数.

作为方程的相同形式，特解根据特解的基本形式进行插值：

如果up满足方程（3），可得如下方程

选取fj＝1＋r＋r2，显而易见，满足式（24）的特解=u为

相应的面力为

通过式（22），（23）和（24），特解写成矩阵形式：

2.2 双互易杂交边界点方法

杂交边界点方法采用移动最小二乘插值形成形函数，不满足δ特性，故边界条件需作处理.本文采用实值虚值交换法处理修正的边界条件［11］，有：

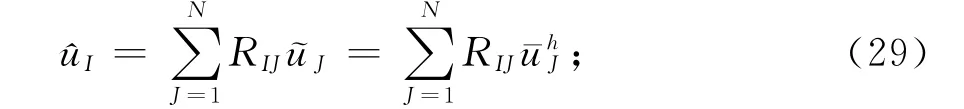
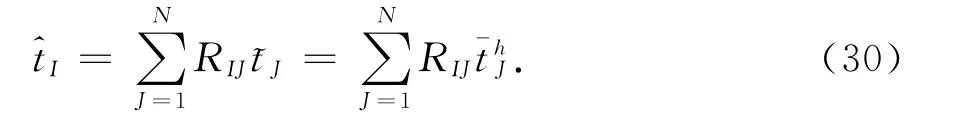
式中：RI，J＝［Φ，J（SI）］－1，N是该边界节点总数；和是节点通解.

将式（27）～（30）代入式（2），然后将结果代入式（20）和（21），得

式（31）和（32）是双互易杂交边界点法求解亥姆霍兹问题的系统方程，假设N个点位于边界上，通过式（31）和（32）可得到N个方程.但是，上面的方程包含L个内部点的位移，所以附加方程是必须的.

2.3 附加方程

利用式（31）和（32）不能求出域内点的变量，因此，本节研究求解Helmholtz问题的附加方程.

域内点未知变量用下式表达：

通解uc用基本解插值，特解up用式（27）表示，因此式（33）可表示为

式中：u＊是域内点的位移；uS是域内点基本解矩阵；是特解基本形式的值的矩阵.

由式（32）求得

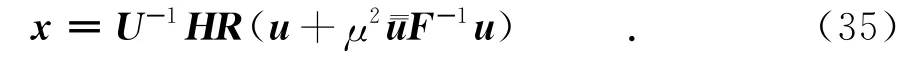
将式（35）代入式（34）得

将式（35）代入式（31）得

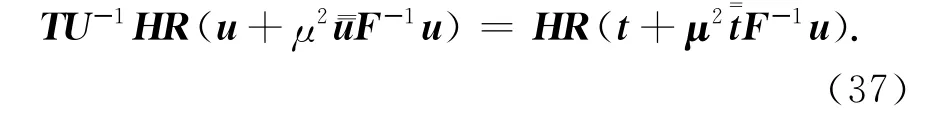
联立方程（36）和（37）得

其中

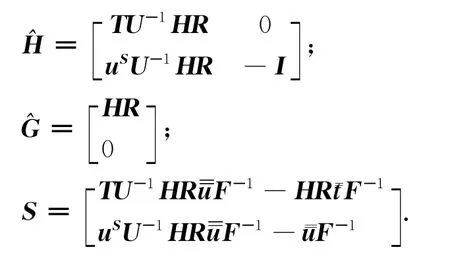
以上就是双互易杂交边界点法求解Helmholtz问题的理论推导过程.像边界元法，本文提出的方法也存在“边界层效应”，本文使用一种自适应积分方案来解决这一问题.双互易杂交边界点方法是一种仅在边界上布点的无网格方法，无论插值还是积分都不需要边界单元，域内的点仅仅是为了特解插值的需要，不影响该方法是一种边界类型的方法.

3 数值算例

本文以两种不同边界条件的振动梁作为研究对象，为了验证该算法的计算精度，相对误差定义为：

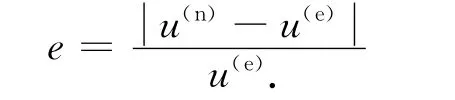
式中：（e）和（n）分别表示解析解和数值解；u表示位移.

3.1 悬臂梁的振动

如图2所示的悬臂梁，梁长0.9m，用40个边界点和24个域内点离散，在固定端中部的边界点（点40）处施加一个任意小的位移u0，其余所有点t＝0.

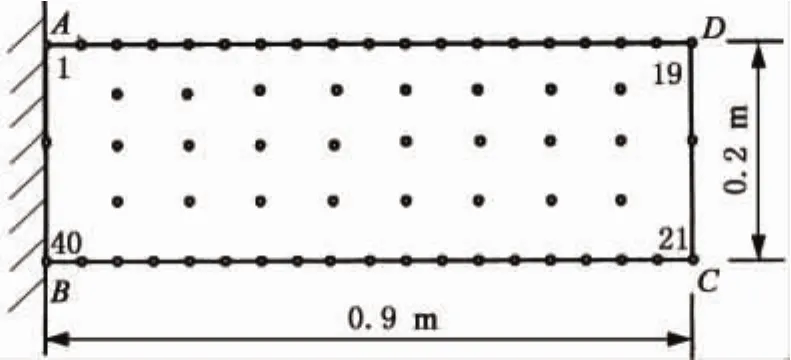
图2 悬臂梁的计算模型Fig.2 Discretization of the cantilever

固有频率的解析解为［8］

对于一维问题，变形模态为

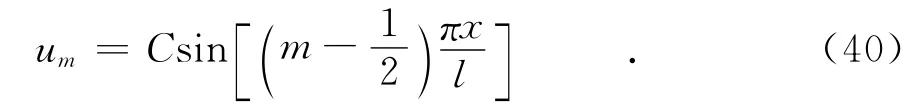
式中：m是初始期望阶次的整数值；l是梁的长度；C是任意常数.

根据式（39），梁的固有频率的表达式为

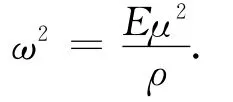
式中：ρ和E是材料常数；当C被定义时，式（40）求出变形模态，本文取C＝1.

当利用式（38）计算时，取μ＝0，▽μ＝0.1.如果连续两次迭代所有点的u值平均增长30%，Δμ可减为0.01；当u的平均值开始下降时，Δμ提高到0.5，直到u值再增加时为止.

计算时，把振动梁的边界分为4片光滑的边界段.在边界上均匀布置40个点（在AD和BC上各布置19个点，在AB和CD上各布置1个点），即N＝40，在域内布置24个点，即L＝24.图3为第1～4级固有频率时梁的变形图.从图中可以看出，数值解和解析解吻合得非常好.

图3 1～4级固有频率悬臂梁的变形图Fig.3 Deformed shape for first four natural frequencies of cantilever

为了分析计算精度对边界点数量的敏感性，我们分为6种不同情况，每种情况的相对误差如图4所示.从图中可以看出，域内点的数量对这类问题的影响还是比较明显的，特别是高阶振动模态.

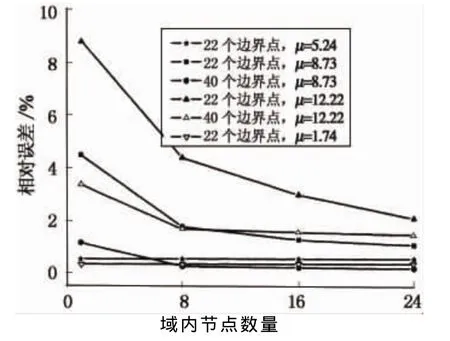
图4 1～4级固有频率悬臂梁的变形图Fig.4 Deformed shape for first four natural frequencies of cantilever

3.2 两端固支梁的振动

如图5所示的两端固定梁，梁长0.9m，点的布置与图2相同，在左端中部的边界点（点40）处施加一个任意小的位移u0，其余所有点t＝0.

固有频率的解析解为［8］

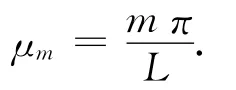
对于一维问题，变形模态为

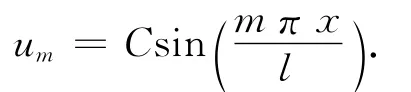
表1为在不同离散方案情况下μ数值解与解析解的比较.

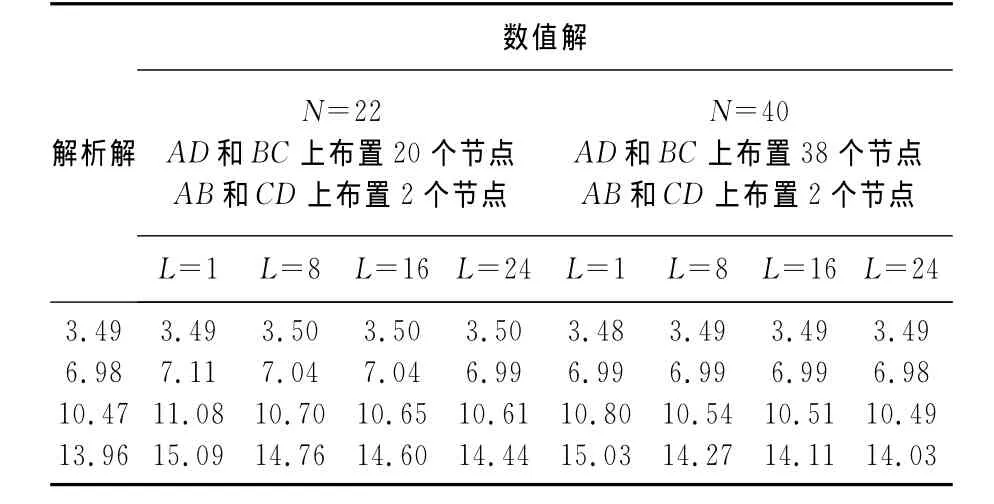
表1 μ数值解与解析解的比较Tab.1 Comparison of numerical and analytical solution forμ

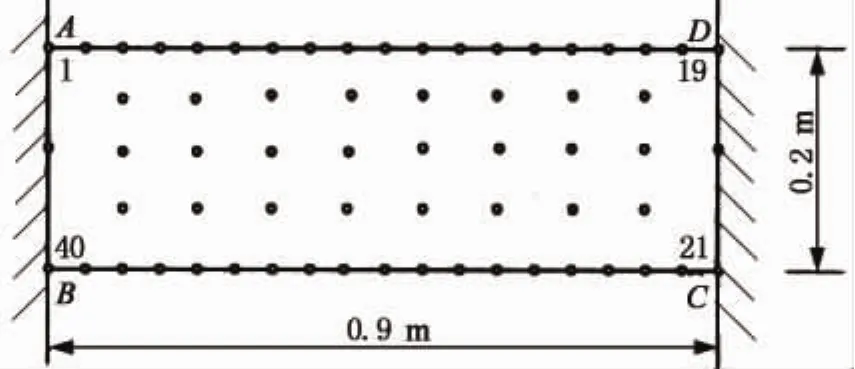
图5 两端固定梁计算模型Fig.5 Discretization of the clamped－clamped beam

4 结 论

本文将双互易法和杂交边界点法结合求解Helmholtz方程，该算法无论插值还是积分都不需要网格，是一种边界类型的纯无网格法，域内布置少量节点仅仅用来径向基函数插值.数值算例表明，该方法在求解Helmholtz方程时计算精度高，前处理简单，适合求解此类问题.

通过数值算例可以得出以下结论：

1）域内点的位置和数量在低阶振动模态分析中，对计算结果的影响并不大，但在高阶振动模态的分析中是很重要的，由数值算例看，域内节点数量只要保证不低于边界节点数量的一半就可以满足计算精度要求.

2）子域半径的大小对计算结果影响较大，一般取0.8h～0.9h较为合适，h为相邻节点之间在参数空间的平均距离.

3）利用该算法求解振动梁的变形模态具有高精度和高收敛性，在杂交边界点法求解中的边界层效应通过自适应积分方案来解决.该方法还可用于求解更为复杂的非齐次问题.

［1］ CHEN J T，WONG F C.Dual formulation of multiple reciprocity method for the acoustic mode of a cavity with a thin partition［J］.Journal of Sound and Vibration，1998，217：75－95.

［2］ HARARI I，BARBONE P E，SLAVUTIN M，et al.Boundary infinite elements for the Helmholtz equation in exterior domains［J］.International Journal of Numerical Method in Engineering，1998，41：1105－1131.

［3］ ZHANG J M，YAO Z H，MASATAKA T.The meshless regular hybrid boundary node method for 2Dlinear elasticity［J］.Engineering Analysis with Boundary Elements，2003，27：259－268.

［4］ MIAO Y，WANG Y H.Development of hybrid boundary node method in two dimensional elasticity［J］.Engineering Analysis with Boundary Elements，2005，29：703－712.

［5］ ZHANG J M，YAO Z H，LI H.A hybrid boundary node method［J］.International Journal of Numerical Method in Engineering，2002，53：751－763.

［6］ ZHANG J M，TANAKA M，MATSUMOTO T.Meshless analysis of potential problems in three dimensions with the hybrid boundary node method［J］.International Journal of Numerical Method in Engineering，2004，59：1147－1168.

［7］ WROBEL L C，BREBBIA C A.The dual reciprocity boundary element formulation for non－linear diffusion problems［J］.Computer Methods in Applied Mechanics and Engineering，1987，65（2）：147－164.

［8］ PARTRIDGE P W，BREBBIA C A，WROBEL L C.The dual reciprocity boundary element method［M］.Southampton：Computational Mechanics Publications，1992.

［9］ ZHU T，ZHANG J D，ATLURI S N.A local boundary integral equation（LBIE）method in computational mechanics，and a meshless discretization approach［J］.Computational Mechanics，1998，21（3）：223－235.

［10］LANCASTER P，SALKAUSKAS K.Surfaces generated by moving least squares methods［J］.Mathematics of Computation，1981，37：141－158.

［11］ZHU T，ATLURI S N.A new meshless local Petrov－Galerkin（MLPG）approach in computational mechanics［J］.Computational Mechanics，1998，22（2）：117－127.