基于网格聚类中边界点的处理
江先伟(福建船政交通职业学院 福建 福州 350007)
0 引言
基于网格的聚类方法是运用网格技术,把对象空间量化为有限数目的网格单元,形成一个网格结构,所有的聚类操作都在这个网格结构上进行。一个网格单元的邻居是指与其有共同边界的或有共同点的那些网格单元。一个网格单元包含对象的数目超过给定的密度阈值MinPts,则认为它是高密度单元,否则视其为低密度单元。连接相邻密集单元的最大区域就形成一个“簇”,在这个区域内的所有对象属于这个簇。对孤立点,在聚类过程中应该将其丢弃,如果一个低密度单元的相邻的网格单元中存在高密度单元,那么该单元中的点可能是簇的边界点,也可能是噪声点,为此,可利用边界处理技术作进一步处理。
聚类的边界代表了一种潜在的模式,对数据挖掘有着重要的意义。但是目前涉及边界的算法并不多,对其研究远远不够。另一方面,边界点处于某些簇的相邻位置,许多聚类算法(如基于网格的方法)不能准确地把这些边界点划分到对应的簇中,从而降低了聚类结果的质量。
1 相关工作
1.1 边界点的定义
在DBSCAN算法中,第一次提出了边界点的概念。算法是基于密度定义了簇的边界点,即如果一个对象不是核心点(所谓核心点指的是某对象的ε-邻域内至少包含最小数目MinPts个对象),且它是从某个核心点直接密度可达的 (即该对象落入某核心点的ε-邻域内),则定义该对象为边界点。
Chen Xia等提出了聚类边界点检测算法BORDER[1],其边界点的定义如下:
定义 边界点(Boundary point):一个边界点p是指满足下列两个条件的数据对象:
①它位于一个高密的区域IR;②p的附近存在一个区域IR′,Density(IR)>>Density(IR′),或者 Density(IR′)>>Density(IR)。
聚类的边界代表了一种潜在的模式,对数据挖掘有着重要的意义。但是目前涉及边界的算法并不多,对其的研究远远不够。另一方面,边界点处于某些簇的相邻位置,许多聚类算法(如基于网格的方法)不能准确地把这些边界点划分到对应的簇中,从而降低了聚类结果的质量。
1.2 边界点的处理方法
DBSCAN算法基于密度定义了聚类边界点,即如果一个对象不是核心点,且它是从某个核心点直接密度可达的,则定义该对象为边界点。提出聚类边界提取的BORDER算法中,应用反向k近邻可以反映出潜在的数据分布特征,并可以利用它识别位于两个或多个分布之间的边界点。BORDER算法认为边界点的反向k近邻个数低于聚类内部点的反向k近邻个数,如果一数据点的k近邻个数低于某阈值则把其作为边界点输出。该算法的缺点是:①在含有噪声的数据集中,因为噪声点的反向k近邻个数往往比聚类边界点的反向k近邻个数少,因此按照对象的反向k近邻值从小到大顺序排列整个数据集后,取出的前n个对象既包含孤立点又包含边界点,因此该算法在含有噪声的数据集上不能正确地识别边界;②BORDER算法不能正确地提取变化密度、多密度聚类中的边界,因为低密度点的反向k近邻值较小,而高密度点的反向k近邻值较大。
文献[2]提出了利用正负半邻域关系来判断聚类的点检测算法,首先提出正负半邻域的概念,进而计算出数据点的边界度,根据边界度进行边界点的提取。它解决了DORDER算法不能将边界与噪声分离的问题。
1.3 在网格中边界点的处理
传统基于网格的聚类算法只处理高密度单元,低密度单元中的点作为孤立单元被丢弃,一旦聚类的边界落入低密度单元,就会降低聚类精度,可能造成小聚类的丢失。并且,算法只能发现边界是水平或垂直的簇,而不能检测到斜的边界,在大多数情况下这是不符合实际的。如何有效地提取边界点,是提高聚类结果的质量的关键问题之一。
边界单元和核心单元形成聚类簇的主要轮廓,而边界点充实该轮廓,有时聚类簇的边界点可能落入聚类结果网格单元以外的网格单元中,这就需要将聚类的边界点从这些单元中提取出来,划分到对应的簇中,以提高聚类的精度。边界点提取有两种方法:一种方法,是对与边界单元相邻而未聚类的网格单元进一步细分,如在每一维上再二等分,则每个边界单元被划分为2d个子单元,如果在这些子单元中存在与边界单元相连接的子单元,则子单元中的对象视为边界点,提取到相应的簇中;另一种方法,是基于这样一个事实:簇中对象的密度高于簇外部的密度和边界点的密度,聚类边界的密度到聚类外部的密度有明显的跳变,每次聚类都从未聚类中最高密度的网格单元开始逐步向外扩展,遇到边界单元时进行边界处理。对于一个与边界网格单元g1相连的非密集单元g2,在非密集单元g2中取一个与边界单元g1最近的点x,使用KNN近邻关系法,在x和单元g1内的点中观测x的密集程度,来判断x是否作为边界点提取。如果是则用同样的方法对下一对象进行处理,否则,x不能作为边界点被提取。
文献[3]出了基于网格的聚类的边界处理技术,该技术利用限制性k近邻和相对密度的概念识别网格聚类的边界点,提高聚类的精度。
2 本文提出的边界处理技术
受DBSCAN算法的启发,本文提出的边界处理方法是在网格结构中引入边界网格单元和孤立网格单元的概念,依据边界网格单元中包含对象的数目,定义该边界单元的核心点,并依据核心点的ε-邻域内所有对象都属于同一个簇的原则提取与边界单元相邻的孤立网格单元中的对象。
本文定义的边界网格单元:属于某一簇的网格单元g,在它相邻的网格单元中,存在与单元g属于不同簇的单元或存在未聚类的单元,则将单元g定义为边界网格单元,并称单元g是其所属簇的边界网格单元。从与边界网格单元相邻的孤立网格单元中提取靠近的点对象,这种“靠近”的准则是:待提取点对象位于边界网格单元中某一核心点的Step/2-邻域内,则把该点对象作为边界点提取到对应的边界网格单元中。
以边界网格中的某点对象为圆心,Step/2为半径的圆内包含点对象的数目达到值τ:则该点对象定义为该边界单元的核心点。

其中,n0为该边界网格单元的密度值。值τ实际上就是该边界网格单元密度平均值的1/DCT倍取整。
如图所示,带阴影的网格单元(标号为1~6)属于同一个簇,标号为7~9的网格单元为孤立网格单元,其中点对象c是边界网格单元(标号为5)的核心点,而孤立网格单元(标号为8)中的点对象o落在核心点c的Step/2-邻域内。则把点对象o作为边界点提取到边界网格单元5中。
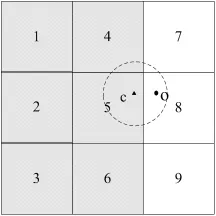
边界点的处理
对孤立网格单元中点对象的提取只须判断其Step/2-邻域内是否存在边界单元的核心点,如果存在,则把点对象o提取到该核心点所在的边界网格单元中。当提取点对象o后,如果点o的Step/2邻域内包含的点数超过值τ,则点o也成为边界网格单元的核心点,这样边界点的提取可以逐步向外延伸。
3 结束语
基于网络聚类算法中,效率与精度总是一对矛盾。对孤立点,在聚类过程中应该将其丢弃,如果一个低密度单元的相邻的网格单元中存在高密度单元,那么该单元中的点可能是簇的边界点,也可能是噪声点,为此,可利用边界处理技术作进一点的处理。本文提出一种应用密度的思想对边界点进行处理技术,可一定程度上提高基于网格聚类的精度。
[1]ChenXia,wynne Hsu,Mong Li Lee et al.BORDER:Efficient computation of boundary points[J].IEEE transaction on knowledge and data engineering.2006,18(3):289-303.
[2]Qiu,B Z,Yue F,Shen J Y et al.A efficient boundary points detecting algorithm.Proceedings of Advances in Knowledge Discovery and Data Mining(PAKDD)[M].New York:ACM Press.2007,4426:761-768.
[3]邱保志,刘洋.基于网格熵的边界点检测算法[J].成都:计算机应用.2008,28(3):732-734.

