基于改进遗传算法辨识空间机器人动力学参数

刘 宇，李瑰贤，夏 丹，徐文福

(1.哈尔滨工业大学基础与交叉科学研究院，哈尔滨150001，lyu11@hit.edu.cn;2.哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨150001;3.哈尔滨工业大学机电工程学院，哈尔滨150001)

空间机器人名义动力学参数通常偏离其实际的动力学参数，而其运动规划所用的广义雅克比矩阵包含动力学参数，这意味着动力学参数的误差将导致其末端位姿轨迹的误差，从而影响了空间机器人在轨执行任务的能力.因此，有必要寻求一种经济可行的方法实现对空间机器人动力学参数的在轨辨识.与地面机器人相比，空间机器人的基座是漂浮的，相当于增加了6个自由度.由于空间微重力环境的影响，针对地面机器人的重力平衡辨识方法无法使用，而目前用于空间机器人基座与关节的加速度和驱动力/力矩传感器信噪比较低，这些因素均使空间机器人的动力学参数辨识遇到困难.V.A.Sujan和S.Dubowsky［1］提出了基于交互信息的可观测性指标，用于产生最优外部激励.该方法假定系统装配有加速度计、倾角计以及六维力/力矩传感器，通过测量机械臂运动对基座作用的力/力矩，采用Kalman滤波器进行在线的动力学参数辨识.R.Lampariello和 G. Hirzinger［2］则对动力学方程重新组织(经运动分解去除轨道部分的影响后，得到新的状态空间，其矢量为在轨道坐标系下的表示)，将相对于惯性系的矢量(特别是平移运动矢量)在局部坐标系中进行表示，以解决实际中不能直接得到相对于惯性系测量的问题，但辨识中需要基座的加速度、关节力矩以及关节加速度的测量数据.Y.Gu和Y.Xu［3］讨论了基座姿态受控情况下的动力学参数辨识问题，将动力学方程在关节空间进行了参数线性化表示.Y.Xu［4］等提出了“扩展机器人”(extended robot)的概念，将空间机器人系统的动力学方程在笛卡尔空间进行参数线性化表示.Y. Murotsu［5］等研究了空间机器人捕获未知目标后载荷动力学参数的辨识问题，提出了两种辨识方法，分别用到了基座线速度、线加速度测量以及关节力/力矩传感器的测量.R.Katoh等［6］也研究了目标捕获载荷后的参数辨识及控制问题.Satoko Abiko和Kazuya Yoshida［7］研究了柔性空间机械臂捕获目标后的动力学参数辨识问题，同时，借助重力梯度力矩还辨识了ETS-VII上各杆件的质量、惯量以及质心位置［8］.该方法用到了ETSVII的飞行数据，但其不能辨识各杆质心位置，而是假定其已知，这使得辨识精度不甚理想.R. Lampariello［9］等根据德国GETEX(德国在ETSVII)所做的动力学实验的经验，提出了基于加速度计的参数辨识方法，并针对3个辨识问题(基座惯性参数的辨识、载荷惯性参数的辨识以及整个空间机器人系统惯性参数的辨识)，研究了相应的动力学建模和实验设计.国内在这方面的研究较少，哈工大何光彩等［10］采用神经网络的方法，辨识基座和捕获载荷的质量，但对于动力学参数的辨识，没有太多的研究.

本文利用基于改进的遗传算法对空间六关节机器人的动力学参数进行辨识，并给出仿真结果.

1 角动量守恒方程

1.1 基本假设与变量定义

空间机器人系统由卫星本体和机械臂组成，如图1所示.建立系统运动学模型时，需作如下假设:

1)连接机械臂各构件的关节均为转动关节，具有一个旋转自由度，没有其他机械约束作用.

2)忽略重力梯度力矩及其他环境力矩影响，系统相对轨道坐标系的运动可以认为无外力和外力矩作用，系统的线动量和角动量守恒.

图1 空间机器人的一般模型

图1是具有单一机械臂的自由漂浮空间机器人的一般模型，它由n个关节的机械臂和作为基座的卫星本体组成.刚体0代表卫星本体，刚体i代表机械臂的第i个连杆，从本体往上编号依次为1～n.Ci表示第i个连杆的质心;连杆i-1和连杆i通过关节i连接.采用D-H规则建立各连杆的坐标系，用Σi表示第i个连杆坐标系，Oi表示其原点(其中O0为卫星本体的质心);Og为整个系统的质心;ΣI为惯性系.

为方便讨论，各符号定义如下(注:ix为矢量x在坐标系Σi中的表示，如不特别注明，均为在惯性坐标系中的表示):

Θ =［θ1，θ2，…，θn］T∈Rn为机械臂关节角向量;ri∈R3为连杆i的质心位置矢量，rg∈R3为整个系统质心的位置矢量;pi∈R3为坐标系Σi原点的位置矢量;ai∈R3为矢量;bi∈R3为矢量;li为矢量;v0∈R3为卫星本体质心处的绝对线速度(=˙r0);ω0∈R3为卫星本体的绝对角速度;vi∈R3为连杆i质心处的绝对线速度(=˙ri);ωi∈R3为连杆i的绝对角速度; mi为连杆i的质量;M为整个系统的总质量，Ii∈R3×3为连杆i的惯性张量.

再定义如下的操作数:如果r=［x，y，z］T，则

1.2 各矢量位置关系

如图1所示，坐标系Σi原点的位置矢量如下:

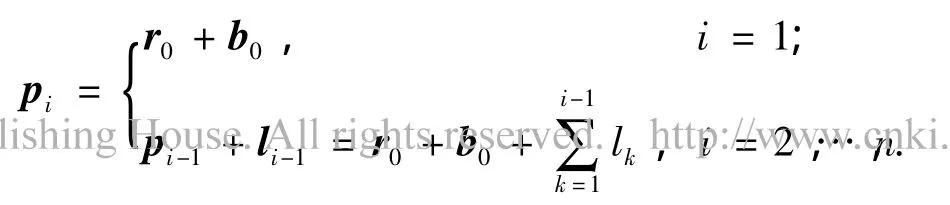
各连杆质心的位置矢量

将惯性参考系选在系统质心rg=［0，0，0］T，由，可以求出r0:

各杆件质心处的速度在惯性系中的表示:

另一方面，各刚体质心及末端的角速度可表示为

1.3 角动量守恒

假设整个系统不受外力和外力矩，则系统的角动量守恒.设L表示系统角动量(相对于惯性坐标系)，则

将式(1)和式(2)代入式(3)，可得

式中:

如前所述，惯性参考系选在系统质心，式(4)可简化为

一般情况下，空间机器人系统安装了用于基座姿态控制的反作用力飞轮，因此，还需要在式(3)中加入飞轮的角动量LRW.这样，式(5)可以重新修正如下:

2 基于改进遗传算法辨识动力学参数

2.1 待辨识参数

一般地，空间机器人动力学在轨参数包括基座质量、质心位置、惯性矩、惯性积以及机械臂各个连杆质量、质心位置、惯性矩、惯性积.需辨识的动力学在轨参数数目为k=10(n+1)，n为机器人的关节数，用矢量q表示

式中:

根据式(7)，对于一个六关节空间机器人，其待辨识动力学参数达70个.在本文中，为了简化辨识模型，仅取动力学参数中影响较大的质量和惯性矩进行辨识，这样，辨识参数减少到28个，即:

式中:

2.2 动力学参数辨识的偏差模型

Iw和Iφ包括了未知的待辨识的动力学在轨参数q.由方程(6)，LRW可以表达为q的函数，即

假设LRW是实际测量而来的，~LRW是基于当前卫星本体的角速度ω0、关节角速度 ˙Θ和名义动力学在轨参数q估计而来.名义动力学参数与真实动力学参数之间的误差Δq导致反作用飞轮的测量值与估计值存在误差ΔLRW，可表示如下:

ΔLRW=LRW-~LRW=f(q+Δq)-f(q).

2.3 改进的遗传算法

将传统的遗传算法应用于六关节的参数辨识，发现辨识结果容易出现“早熟现象”，不能保证辨识结果收敛到最优.但由于遗传算法处理的群体是有限的，因而存在随机过程，使群体中个体的多样性过早地丢失，从而使算法陷入局部最优点.

本文从初始群体的生成、精英个体的保留以及大变异操作等方面对传统的遗传算法进行了改进，能有效地克服早熟现象，明显提高收敛速度，并具有优良的自适应特性.

1)小区间生成

即依据待辨识参数的取值范围，将其约束为确定的小区间，再在各小区间内随机生成各个参数，组成种群内的个体.这样可根据已知的实际情况，保证所选择的个体在可行域内，减小了不必要的搜索，提高了搜索效率.

2)大变异操作

当辨识结果出现局部收敛时，可采用大变异操作来解决这个问题，即当某一代中所有个体集中在一起时，就以一个远大于通常变异概率的概率执行一次变异操作，从而跳出局部最优，避免早熟［11］，但大变异是以牺牲收敛速度为代价的.

3)精英保留策略

大变异操作改变了收敛进程，增大了搜索的随机性，有可能破坏当前群体中适应度最好的个体，影响遗传算法的运行效率.为了加快优化速度，本文采用了精英保留策略，在父代个体中选择一个适应度最高的个体作为精英，与进化后子代适应度最高的个体相比较，如果前者大于后者，则用前者取代子代中最差的个体;反之，后者取代前者成为精英.

2.4 适应度函数的选择

在本文中，遗传算法的最佳适应度函数作如下表示:

式中:i为第i次采样.

即该问题的优化目标是使反作用飞轮的实际角动量与根据参数当前值估算得出的角动量之差的平方和最小.

3 参数辨识仿真

3.1 仿真过程

利用改进后的遗传算法对动力学参数辨识的过程如下:

1)种群内个体(染色体)选择为q，采用浮点数的形式对这些参数进行编码(浮点数编码比二进制编码及其他编码的计算效率和精度高);

2)定义各个动力学参数的小区间;

3)设定遗传算法的相关参数，如种群大小np，优化的最大代数nm，交叉概率pc，变异的概率pm，大变异的概率pmax和密集因子α等.这里，优化的代数ng连同适应度函数的容许精度etol共同控制遗传算法的结束;

4)令ng=1，在第2步所定义的小区间约束下，随机产生一个初始种群，其有np个个体;

5)计算每个个体的适应度函数值，且评价最佳个体的适应度函数值是否满足收敛精度的条件，如果满足则转到第13步，否则，继续下一步;

6)取适应度最高(适应度函数值最小)的个体作为精英;

7)基于每个个体的适应度值，分配其选择概率，从而完成子代的选择;

8)随机产生相配对个体和交叉点的位置，经交叉得到新个体;

9)将交叉后子代的最大适应度fmax与平均适应度favg比较，如果αfmax＜favg，则按大变异概率pmax对交叉后得到的个体进行变异操作得到新个体，否则用pm完成变异操作.

10)将所选择的精英与子代适应度值最高的个体相比较，如果前者大于后者，则用前者取代子代中最差的个体.

11)以新产生子代个体取代当前父代的个体，从而构成下一代;

12)令ng=ng+1，如果ng＞nm，则转到第13步，否则，转到第5步;

13)获得最佳适应度的个体，经解码得到需要的动力学参数.

3.2 输入条件

本文所研究的空间机器人系统如图2所示，由一飞行基座和6-DOF机械臂组成.

图2 空间机器人系统

其刚体固连坐标系如图3所示(图中所示为机械臂展开的情况，定义为关节处于零位的状态)，Zi为关节Ji的旋转方向.预先设定的名义动力学参数如表1所示，所设置的真实的动力学参数如表2所示.

表1 名义动力学参数

表2 真实动力学参数

图3 六关节空间机器人的构型

最后，作为约束条件，对动力学参数的辨识精度提出要求:参数误差百分比控制在10%.

3.3 基座与机械臂的轨迹规划

本文采用机械臂各关节分别单独激励的方法来完成对飞轮角动量的估算，规划方法均采用三次多项式插值法.所规划关节的输入条件如下:

1)驱动关节i(i=1～6)，其他关节经抱闸锁紧，作为一个刚体绕该驱动关节旋转;

2)驱动关节初始角和角速度θ0=˙θ0=0;

3)驱动关节末端角和角速度θf=θ，˙θf=0;

4)规划时间为10 s，采样时间为0.5 s.

取θ=π/6，则驱动关节的轨迹规划曲线如图4所示.

3.4 辨识结果

利用改进遗传算法，经仿真所获得的动力学参数辨识结果如表3所示;优化进程的适应度函数变化曲线如图5所示.由图5可知，仅经过600代，通过对28个待辨识动力学参数的调整，所优化的最佳适应度函数值达到0.013 7，取得了满意的优化效率和优化结果.在辨识中，如果平均适应度函数值与最佳适应度函数值较接近，则采取大变异操作，增大个体之间的差异，加快优化的进程;反之，如果平均适应度函数值与最佳适应度函数值差异较大，则采用通常的变异概率pm，保证由优化的稳定性.图5可看出，经过改进的遗传算法表现稳定，最佳适应度函数值随着代数的增加逐渐递减，而且趋势相比一般遗传算法较陡峭，证明其优化能力增强.如果最大遗传代数加大，则优化会继续进行，评价函数将进一步被优化，所辨识参数会更接近真实值.

图4 驱动关节规划曲线

根据表3，所辨识动力学参数的最大百分比误差(相对于真实动力学参数)为7.33%，最小百分比误差为0.006 52%，差别较大.总体而言，对飞轮角动量影响大的动力学参数辨识效果要好一些，影响弱的要差一些.然而，所辨识的参数均满足所提出的辨识精度要求，证明了上述算法具有强大的优化能力.

表3 改进遗传算法辨识参数的误差百分比

图5 适应度函数变化曲线

4 结论

1)本文基于空间机器人角动量守恒方程，通过六自由度机械臂的关节轨迹激励，计算名义动力学参数估算的飞轮角动量与实测角动量(在仿真中通过真实动力学参数计算)的差异，建立了遗传算法的适应度函数.

2)针对常规遗传算法容易出现“早熟”问题，本文采用小区间生成，大变异操作以及精英保留策略对其进行了改进.

3)仿真结果表明改进后的遗传算法能够有效避免局部收敛现象的发生，增加了动力学参数辨识的优化效率，取得了良好的辨识效果.

［1］SUJAN V A，DUBOWSKY S.An optimal information method for mobile manipulator dynamic parameter identification［J］.IEEE/ASME Transactions on Mechatronics，2003，2(2):215-225.

［2］LAMPARIELLO R，HIRZINGER G.Free-flying robots-inertial parameters identification and control strategies［C］//ESA Workshop on Advanced Space Technologies for Robotics and Automation(ASTRA 2000). Noordwijk，Netherland:［s n］，2000:1-8.

［3］GU Y，XU Y.A normal form augmentation approach to adaptive control of space robot systems［C］//Proceedings of the IEEE International Conference on Robotics and Automation.Atlanta，USA:［s n］，1993:731-737.

［4］XU Y，SHUM H，LEE J，et al.Space Robotics:Dynamics and control［M］.Deventer，Netherland:Kluwer Academic Publishings，1993:51-58.

［5］MUROTSU Y，SENDA K，OZAKI M.Parameter identification of unknown object handled by free-flying space robot［J］.Journal of Guidance，Control and Dynamics，1994，17(3):488-494.

［6］KATOH R，SAKON H，YAMAMOTO T.A control method for space manipulator mounted on a free-flying robot by using parameter identification［C］//Proceedings of the Asian-Pacific Vibration.Kitakyushu，Japan:［s n］，1993:1205-1209.

［7］ABIKO S，YOSHIDA K.On-line parameter identification of a payload handled by flexible based manipulator［C］//Proceedings of 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems.Sendai，Japan:［s n］，2004:2930-2935.

［8］YOSHIDA K，ABIKO S.Inertial parameter identification for a free-flying space robot［C］//Guidance，Navigation，and Control Conference and Exhibit.Monterey，USA:［s n］，2002:1-8.

［9］LAMPARIELLO R，HIRZINGER G.Modeling and experimental design for the on-orbit inertial parameter identification of free-flying space robots［C］//2005 International Design Engineering Technical Conference and Computers and Information in Engineering Conference.Long Beach，USA:［s n］，2005:1-10.

［10］何光彩，洪炳镕，郭恒业.基于参数辨识的冗余自由飞行空间机器人多臂协调运动规划［J］.宇航学报，2000，21(1):85-89.

［11］吕佳.大变异遗传算法在非线形系统参数估计中的应用［J］.重庆师范大学学报，2004，21(4):13-16.