灰色蚁群系统求解多目标卫星观测调度问题
王海波,徐敏强,王日新,李玉庆
(哈尔滨工业大学深空探测基础研究中心,哈尔滨150080,1021810103@163.com)
地球观测卫星的任务是根据用户需求获取指定区域的图像信息.为了能够最大限度的利用卫星资源,有必要对卫星的观测活动进行合理的规划和调度.由于卫星资源调度是一个典型的过载调度问题,在一定时间内不可能完成所有用户需求,这就需要根据成像需求的重要程度和云量信息,在满足侧视转换时间、存储容量等约束条件下,使尽可能重要、成像质量好的成像需求获得成像.目前,单颗卫星的观测调度以及多星联合观测调度问题,各国学者进行了大量研究,并取得了一定的成果[1-4].但是,国内外对该问题的研究很少系统地考虑云层覆盖对调度的影响,获得的图像可能因为云层的影响而得不到有效的使用,造成卫星资源的极大浪费.卫星观测调度问题已被证明是NP-hard问题,这意味着当问题规模很大时,不能在合理的时间内穷举出所有的成像路径.蚁群优化算法是一种元启发式算法,虽然不能保证得到的是最优解,但能在合理的时间内得到问题较好的近优解[5].因此,本文提出了一种灰色蚁群系统算法来解决卫星观测调度问题,采用多个目标函数评价成像路径的质量,实现观测数据高效优质的获取.
1 多目标卫星观测调度优化模型
1.1 基于区间灰数的云量描述
目前,主要通过两种方法得到无云或者少云图像:1)调度前利用云量预测模型进行成像预调度;2)调度后基于拍摄图像的云量评估进行重调度.合理的成像预测调度模型能有效降低重调度的成本,减少卫星资源的浪费.因此采用短期云量预报的卫星成像预调度,其调度时间段为6 h,关于重调度研究本文不作讨论.
云层覆盖是影响卫星拍摄图像质量最主要的因素.云量是有云天空占天空总面积的比例,我国云量计算单位采用10成制.天空无云,云量为0,天空完全为云所遮蔽,云量为10.由于现有的气象预报技术还不能准确地预测某地某时上空的云量,而往往给定一个云量信息的区间范围,因此本文采用区间灰数来描述卫星与成像需求观测时间窗口内的云量.灰数是指只知其大概范围而不知其确切值的数,通常用“⊗”表示.既有下界a又有上界¯a的灰数称为区间灰数,记为⊗∈[][6].
定义1 设⊗1∈,且记L(⊗1)=,则称p≥⊗(⊗12)=为⊗1≥⊗2的可能度[7].
在算法的每次迭代中,当蚁群系统中每只蚂蚁都构建一条完整的成像路径之后,通过区间灰数的运算法则以及区间数大小的可能度定义比较成像路径之间的云量大小.由于缺乏区间灰数取值的分布信息,采用等权均值白化得到每条成像路径的平均云量信息,进而得到Pareto最优解.
1.2 多目标卫星调度优化模型
卫星以一定的轨道绕地球运行,当卫星飞临目标区域时,由于受成像幅宽的限制,只能选取某个目标区域成像,而每个目标区域都有严格的观测时间窗口.由于卫星的姿态控制能力以及星上的存储容量有限,而且成像任务的观测时间窗口之间往往有重叠区域,一个轨道圈次内不能完成所有成像需求,需要考虑成像任务的重要程度、云量信息以及消耗的存储器容量等各种因素选择任务成像.在调度之前首先作如下假设:
1)一颗卫星任意时刻最多只能处理一个任务;
2)用户的成像需求为点目标,若为区域目标,可按照一定的规则分解为多个点目标;
3)任务在被执行期间不能被中断;
4)由于卫星沿着一定的轨道高速运行,在卫星与成像需求的可见时间窗口内,成像任务上空的云量不发生变化.
为了建立卫星成像调度问题模型,首先给出以下成像参数:调度的时间区间T;成像卫星集合S;待成像的任务集合J;卫星α对任务i的成像开始时间;卫星α对任务i的成像结束时间;成像任务i的持续时间di;卫星α对成像任务i的侧视角度aαi;成像任务i的权重因子pi;卫星α完成任务i所需的存储容量qαi;卫星α侧视角的转动速度rα;卫星α固态存储器的图像存储能力Mα;成像任务i与卫星α可见时间窗口内天空的云量[hαi,¯hαi];成像任务i允许的最大云量Hi;定义决策变量:γαi为二元变量,γαi=1表示卫星α调度成像任务i,否则γαi=0;bi表示任务i成像的开始时间;ωαik为二元变量,ωαik=1表示在卫星α的成像序列中,成像任务k与i相邻,且在i后执行,否则ωαik=0;
为了更全面的反映调度结果的质量,采用多目标函数评价成像路径,目标函数定义如下: 1)成像调度未完成成像任务的重要程度,

2)成像调度所有成像任务的平均云量,

成像调度过程中考虑的约束条件有:
1)初始成像任务的转换约束.虚拟初始任务0和该卫星所有可用任务都满足侧视约束,即

2)成像侧视角约束.卫星对一个任务成像之后,必须有足够的时间完成侧视动作,以对下一个任务成像,即

3)星上存储容量约束.卫星在成像任务过程中,存储的数据总量不能超过其最大容量,即

2 灰色蚁群系统的多目标优化算法
求解多目标优化问题的常用方法有字典排序法、目标加权法和基于Pareto最优解方法.前两种方法需要决策者已知目标函数的先验信息,而在卫星观测调度问题中,很难得到目标函数的相关信息.因此,本文采用基于Pareto最优解的思想,将Pareto前端分为多个相等部分,将蚁群也分为多个种群,每个种群搜索Pareto前端的一部分,搜索方向能覆盖整个解空间,且得到的Pareto最优解具有良好的分布性.为保证解的收敛性,采用精英保留策略,下面对算法的主要步骤作详细说明.
2.1 信息素的定义以及初始化
算法将“某个成像任务i被执行后立刻执行任务j的期望度”定义为信息素τij.对每个目标函数分别构建一个信息素矩阵,本文研究的成像调度模型包含两个目标函数,故可记为矩阵τ和τ',将这两个信息素矩阵中的所有元素值初始化为τ0.
2.2 解的构建
多种群策略能促进蚁群系统中子种群的生成和保持,从而保护一些次优解以维持种群多样性,防止蚁群系统收敛到Pareto前端的单一点.因此采用多种群搜索方式,将m只蚂蚁分为大小相等的m'个种群,每个种群中含有m″只蚂蚁,其中,m=m'×m″.每一代中,每只蚂蚁都构建一条完整的成像路径,在构建路径过程中,使用伪随机比例的状态转移规则选择下个成像任务,如下式所示:
如果q≤q0:
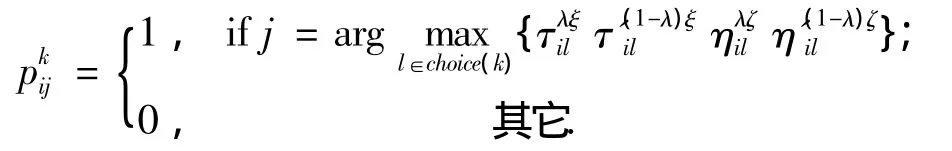
否则,
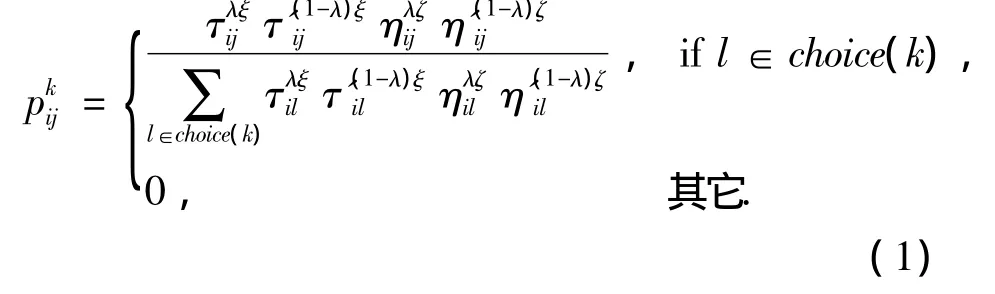
其中,q0∈[0,1],q是均匀分布在区间[0,1]中的一个随机变量,choicek表示第k只蚂蚁可选下一个成像任务的候选列表,候选列表是成像任务无圈有向图[8]上,与i相邻在i之后可成像的任务集合,可避免在成像任务i大规模的邻域上搜索,减小了搜索空间,节省了程序的运行时间.ξ和ζ分别是信息素和启发式信息的权参数.ηij和η'ij分别是边e(i,j)相对于每一个目标函数的启发式值,如式(2)(3)所示.

为加强每个种群的蚂蚁搜索Pareto前端不同的区域,每个种群都要由下式计算λ的范围,

其中:h∈{1,2,…,m'}.
2.3 精英保留策略
加会产生越来越多的优良个体,但由于状态转移规则的随机性,有可能破坏本属于Pareto前端的个体,影响蚁群系统的搜索效率和收敛性.精英保留策略的思想是在每个种群中,将当前Pareto前端的个体保留到下一代群体,参与信息素的更新操作.该策略可以明显加速蚁群算法的搜索过程,并且在找到优良解后可以防止它的丢失.因此,存储至今每个种群得到的Pareto最优解的成像路径Tbs,允许这些路径进行信息素的更新操作.
2.4 全局信息素更新规则
为了加强算法对Pareto前端各个部分的探索度,使用了一种区域更新规则,即每只蚂蚁只在它所属的种群中更新信息素矩阵.只有在当前迭代中得到的Pareto前端的路径Tis与该种群中至今最优路径Tbs才能释放信息素,且只有这些蚂蚁进行信息素的蒸发动作,如下式所示.

其中:

τ'信息素矩阵更新类似.
2.5 局部信息素更新规则
除了全局信息素更新规则外,灰色蚁群系统还使用了一个局部信息素更新规则如下式:

其中:参数ρl是局部信息素的蒸发速率,τ0是信息素的初始值.
在成像路径构建过程中,若蚂蚁经过边e(i,j),则调用这条规则更新该边上的信息素.
局部更新规则能增加蚂蚁探索未调度的成像任务的机会,使得算法不会陷入停滞状态.
3 仿真试验及结果分析
为了说明前文所建立的模型以及算法的有效性,对3颗太阳同步轨道地球观测卫星进行成像调度,假设卫星具有相同的轨道参数,如表1所示.星上CCD相机的侧摆能力为±32°,固态存储器容量274 Gb.所有任务的调度起止时间为2009-01-01T0/T6.
蚁群系统在进化过程中,虽然随迭代次数的增

表1 轨道参数
由于算法的参数较多,且各参数对算法的影响较大,因此采用多次试验比较的方式,最终确定各参数如表2所示时,运行结果较为理想.

表2 灰色蚁群系统的参数
为了对比算法的性能,应用多目标蚁群优化算法中广泛采用的Pareto ant colony optimization (PACO)[9]算法和本文提出的灰色蚁群系统优化(GACS)算法对500个成像需求进行调度,比较结果如图1所示.由图1可以看出,GACS得到的Pareto最优解支配大部分PACO算法求得的Pareto最优解,PACO算法虽然可以获得一定数目的最优解,但是获得的最优解数目较少,且分布性不如GACS均匀.两种算法的运行时间都满足运行时间限制,均不超过1 200 s.

图1 500个任务时算法的性能比较
为分析GACS算法的收敛性,用文献[10]中定义的信息熵来衡量式(1)中节点转移概率pkij的分布程度的信息量,熵值越趋近于0,表明节点转移规则更有确定性.所有节点熵值的平均值称为平均熵,平均熵随迭代次数变化情况如图2所示.

图2 GACS算法的收敛性分析
由图可知,随迭代次数的增加,平均熵值由初始的5.19逐步递减为1.90,表明当进化成熟时,非支配路径上的信息素浓度远大于支配路径上的信息素浓度,从而节点的概率分布也更稳定.
实际应用中,在得到卫星成像调度的Pareto最优解后需根据具体情况对这些成像序列进行选择,生成卫星的动作指令指导卫星完成成像任务.
4 结论
多目标卫星观测调度问题相比传统的卫星观测调度更符合实际的调度情况,也是新出现的一类复杂的问题.本文采用灰色蚁群系统对该问题进行了优化求解,仿真结果表明所建立的数学模型以及算法的可行性和合理性.
[1]BENSANA E,LEMAITRE M,VERFAILLIE G.Earth observation satellite management[J].Constraints,1999,4(3):293-299.
[2]WOLFE W J,SORENSEN S E.Three scheduling algorithms applied to the earth observing systems domain[J].Management Science,2000,46(1):148-168.
[3]LEMAITRE M,VERFAILLIE G,JOUHAUD F,et al.Selecting and scheduling observations of agile satellites[J]. Aerospace Science and Technology,2002,6:367-381.
[4]BIANCHESSI N,CORDEAU J,DESROSIERS J,et al. A heuristic for the multi-satellite,multi-orbit and multiuser management of Earth observation satellites[J].European Journal of Operational Research,2007,117 (2):750-762.
[5]DORIGO M,STUTZLE T.Ant colony optimization[M].Cambridge,MA:MIT Press,2004.
[6]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].第3版.北京:科学出版社,2004.
[7]王坚强,任世昶.基于期望值的灰色随机多准则决策方法[J].控制与决策,2009,24(1):39-43.
[8]GABREL V,VANDERPOOTEN D.Enumeration and interactive selection of efficient paths in a multiple criteria graph for scheduling an earth observing satellite[J]. European Journal of Operational Research,2002,139: 533-542.
[9]DOERNER K,GUTJAHR W,HARTL R,et al.Pareto ant colony optimization:A metaheuristic approach to multiobjective portfolio selection[J].Annals of Operations Research,2004,131:79-99.
[10]YIN PengYeng,WANG JingYu.Ant colony optimization for the nonlinear resource allocation problem[J]. Applied Mathematics and Computation,2006,174: 1438-1453.

