基于共享免疫粒子群算法的电力系统无功优化

李 宁,王林川,田 军

(东北电力大学,吉林吉林 132012)

基于共享免疫粒子群算法的电力系统无功优化

李 宁,王林川,田 军

(东北电力大学,吉林吉林 132012)

针对电力系统无功优化中的粒子群算法计算效率较低,而且易陷入局部最优解等问题,将共享免疫粒子群算法应用到无功优化中,该算法在进行初始化时,运用正交的思想,使得粒子分布均匀;并用记忆粒子和克隆选择来更新粒子,这样可以很好地保持优化过程中粒子群的多样性。经过算例计算证明,共享免疫粒子群算法与其他算法相比,能够及时跳出局部最优得到全局最优解,且收敛速度快、精度高。

无功优化;免疫粒子群算法;小生境;共享机制

0 引言

电力系统无功优化是指系统在一定运行方式下,使解向量满足各种约束条件并达到有功功率损耗、电压质量和无功补偿容量等预定目标综合最佳的优化问题,属于多约束非线性组合优化范畴[1]。近年来,随着优化技术的发展,出现了多种智能优化算法,如遗传算法GA(Genetic A lgorithm)、禁忌搜索法TS(Tabu Search)和粒子群算法PSO(Particle Swarm Optimization)等,虽然每种算法都较以前的经典算法有所改进,但是随着问题的规模和复杂程度越来越大,单一算法的性能逐渐受到局限,所以如何构造新的算法,在多个单一算法上取长补短,是提高算法优化性能的有效途径。

本文在前人研究的基础上,针对无功优化的特点,将共享免疫粒子群算法SIPSO(Sharing Imm unity Particle Swarm Op timization)应用到无功优化中,利用免疫算法中免疫系统的自我调节机制以及免疫记忆等功能,提高了算法的全局搜索能力,有效地克服了粒子群算法因为多样性的不足而造成的算法易陷于局部最优的缺点。

1 无功优化问题的数学模型

1.1 目标函数

以发电机机端电压、变压器变比和无功补偿容量为控制手段,以降低电网的有功网损为目标,无功优化问题的数学模型如下。

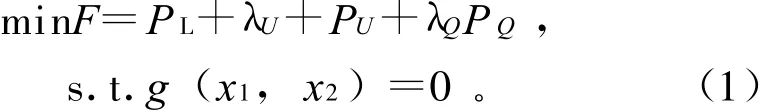
式中:PL——系统的有功功率损耗;

λU PU、λQPQ——分别为对 PQ节点电压越限和发电机无功越限的惩罚项;

λU、λQ ——分别为对节点电压和发电机无功越限的惩罚因子。

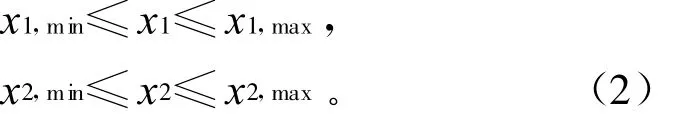
式 (2)中等式项表示系统的潮流约束方程、不等式项分别表示控制变量约束方程和状态变量约束方程。一般选取发电机端电压,无功补偿容量,可调变压器分接头为控制变量。而发电机无功出力和负荷节点电压为状态变量。网损和惩罚项的计算如式 (3)所示。

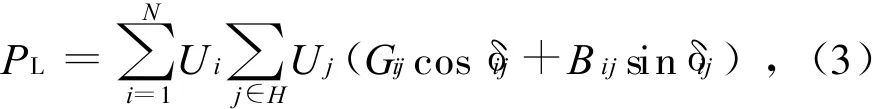
式中:N、N D和 N G——分别为系统节点、负荷节点和发电机节点总数;

2 免疫粒子群算法简介

2.1 基本粒子群优化算法

粒子群算法是一种基于集群智能的随机优化算法,每个优化问题的潜在解都认为是搜索空间中的一个粒子。算法首先初始化一群随机粒子,然后通过迭代找到最优解[2]。在迭代过程中,粒子根据2个极值来更新自己。第一个为粒子本身找到的最优解,称为个体极值,表示为p best;第二个极值为整个种群目前找到的最优解,称为全局极值,表示为g best。在D维搜索空间的位置表示为p i,相应的飞行速度为vi。在找到这两个最优值时,粒子i根据如下的公式来更新自己的速度和新的位置。

2.2 免疫粒子群算法

免疫粒子群算法是在原有粒子群算法的基础上,引入免疫算法的免疫信息处理机制进行改进,把抗体多样性和免疫记忆特性引入PSO,把粒子看作抗体,确保在保留适应度好的同时,能够保持记忆粒子的多样性,提高全局搜索能力[3]。为增加粒子的多样性,在每次迭代过程中通过以下2个方面产生新粒子:由粒子群算法的更新公式产生N个粒子;随机生成M个粒子。采用抗原与抗体的亲和力来描述可行解与最优解的逼近程度,亲和力高的个体所取得的目标函数值较好,同时,用抗体浓度表示与某抗体有较大亲和力的抗体数占整个抗体总数的比例。抗体与抗原的亲和力通过式 (10)来计算。

3 采用改进免疫粒子群算法求解无功优化问题

3.1 产生初始抗体种群

对于粒子群初始位置,在现在的无功优化研究中,大多普遍采用的是随机生成的方法,这样对于多峰函数就有可能存在盲区而不被搜索到。所以为了避免这种情况,本文采用正交化设计的方法来设置粒子的初始位置。具体方法是:将可行解空间量化为N个水平,并且分成N个子空间,在每一个子空间内随机生成一个粒子。这样就使得粒子均匀地分布在各个区域,有利于全局搜索。

3.2 抗体和抗原的识别

求解问题的目标函数对应为入侵生命体的抗原,将问题的解对应为免疫系统产生的抗体。在解决实际问题时,目标函数和约束条件作为抗原输入,随后产生初始抗体群,通过一系列遗传操作及抗体亲和度的计算,在保持抗体多样性的情况下找出抗体种群中与抗原亲和力最大的抗体,即为问题的解。

3.3 引进共享免疫机制

共享机制算法是一种共享适应度小生境实现方法。生物学上,小生境指生物在进化的过程中,一般总是与自己相同的物种生活在一起,繁衍后代,同种生物之间又相互竞争,同时不同种群的生物之间还存在相互的信息交换。针对PSO在进化后期由于种群多样性变差引起搜索效率降低的缺点,将共享机制算法中的共享函数在群体多样性变差时引入,抑制浓度较高的粒子,但其中最优的个体并不受抑制的影响,这样既增强了群体的多样性同时又保存了群体中最好的粒子。原粒子的适应度按式(11)、式 (12)更新为共享适应度F[4]。

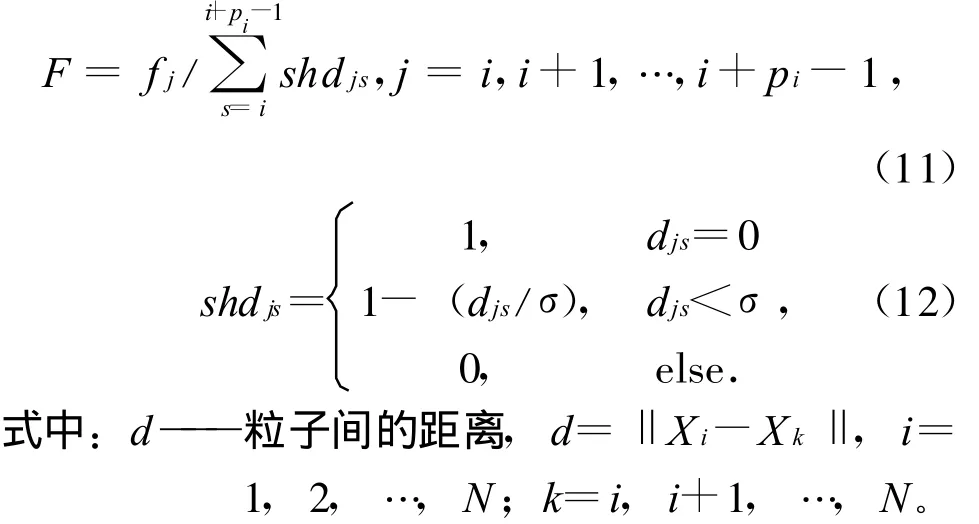
具体做法是:先将初始粒子按式 (8)和式(9)进行进化,当全局最好解连续进化若干代无变化时,这时可以认为进化陷于局部最优,此时停止进化而对粒子进行更新。更新粒子的产生借鉴免疫机制中的免疫记忆特性和克隆选择算子。用如下的共享机制算法产生记忆粒子。

a)置i=1。

b)计算粒子间的距离d。根据d＜σ,确定小生境子种群M p,p为子种群的元素个数。

c)如果小生境子种群Mp中包含群体中适应度值最好的粒子,则保存其中一个最好适应度值的粒子;否则,其余个体按步骤d)更新适应值。

d)根据式 (11)计算小生境子种群中个体的更新适应值 (即共享适应值)。

e)利用更新适应度值F及处罚函数对子群中高适应的个体进行处罚,即当种群中某个体不满足进化要求的时,比较此个体与更新适应度值粒子的适应值,并对其中的适应度值较高的粒子进行处罚,使其达到进化要求。

f)若i+p＜N,令i+p趋近于i,返回步骤b);否则,进入下一步。

g)按一定的选择率进行克隆,选出亲和力高的抗体。

h)对更新后的粒子继续按原进化方程进行进化,直到达到终止条件,即达到最大迭代次数并且获得的最优个体是问题的可行解,终止。

3.4 算法步骤

免疫粒子群算法充分结合了粒子群算法和免疫算法的优点,大大提高了算法效率,有利于更好地进行电力系统无功优化。算法的步骤如下。

a)系统初始化,给出算法的初始值。

b)通过正交化设计的方法均匀分布的初始抗体种群。

c)对上述群体中的各抗体 (粒子)进行评价,包括初始种群的适应度、抗体之间的亲和力、抗体与抗原间的亲和力及抗体的浓度。

d)形成父代种群,对粒子的位置和速度进行进化。

e)当全局极值连续进化若干代仍没有变化,而又未达到终止条件时,停止进化,按共享免疫机制产生记忆粒子。

f)克隆选择,继续对更新后的粒子对其进行速度和位置的进化。

g)如未达到终止条件,返回步骤b);否则终止。

4 算例分析

以IEEE-30节点系统作为测试用例,对基于共享免疫粒子群算法进行验证。测试系统的部分数据如表1所示,该系统包含6个发电机节点即:1、2、5、8、11和 13节点 (节点 1为平衡节点,其余为PU节点);22个PQ节点 (节点11和24是无功补偿点,调节步长为0.048);41条支路 (支路6-9、6-10、4-12和27-28为变压器支路,调节步长为0.012 5);变压器和并联电容器的档数均设为10档,系统的初始网损耗为0.083 24 p.u.。系统的其他支路参数和节点参数请见文献 [5,6]。

表1 测试系统部分数据

为验证SIPSO的有效性,分别采用标准粒子群算法和禁忌粒子群算法与共享免疫粒子群算法进行无功优化计算与比较。算法的参数设置如下:在禁忌粒子群算法[7]中,种群数目为50,TS的邻域解和候选解均取8个,禁忌表长为6,记忆长度为100,频率限度取40,局部最优解集长度取4,终止判据取最大迭代次数100。PSO算法和本文算法为:种群数目为50,学习因子取2.05,惯性权值的起始值和终止值以及最大迭代次数分别为0.9、0.4和100,记忆细胞数量为20。

由表2可以看出SIPSO相比于PSO算法和禁忌粒子群算法具有如下优点。

a)几种方法所得到的有功网损均有所下降,但是,基于共享免疫粒子群算法平均网损的下降率却比标准粒子群和禁忌粒子群算法分别高出9.26和6.22个百分点,这是采用正交化设计的方法来设置粒子的初始位置,而非随机选取,其陷入局部最优解的可能性减小,寻找到最优解的几率更高,优化结果在3种算法中最好正是其算法优越真实反应,因此得到了更好的优化结果。

b)由表2可以看出,SIPSO能收敛于较好的解,显示了基于浓度的选择机制保持群体的多样性的信息处理机制的有效性和优越性;同时,可以看出该算法下降速度很快,在迭代27次左右就已经接近最优解,这是因为在进化后期,共享免疫机制的引入提高了进化后期的寻优能力,提高了算法的收敛速度,所以这是一种令人满意的计算方法。

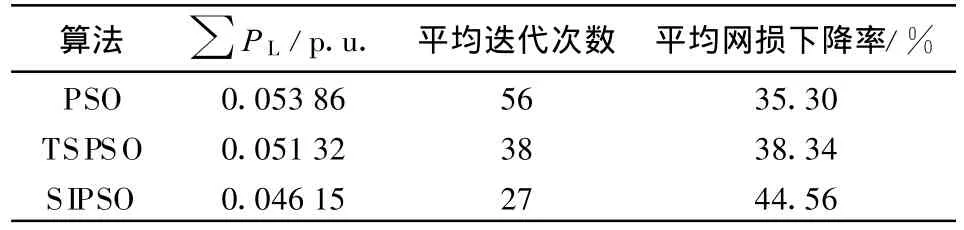
表2 3种算法的优化结果比较

5 结论

尝试将共享免疫粒子群算法用于求解无功优化问题,算例计算表明该算法能够以较少的种群规模更准确地收敛到全局最优解,有很好的计算效率和收敛稳定性,所以该方法是可行的、有效的。在无功优化过程中,利用正交化方法设定粒子的初始位置,根据抗体与抗原的浓度进行免疫选择策略保留优良粒子,很好地保持了群体多样性,同时防止了算法优化性能退化。另外,由于基于共享免疫粒子群算法是混合算法,在进行电力系统网络重构时随着系统规模的增大,其计算时间也会相应地增加,但随着计算机计算速度的提高,以基于共享免疫粒子群算法将在电力系统中具有更广阔的前景。

[1] 张勇军,任震,李邦峰.电力系统无功优化调度研究综述[J].电网技术,2005,29(2):50-56.

[2] 赵波,曹一家.电力系统无功优化的多智能粒子群优化算法[J].中国电机工程学报,2005,25(5):1-7.

[3] 李莉,李洪奇,谢绍龙,等.基于克隆选择的免疫粒子群优化算法 [J].计算机科学,2008,35(10):254-278.

[4] 胡春霞,曹建潮.共享免疫微粒群算法[J].系统仿真学报,2008,20(16):4278-4280.

[5] 聂宏展,张冰冰,王新.基于改进粒子群算法的电力市场下的无功优化 [J].电网技术,2007,31(21):85-90.

[6] 田康,张尧,郭力,等.基于家族优生学进化算法的电力系统动态无功优化[J].电网技术,2007,31(7):6-11.

[7] 黄玮,林知明,李波.基于禁忌搜索粒子群算法的无功优化[J].电力学报,2007,22(4):443-446.

Reactive Power Optim ization on Sharing Immunity Particle Swarm Algorithm in Electric Power System

LINing,WANG Lin-chuan,TIAN Jun
(Northeast DianliUniversity,Jilin,Jilin 132012,China)

It is applied of the sharing immunity particle swarm algorithm in reactive pow er optim ization due to the low efficiency and lim ited partialoptimum solution of particle sw arm optimization(PSO)in elec tric power system.Orthogonal princip le is app lied in the initialization of the algorithm,tomake particles evenly distributed and renewed by memory particles and clone choice,and to keep the diversity of particles sw arm during the optim ization process.It is proved based on calculation that compared with other PSO algorithms,the proposed Sharing Immunity Particle Swarm Op tim ization algorithm shallachieve the w hole op timum so lution with high convergence speed and accuracy in stead of lim ited partial op timum so lution.

reactive pow er optim ization;immunity particle sw arm optimization;niche;sharing mechanism

TM 761+.1

A

1671-0320(2010)01-0031-04

2009-07-15,

2009-12-12

李 宁 (1982-),男,吉林德惠人,东北电力大学电气工程学院2007级硕士研究生,主要研究方向为电力系统无功优化;

王林川 (1955-),男,四川潼南人,1982年毕业于东北电力大学电力系统自动化专业,教授,主要研究方向为电力系统运行分析;

田 军 (1982-),男,黑龙江虎林人,东北电力大学电气工程学院2007级硕士研究生,主要研究方向为电网的稳定与控制。