含错m序列本原多项式的高阶统计测定算法

苏绍璟，伍文君，黄芝平，刘纯武

(国防科技大学 机电工程与自动化学院，湖南 长沙410073)

0 引言

m 序列在通信领域中有着广泛应用。如在SDH 通信系统中，m 序列用来对数据流进行扰码处理，以增强数据的随机性，便于时钟恢复以及增强通信的保密性;在扩频通信中，m 序列也是应用最广泛的扩频码序列。因此，有必要研究如何检测与恢复m 序列。

国内外一些学者对m 序列的检测进行了探讨。Adams，Peter 等［1-4］提出高阶统计的方法对m 序列进行检测，并提到根据高阶统计函数峰值的位置可以测定m 序列的本原多项式。文献［5］也研究了基于高阶统计的m 序列检测，提出了基于偏三阶相关函数峰值特性的m 序列的检测方法和识别标准，证明偏TCF 具有与三阶相关函数所对应截取区域相同的峰值特性，根据这一特性可以对m 序列进行检测及识别。

现有文献的研究重点是m 序列的检测，而对m序列的本原多项式的测定研究的并不深入。Adams等提到可以通过计算峰值位置的重复性来确定m序列的本原多项式。但该方法在本原多项式的阶数较高，而截断的序列长度有限的情况下，并不适用，且计算量很大。实际中常用的测定本原多项式的方法是Walsh 变换法［6］。但该方法的性能受制于本原多项式的抽头数，且当截断序列长度一定，而误码率增加时，其能准确测定的概率将显著降低。为了克服Walsh 变换法的这一不足，本文在Adams 等的研究成果的基础上，利用概率分析，深入研究了基于高阶统计原理的本原多项式测定算法。新算法克服Walsh 变换法性能受制于本原多项式抽头数的影响，但计算复杂度相对更高。

1 m 序列及高阶统计原理

1.1 m 序列的产生与性质

m 序列是最大周期线性反馈移位寄存器序列。图1为生成线性反馈移位寄存器序列的原理图。从图中可以看出，线性反馈移位寄存器序列由寄存器的抽头系数及寄存器的初始状态决定。设序列的生成多项式为

f(x)的多项式系数对应于反馈移位寄存器的抽头系数。因此f(x)就确定了线性反馈移位寄存器的结构。当f(x)为二元域上本原多项式时，其生成的序列具有最大周期，也就是m 序列。

图1 线性反馈移位寄存器原理图Fig.1 Schematic of liner feedback shift register

m 序列具有一些优良特性:

1)平衡性:m 序列中一个周期内“1”的数目比“0”的数目多1 个。

2)平移相加性:m 序列与其移位后的序列逐位模2 相加后，所得序列仍然是一m 序列，只是相移不同而已。

3)二值相关性:m 序列具有优良的二值自相关特性，码位数越长越接近于随机噪声的自相关特性。但是，2 个相同长度的m 序列的互相关特性并不是很好。

1.2 高阶统计原理

以3 阶统计为例进行介绍高阶统计原理。m 序列的3 阶相关函数(triple correlation function，TCF)定义为

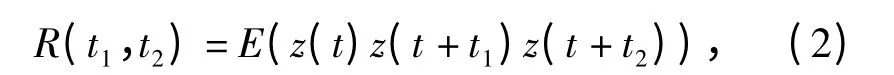
式中:R(t1，t2)为3 阶相关函数;z(t)为m 序列;t1，t2=1，2，…，L -1，L 为序列的周期。实际分析中，z(t)由±1 组成，而不是0，1，对应关系如下:(0，1)→(1，-1).故式(2)中的乘法，其实就是模2加。3 阶相关值在实际中由下式近似计算

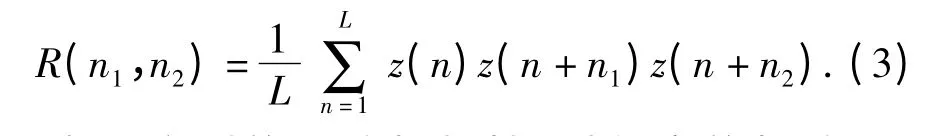
由m 序列的平移相加性，对任意的相移n1，z(n)z(n+n1)仍是m 序列。假设得到的m 序列相对原序列的相移为n2，则∀n，z(n)z(n +n1)z(n +n2)=1，此时，R(n1，n2)=1.而对于不满足上述的条件的n1，n2，z(n)z(n +n1)z(n +n2)也仍然是m序列。由m 序列的平衡性可知，在m 序列的一个周期内，”1”的数目比”0”的数目多1.因此，此时R(n1，n2)=-1/L.所以，m 序列的TCF 为

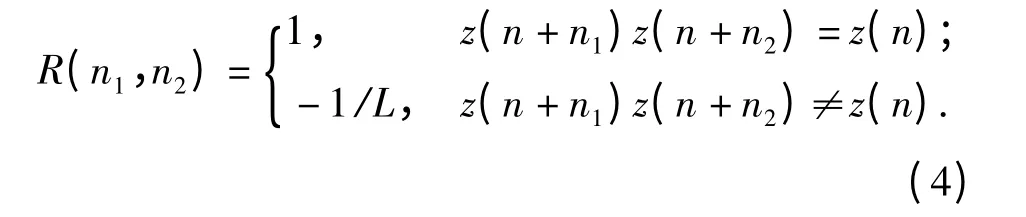
因此，m 序列的平移相加性导致m 序列的TCF有峰值出现。根据这一特点，就可以通过计算3 阶相关值来检测m 序列。更高阶的相关统计同样存在这样的特征。

实际上，大多数情况下我们并不知道m 序列的周期长度，而且，通常截取的m 序列长度小于m 序列的周期长度，那么，截取的这一部分m 序列的TCF 是否能体现m 序列的TCF 的峰值特性呢?文献［5］说明这是可能的，并提出了偏3 阶相关函数(偏TCF)的概念，定义如下

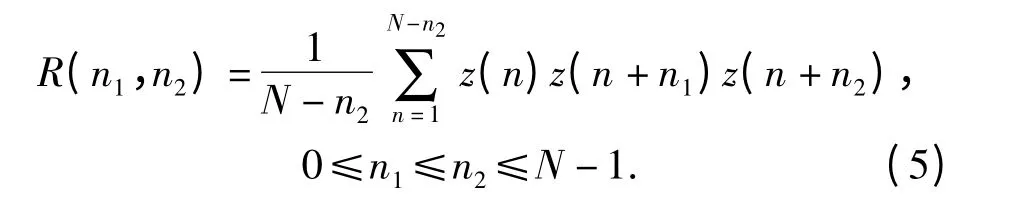
式中，N 为截取的序列长度。按照式(5)计算得到的1～N 区间的TCF 峰值位置与按照整个序列周期长度计算的TCF 相对应的局部区域的峰值位置是一致的。

2 基于高阶统计的本原多项式测定

2.1 基本思路

令z(n)(0≤n＜N)为m 序列，f(x)为其本原多项式，其阶数为l，截断序列长度为N.计算该序列的偏d 阶相关函数

若R 在某位置(s1，s2，…，sd-1)出现峰值，则有

观察上式可知，多项式g(x)=1 + xs1+ xs2+…+xsd-1的反转多项式g'(x)符合m 序列z(n).由m 序列的基本理论可知，f(x)整除g'(x)，也即f(x)是g'(x)的一个因式。这样，若能找到R 的几个峰值，通过求这几个峰值位置对应多项式的最大公约式，就能测定该序列的本原多项式。

在实际应用中，得到的截断m 序列的长度通常要远小于该序列的周期。此时，序列高阶相关函数并不一定存在峰值。例如，对于本原多项式f(x)=x17+x15+x14+x13+x11+x10+x9+x8+x6+x5+x4+x2+1，截断序列长度N=400，其3 阶相关函数并不存在峰值，而只有更高阶的相关函数才存在峰值。因此，我们有必要对m 序列的高阶相关函数的峰值分布进行研究。

文献［7］提到，由于m 序列具有很好的伪随机特性，假定其高阶相关函数峰值也平均分布，则

式中，m(d)为d 阶相关函数峰值数的估计值。文献［7］还以本原多项式f1(x)=x17+x3+1 及f2(x)=x17+x15+x14+x13+x11+x10+x9+x8+x6+x5+x4+x2+1 做了仿真实验，实验结果见表1［7］.实验表明这个公式是合理的。该公式也是本文算法的基本假设之一。

表1 式(8)估计值与实际值对比Tab.1 The comparison between approximate value with Function (8)and actual value

有了上述假设，我们就可以设计算法了。设有含错m 序列z(n)(0≤n＜N)，N 为序列长度，误码率为p.∀(n1，n2，…，nd-1)，(1＜n1＜n2＜…＜nd-1＜N1)，计算其d 阶相关函数

式中，N1为向量(n1，n2，…，nd-1)对应多项式的最高阶数，N2为统计次数，显然N1+N2≤N.搜索R(n1，n2，…，nd-1)的峰值，通过求解这些峰值位置所对应的多项式的最大公约式，就可以导出该序列的本原多项式了。

2.2 参数选取

式(9)中有3 个参数需要确定:相关函数阶数d，多项式最高阶数N1以及统计次数N2.下面分别讨论它们的选取。首先对于特定相关函数阶数d，N1的选取至少应满足m(d)≥2，当m(d)=2 时，得到的最大公约式仍然可能为本原多项式的倍式。实践中发现，当m(d)≥4 时，得到的最大公约式通常为所求的本原多项式。另外考虑到误码率较大时，峰值位置可能出错或不能得到，本算法暂取m(d)≥10.故:

N2的选取应满足在高误码率情况下，也能将部分d 阶相关函数R 的峰值区分出来。对于含错m序列，由puling-up 定理［8］可知，式z(n)z(n+n1)z(n+n2)…z(n+nd-1)成立概率s 为

式中，ε=1/2 -p.这样，当向量(n1，n2，…，nd-1)处于R 的峰值位置时，Pr(z(n)z(n +n1)z(n +n2)…z(n+nd-1)=1)=s.而对于非峰值位置的向量(n'1，n'2，…，n'd-1)，由m 序列的伪随机特性，有Pr(z(n)z(n+n'1)z(n +n'2)…z(n +n'd-1)=1)=0.5.假设∀n，z(n)z(n +n1)z(n +n2)…z(n +nd-1)相互独立，则R(n1，n2，…，nd-1)可以看成N2次伯努利试验。由De Moivre-Laplace 中心极限定理，当N2较大时，R(n1，n2，…，nd-1)渐进于正态分布。

对处于峰值位置的向量(n1，n2，…，nd-1)，有E(z(n)z(n+n1)z(n +n2)…z(n +nd-1))=2s -1，D(z(n)z(n+n1)z(n+n2)…z(n +nd-1))=4s(1 -s)，则

而对于其他向量(n'1，n'2，…，n'd-1)，有E(z(n)z(n+n'1)z(n+n'2)…z(n+n'd-1))=0，D(z(n)z(n +n'1)z(n+n'2)…z(n+n'd-1))=1.则

考察式(12)及式(13)可以发现，当误码率p 越大时，s 趋近于0.5，此时峰值位置与非峰值位置的期望差越小，也就是两者的概率空间重叠部分越多，峰值就越难区分出来。另一方面，N2越大，两者的方差越小，此时概率空间重叠越小，峰值就更容易区分。图2，3 反映了这一过程。图2，3 为误码率p =0.25，N2分别为300 和800 时，峰值位置的了概率分布与非峰值的R(n1，n2，…，nd-1)概率分布情况。

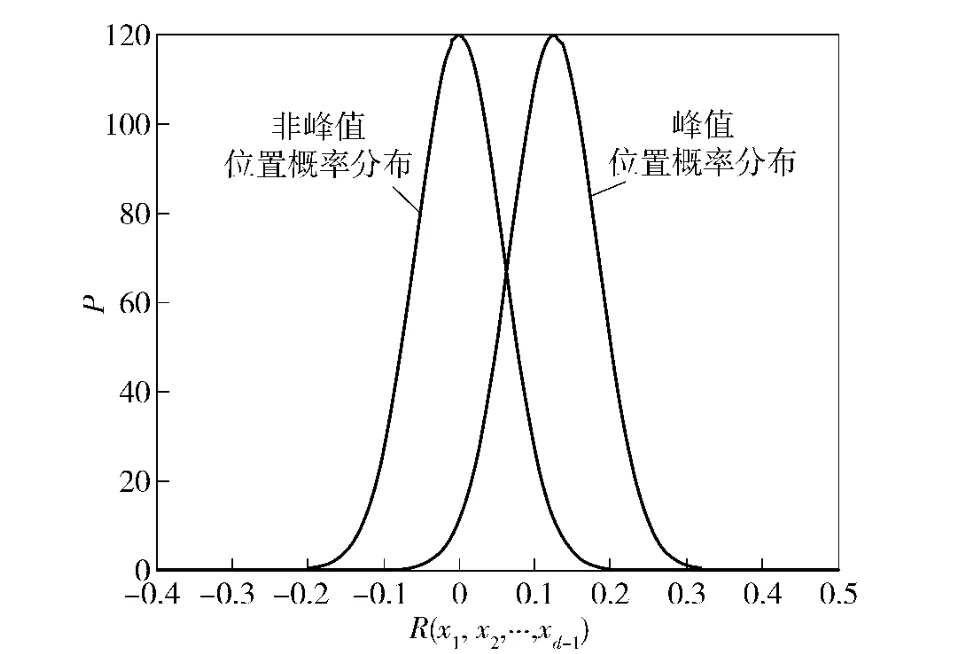
图2 p=0.25，N2 =300 时，R(n1，n2，…，nd-1)概率分布Fig.2 The probability distribution of R(n1，n2，…，nd-1)when p=0.25 and N2 =300

由以上分析可知，对于特定的p 与d，N2的取值决定了是否能区分峰值。设定阈值h，当R(n1，n2，…，nd-1)＞h 时，我们认为这个值为d 阶相关函数的峰值。h 应使非峰值被误认为峰值的平均数目小于1，这样我们就最多可能得到一个错误的峰值，有

另外，h 还应满足使大多数的峰值能区分出来。由于计算Pr(R(n1，n2，…，nd-1)＞h)的解析式较为复杂，为了简化计算，我们取h 小于峰值位置R(n1，n2，…，nd-1)的期望值，即

图3 p=0.25，N2 =800 时，R(n1，n2，…，nd-1)概率分布Fig.3 The probability disribution of R(n1，n2，…，nd-1)when p=0.25 and N2 =800

综合式(14)和式(15)，我们就能确定参数N2.

现在，我们可以说明之前为什么选择m(d)≥10.由式(15)可知，峰值被找到的概率大于0.5，这样，很容易算得:从10 个峰值中找出3 个峰值的概率就大于0.95.因此，选择m(d)≥10，使得我们至少能找到3 个峰值，以推导出本原多项式。

相关函数的阶数d 是需要探讨的另一个重要的参数。式(10)表明，峰值的数量m 随着d 的增长而增长。当截断m 序列的长度远低于序列周期时，可以通过增加d 以找到算法成功所需的峰值数。然而，另一方面，式(11)也表明，d 的增加将导致s 的降低。而由式(15)，s 的降低将导致N2的急剧增加，并可能使得N2＞N，算法失败。由以上分析可知，d，N1和N2这3 个参数是相互联系，相互制约的，需要综合权衡才能确定它们的最佳取值。在本算法中，初始化d=3，当算得N1＞N 时，再增加d 重新再算，直到N1＜N.

2.3 算法步骤

有了以上的这些探讨，下面给出新算法的完整步骤:

1)通过观察m 序列的游程，估计本原多项式的阶数l.初始化d=3，由式(10)计算N1.如果N1＞N，则更新d =d +1，并重新计算N1.重复这一步骤直到N1＜N.

2)估计序列的误码率为p，由式(14)、式(15)并查正态分布表，确定阈值h 和N2.如果N1+N2≥N，则转步骤5.

3)∀(n1，n2，…，nd-1)，0≤n1≤n2≤…≤nd-1＜N1，计算其d 阶相关函数R(n1，n2，…，nd-1)，当R(n1，n2，…，nd-1)＞h，储存该向量(n1，n2，…，nd-1).如果找到了4 个峰值，则转到步骤4.a，如果只找到了3 个峰值，则转步骤4.b，否则转步骤5.

4)求解储存向量(n1，n2，…，nd-1)所对应的反转多项式(1 +xn1+xn2+…+xnd-1)'的最大公约式。

a.如果算得的最大公约式不为1，则认为该最大公约式就是序列的本原多项式。如果其中一个多项式与其他多项式互素，则认为该多项式是错误的，重新计算其他多项式的最大公约式，如果这个最大公约式不为1，则同样认为该最大公约式就是序列的最大公约式。否则，转步骤5.

b.如果算得的最大公约式不为1，则该最大公约式即为序列的本原多项式，否则转步骤5.

5)未能测得序列的本原多项式，算法失败。

3 仿真计算及性能分析

3.1 仿真计算

使用Matlab 软件，在Pentium4 2.8 G 机器上进行了大量的仿真计算。例如，以f(x)=x17+ x15+x14+x13+x11+x10+x9+x8+x6+x5+x4+x2+1 为本原多项式，误码率0.25，生成截断序列长度10 000的含错m 序列。首先通过观察含错序列的游程，估计其本原多项式阶数l 为20.令d =3，由式(10)算得N1=4 096.由式(14)、式(15)及查正态分布表，算得h =0.125 和N2=1 600.穷举所有向量(n1，n2)，0≤n1≤n2＜N1，计算其3 阶相关函数R(n1，n2)，储存R(n1，n2)≥h =0.125 的向量。这样，我们得到(130，1258)，(210，813)，(278，1543)和(216，483)，其对应的反转多项式分别是x1258+x1127+1，x813+x602+1，x1543+x1264+1 及x483 +x266 +1，它们的最大公约式便是其本原多项式f(x).上述过程耗时约35 s.由于每次仿真找到的峰值位置都不相同，计算时间也就不同。在上面这个例子中，计算时间大约在15～60 s 之间。

3.2 计算复杂度分析

计算新算法的计算复杂度。在最坏的情况下，新算法需要穷举所有可能的向量(n1，n2，…，nd-1)，0≤n1≤n2≤…≤nd-1＜N1，总共有个向量。由式(10)，有Nd-11/(d -1)!=10 ×2l，所以总共有10 ×2l个向量。对于每个向量都需要做N2次运算，因此新算法的计算复杂度为o(2lN2).相比Walsh 变换法的计算复杂度o(2ll))［6］，新算法的计算复杂度要更高。在实际应用中，通常并不需要穷举所有可能的向量，因此计算时间通常要远小于最坏情况下的计算时间。

3.3 算法成功概率分析

Walsh 变换法成功测定本原多项式的概率与本原多项式的抽头数相关，本原多项式的抽头数越多，其成功测定的概率越低。在上一小节的例子中，Walsh 变换法就未能成功找到本原多项式，但如果将f(x)=x17+x3+1 替代上例使用的本原多项式，则Walsh 变换法也能成功求出本原多项式。由此可见，新算法的性能与本原多项式的抽头数无关。

为进一步考察新算法的性能，分别以C1(x)=x17+x3+1 和C2(x)=x17+ x15+ x14+ x13+ x11+x10+x9+x8+x6+x5+x4+x2+1 为生成多项式，在不同的误码率及不同的截断序列长度情况下做了大量的仿真试验。图4和图5分别给出了生成多项式为C1(x)和C2(x)时，在不同的误码率下，Walsh 变换法和新算法能成功测定生成多项式的概率。图中截断序列长度分别为20 000 和80 000，算法成功概率值为随机试验500 次得到的估计值。从图中可以看出，当生成多项式的抽头数为2 时，Walsh 变换法和新算法的容错性能相当，但随着生成多项式抽头数的增加，Walsh 变换法的容错能力急剧降低，而新算法的容错性能不随生成多项式抽头数的增加而降低。此外，截断序列长度越长，相同误码率下，算法成功的概率越高。

图4 新算法与Walsh 算法容错能力对比(生成多项式抽头数为2)Fig.4 The error tolerance ability comparison between the new algorithm and the Walsh-Hadamard transformation when the number of tap is 2

由以上对新算法的性能分析可知:相比实际中常用的Walsh 变换法，新算法克服了其性能受制本原多项式抽头数的不足，并且在本原多项式阶数为17，截断序列长度为50 000 及误码率达到0.36 的情况下，依然可以算得正确的本原多项式，体现出了很好的容错能力。新算法不足之处在于，算法的计算复杂度相对较高。

图5 新算法与Walsh 算法容错能力对比(生成多项式抽头数为12)Fig.5 The error tolerance ability comparison between the new algorithm and the Walsh-Hadamard transformation when the number of tap is 12

4 小结

实际中常用Walsh 变换法［6］来测定m 序列的本原多项式，但是该方法的性能受制于本原多项式的抽头数。当本原多项式的阶数较高时，其抽头数也往往较多，这时Walsh 变换法常常无法得到本原多项式。本文基于这点考虑，对基于高阶统计的m序列本原多项式测定做了深入的研究。本文给出了基于高阶统计的m 序列本原多项式测定的基本思路，详细探讨了各个参数的确定方法，并给出算法的完整步骤。该算法与常用的Walsh 变换法相比，性能不再受制于本原多项式的抽头数，且具有很好的容错能力。新算法不足之处在于，计算复杂度相对较高。

References)

［1］Adams E R，Gouda M，Hill P C J.Detection ＆characterisation of DS/SS signals using higher-order correlation［C］∥Proc IEEE ISSSTA’96.Mainz，1996:7 -31.

［2］Batty K E，Adams E R.Detection and blind identification of msequence codes using higher order statistics［C］∥Proceedings of IEEE on Signal Processing Workshop，Caesarea.1999:16 -20.

［3］Adams E R，Gouda M，Hill P C J.Statistical techniques for blind detection ＆ discrimination of m-sequence codes in DS/SS systems［C］∥Proc IEEE 5th ISSSTA symposium’98.Sun City，1998:853 -857.

［4］Adams E R，Hill P C J.Detection of direct sequence spread spectrum signals using higher-order statistical processing［C］∥Proc Int.Conference on Acoustics Speech and Signal Processing，ICASSP’97.Munich，1997:3849 -3852.

［5］俎云霄.基于高阶统计处理技术的m-序列检测及识别［J］.电子与信息学报，2007，29(7):1576 -1579.ZU Yun-xiao.The detection and recognition of m-sequence using higher-order statistical processing［J］.Journal of Electronics and Information Technology，2007，29(7):1576 -1579.(in Chinese)

［6］游凌，朱中梁.Walsh 函数在解二元域方程组上的应用［J］.信号处理，2000，16:27 -30.YOU Ling，ZHU Zhong-liang.The application of walsh function in resolving of F(2)equations［J］.Signal Processing(chinese)，2000，16:27 -30.(in Chinese)

［7］Canteaut A，Trabbia M.Improved fast correlation attacks using parity-check equations of weight 4 and 5［G］∥Bart Preneel，Advances in Cryptology-EUROCRYPT 2000 LNCS.Germany:Springer，2000，1807:573 -588.

［8］Matsui M.Linear cryptanalysis method for DES cipher［G］∥Tor Helleseth，Advances in Cryptology-EUROCRYPT 1993.LNCS.Germany:Springer，1994，765:386 -397.