一种对称三角线性调频连续波雷达的校正算法

侯志，缪晨，吴文，张铎

(南京理工大学 近程高速目标探测技术国防重点学科实验室，江苏 南京210094)

0 引言

线性调频连续波(LFMCW)雷达具有低截获概率，无距离盲区等优点，在海军战术导航雷达，近程防御和汽车防撞雷达等多个领域得到了广泛应用［1］。在近程防御中，如何在复杂环境中准确的检测目标，提取目标的距离速度方位信息，对目标进行实时跟踪已经成为国内外的研究重点。

目前，LFMCW 雷达回波中频信号的处理普遍采用差拍傅立叶变换方法。文献［1］提出锯齿波调制信号的距离维FFT 变换测距和MTD-多普勒滤波器组测速方法，文献［2］提出锯齿波调制信号的二维FFT 变换测距测速方法［2］，文献［3］提出对称三角波调制信号的动目标检测和频域配对相结合的方法［3］，都用到了FFT 变换。在实际的信号处理中，FFT 变换的分辨率和栅栏效应会对系统测速测距精度造成影响，主要表现在两个方面:1)FFT 变换栅栏效应的固有频率间隔引入测距测速误差。2)当目标多普勒频率较小时，无法消除运动目标的距离速度耦合现象而引入的测距误差。因此对LFMCW 雷达回波处理结果进行频域校正成为提高测距测速精度的必要手段。

本文在A G Stove、A Wojtkiewicz、T Grandke 等人研究的基础上，结合近程防御雷达的特点提出了一种频域校正方法，该方法将对称三角波调制信号的二维FFT 信号处理算法与频率校正算法相结合，消除多普勒频率不敏感目标的距离速度耦合，提高系统的测量精度。

1 LFMCW 雷达测距测速算法分析

1.1 LFMCW 雷达二维FFT 信号处理算法

对称三角波调制LFMCW 雷达发射信号为

其中:Vcm为可归一化幅度;μ =2B/T 为对称三角波的调频斜率;B 为调制带宽;T 为三角波周期;φ0为初始相位。假定指向雷达接收机方向为速度的正方向，一个径向速度为v0，距离为R0的点目标的回波延迟为τ(t)=2(R0-v0t)/c，考虑多周期情况时tk=t-kT，目标在不同调制周期k 时的回波延时可写为τ(tk)=2(R0-v0t+vkT)/c，因此上扫频段的不同调制周期的回波信号为

回波信号与本振信号混频滤波，幅度归一化后，略去不必要的固定相位可得中频信号为

将τk(t)带入式(3)，整理并省略极小分量项得:

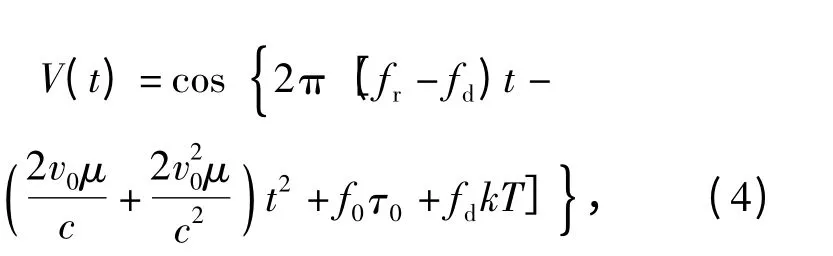
其中:fr=为静止目标的回波频率;fd=为目标的多普勒频移。由式(4)可知，不同调制周期上扫频段回波信号的中心频率均为fr-fd，出现距离速度耦合，对应的测距误差为-fdTc/4B，而相位受到fdkT 调制，不同周期k 的回波具有不同固定相位叠加，大小与目标的多普勒频率有关。同样可以证明，下扫频段回波信号的中心频率为fr+fd，对应的测距误差为fdTc/4B，相位受到-fdkT 调制。由以上分析可知，具有速度v0的目标，在上下扫频段的回波中心频率均发生偏移，出现距离速度耦合，造成测距误差，但上下扫频段对应的距离偏移大小相等，方向相反，因此对上下扫频段分别做一维FFT 变换后匹配目标，可消除距离速度耦合;而相位与目标的多普勒频率相关，相位信息反映在目标一维FFT 变换后的结果中，因此，对多个周期一维FFT 变换的结果做复数FFT 变换即可得到相位的变化率，从而求出目标的径向速度。

1.2 二维FFT 算法的局限性

测距测速精度主要由信号的均方带宽、均方时宽和信噪比决定，但在二维FFT 算法中，测距测速精度也受到FFT 变换长度、信号处理器的数据宽度的影响。主要表现在2 点:1)FFT 变换的栅栏效应，使频点存在不连续性，当目标所对应的频率落在两个频点之间时无法分辨，引入测距测速误差。2)当目标低速运行或者方位角发生变化时，目标的径向速度较小，多普勒频率较低，在一维FFT 变换后多普勒频率往往无法分辨，无法进行对消去耦合，引入测距误差。例如，在载频f0=34 GHz、B =50 MHz、T=0.2 ms、测距范围为100～300 m、信噪比为约14 dB 的系统中，假定目标初始距离为100 m，以3 m/s的速度向雷达运动，目标对应的回波频率为333.3 kHz～1 MHz，对应的多普勒频率为0.68 kHz.对于每一上扫频或者下扫频驻留时间内，进行距离维处理，对应5 MHz 的采样率，要达到0.5 m 的测距精度，距离维FFT 变换需要4 096 点;分辨3 m/s 的径向速度引起的多普勒频率，去除距离速度耦合，距离维FFT 变换需要8 192 点;达到0.1 m/s 的测速精度，速度维FFT 变换需要256 点。

由以上分析可知，在系统参数和要求确定的情况下，系统的测距测速精度与信号处理的分辨率有关。若要达到高的测距测速精度，去除较低径向速度时的距离速度耦合，则需要大的二维FFT 变换长度，而在工程处理中要兼顾实时性和成本，FFT 变换长度的增加就意味着系统的处理时间或成本的增加，这对实时信号处理系统而言是不可取的。

2 校正算法及信号处理流程

2.1 校正算法

常用的频率校正方法有:插值法，ZFFT 变换，Chirp-Z 变换，频谱质心法等多种方法，其中插值法又分为峰值搜索法，公式法等。本文选择插值公式法与二维信号处理算法相结合，主要有以下2 点考虑:1)系统的回波中频信号频率约为300 KHz～2 MHz，起始频率低，相对带宽较宽，ZFFT 变换作用不明显。2)插值公式法与Chirp-Z 变换，频谱质心法等方法相比运算量小，更能满足系统实时性需要。

插值公式法主要利用信号FFT 变换后，目标点处左右频点差值为1 的2 条谱线幅度值的比值构造一个以校正频率为变量的方程，求解出需要校正的频点值，对目标点校正补偿。设fm为信号FFT 变换后的频点，Δf 为需要校正的频点差值，信号实际频点为fm+Δf.构造如下校正比值函数

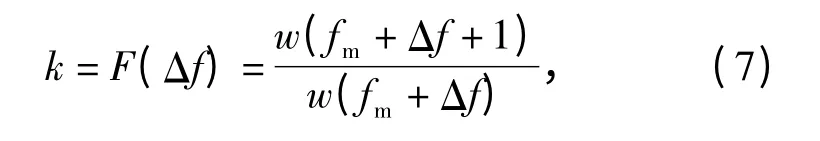
其中:w(f)为窗函数的频谱函数;k 为校正目标点处相邻谱线幅度的比值。由式(7)可知，k 是Δf 的函数，因此，对式(7)求反函数，即可算出Δf 得到实际的频点。例如a=0.5 的Hanning 窗，其频谱函数为

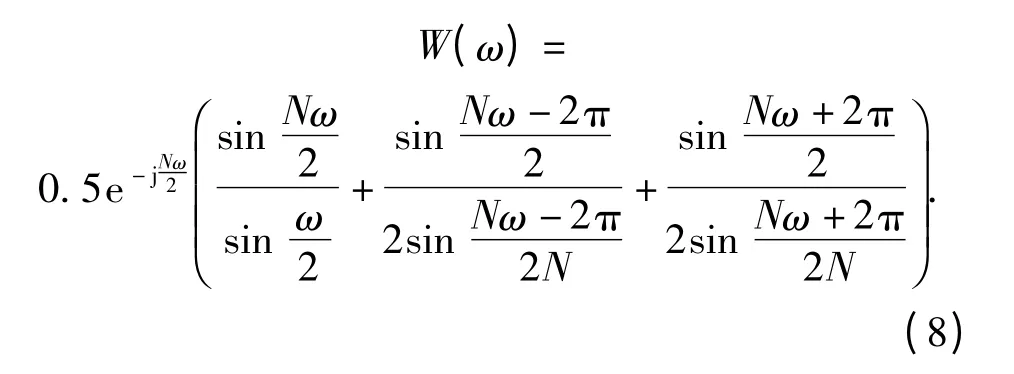
对式(8)求模，带入式(7)近似运算得:

因此，对于加Hanning 窗的数据处理，可由式(9)进行校正，同样得到矩形窗的频率校正量为经仿真计算，加窗频率校正的精度很高，相对误差在5‰以下，采用Hanning 窗和Hamming进行校正精度极高，完全可以认为无误差［4-5］。综合考虑窗函数第一旁瓣电平和衰减特性，采用Hanning 窗进行校正。

以上分析可知，校正算法可以通过有限的几次运算，对频谱进行校正，提高频域分辨率;二维FFT算法可以无模糊的测定目标的距离和速度，但是在一些特殊情况中，由于频域分辨率不够而影响系统测距测速精度;因此把两种方法结合起来，在二维FFT 变换的基础上，对频谱进行校正，不仅可以提高测距测速精度，还可以解决径向速度较小目标的去耦合问题。

2.2 信号处理流程

图1为系统的信号处理流程:首先，回波中频信号经A/D 采样后变为离散的数字信号，经过去均值，加窗，一维FFT 变换，N 周期的积累后，去除背景噪声，得到差拍信号在距离维上的频谱;经过CFAR 检测，频谱校正后对目标进行一维距离门配对和距离速度去耦合;再通过二维FFT 变换和频谱校正后求出目标速度，最后对目标进行速度维配对，得到真正目标的距离和速度。

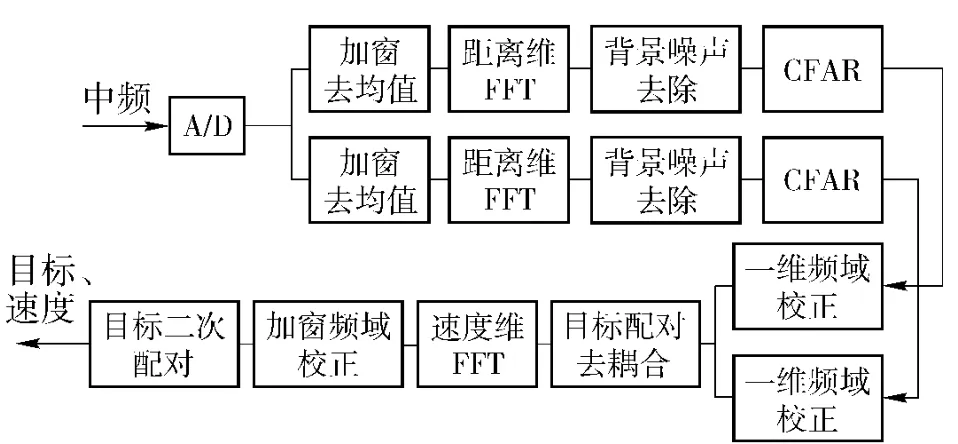
图1 系统信号处理流程Fig.1 Signal processing diagram of system

3 算法仿真及结果分析

为了验证校正算法的有效性，对它进行了仿真，仿真中设定LFMCW 雷达的具体参数如下:载频f0=34 GHz，扫频带宽B =50 MHz，三角波周期T=0.2 ms，SNR=14 dB.窗函数是a =0.5 的Hanning 窗，距离维FFT 变换点数为512 点，速度维FFT 变换为32 点。图2是静止目标校正前后的距离误差对比，目标距离范围100～300 m，步进0.5 m.由图可知:校正前，在测距范围内误差分布在［-1.5 m，1.5 m］之间，与距离维FFT 栅栏效应引入的误差相符，加窗校正后测距误差基本接近零。图3、图4为不同速度的运动目标在同一距离的校正前后对比，目标距离为200 m、径向速度范围为0～15 m/s、步进0.1 m/s，对比可知:校正前，速度约小于10 m/s 时，无法分辨多普勒频移，上下扫频段频点重合，无法配对去除距离速度耦合，速度约大于10 m/s 时，由于FFT栅栏效应，上扫频段频点和下扫频段频点与实际频点误差较大，配对后仍具有较大误差，误差的大小与目标回波所对应的频点位置有关;校正后，可以看到随着目标径向速度的增加，上下扫频段的距离出现偏差，但增大幅度相同，符号相反，因此可对目标距离速度去耦合。图5为校正前后误差对比图，校正后的距离值与目标的真实距离基本重合。

图6和图7是二维FFT 变换后速度校正前后误差对比，目标的速度误差主要由第二维FFT 变换的栅栏效应引起，按照加Hanning 窗的方法对二维FFT 变化后的结果校正。校正前，速度误差分布在［-0.3 m/s，0.3 m/s］之间，校正后速度误差明显减小，分布在［-0.1 m/s，0.1 m/s］之间。

在某实际项目中，按照图1的流程对回波中频信号进行处理，使用TI 公司DSP 芯片和Altera 公司CycloneⅡ的FPGA 芯片，32 个调频周期作为一个积累周期，每帧处理时间约为30 ms.在相同的外场测试条件下，未加校正算法的测距误差分布在［-1.5 m，1.5 m］内，测速误差分布在［-0.8 m/s，0.8 m/s］内;校正后测距误差分布在［-0.6 m，0.6 m］内，速度误差分布在［-0.2 m/s，0.2 m/s］内。校正后测距测速精度有明显的提高，满足了系统的要求。

图2 校正前后静止目标距离误差比较图Fig.2 Range error comparison of statistic target

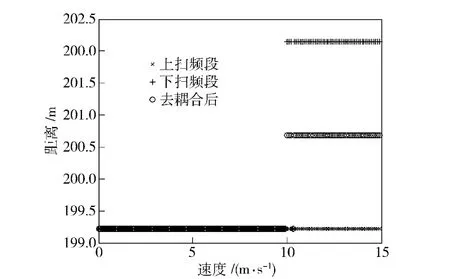
图3 校正前运动目标距离测量值Fig.3 Moving target range before calibration

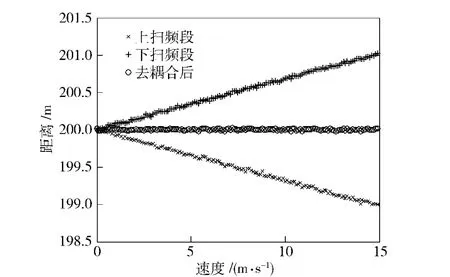
图4 校正后运动目标的距离测量值Fig.4 Moving target range after calibration

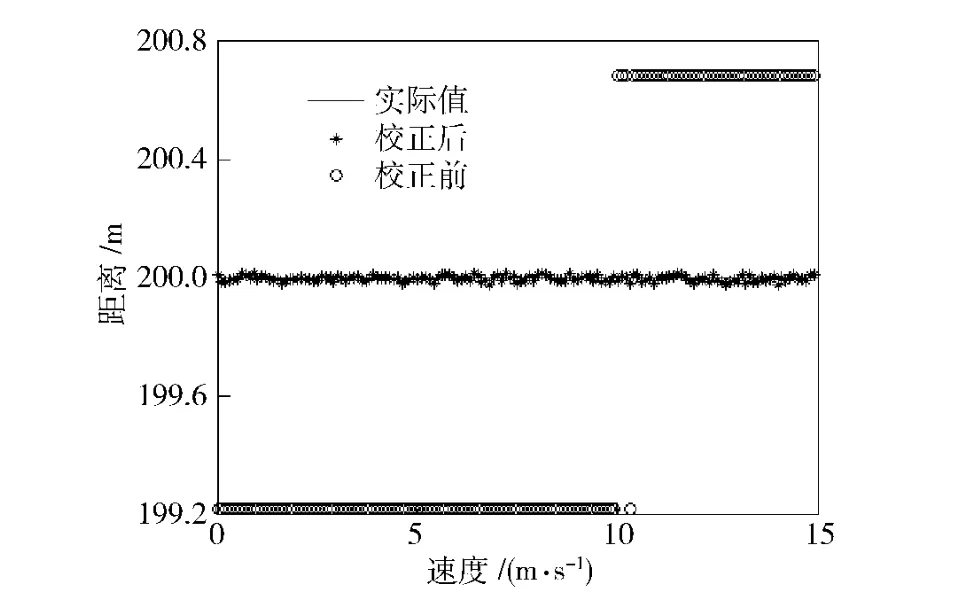
图5 校正前后运动目标距离比较图Fig.5 Range comparison of moving target

图6 校正前目标速度误差Fig.6 Velocity error before calibration

图7 校正后目标速度误差Fig.7 Velocity error after calibration

4 结束语

本文详细分析了线性调频连续波雷达的测距测速算法，针对近程防御雷达的实时性和高精度要求，将二维信号处理算法和频率校正算法相结合，对目标点处的频谱进行细化。仿真及试验表明，此方法可消除FFT 变换分辨率和栅栏效应对系统的测量精度的影响，提高雷达的测距测速精度。本方法已在实际项目中得到应用。

References)

［1］Stove A G.Linear FMCW radartechniques［J］.IEEE Proceeding-F:Radar and Signal Processing，1992，139(5):343 -340.

［2］Wojtkiewicz A，Misiurewicz J，Naiecz M，et al.Two-dimensional signal processing in FMCW radars［EB/OL］.(2007)［2009-08-01］.http:∥staff.pw.edu.pl/～jmisiure/esptr_2007/lect_fmcwfm.pdf

［3］杨建宇，凌太兵，贺峻.LFMCW 雷达运动目标检测与距离速度去耦合［J］.电子与信息学报，2004，26(2):69 -173.YANG Jian-yu，LING Tai-bing，HE Jun.MTD and range-velocity decoupling of LFMCW radar［J］.Journal of Electronics ＆ Information Technology，2004，26(2):69 -173.(in Chinese)

［4］Grandke T.Interpolation algorithms for discrete Fourier transforms of weighted signals［J］.IEEE Trans.Instrum.Meas.，1983，32(2):350 -355.

［5］丁康，谢明，杨志坚.离散频谱分析校正理论与技术［M］.北京:科学出版社，2008:101 -107.DING Kang，XIE Ming，YANG Zhi-jian.The theory and technology of discrete spectrum correction［M］.Beijing:Science Press，2008:101 -107.(in Chinese)