半捷联导引头稳定平台的双环滑模变结构控制

刘伟，柯芳，朱斌，樊键

(1.中船重工第723 研究所，江苏省 扬州市225001;2.西南技术物理研究所，四川省 成都市610041)

0 引言

近年来，随着对导引头高精度、小体积、低成本等性能的发展需要，导引头稳定平台技术的研究重心已开始转向半捷联导引头稳定技术［1］。与传统的陀螺稳定平台相比，半捷联导引头稳定平台将惯性传感器安装在弹体上而不是直接安装在稳定平台上，稳定平台框架角位置传感器信号与自动驾驶仪上的速率传感器信号相结合以测定稳定平台的惯性速率［2］。这种捷联式平台减小了导引头体积，降低了研制成本，尤其适用于空间上有限制的战术导弹应用。

然而，在导弹飞行过程中，弹体扰动不仅会引起平台本身的摩擦力矩的变化，而且还会对稳定平台框架角位置产生影响，与角位置传感器输出的角度信号产生耦合。而且，为了得到稳定平台的惯性速率，引入了自动驾驶仪上的速率传感器信号，与直接得到平台惯性速率相比，必然会引起更多的误差。此外，由于温度、气压、震动等不确定因素的影响，半捷联稳定平台系统的某些结构参数可能会产生变化，这也会给系统的稳定性带来影响。因此，半捷联平台稳定方案与陀螺平台稳定方案相比，在小体积和低成本等方面具有明显优势，但是同时给系统带来了更多地扰动和不确定因素，使系统地稳定性降低。于是如何设计出有效的控制器使系统在多种扰动和不确定性因素的环境下仍然具有很强的鲁棒性，成为半捷联导引头稳定平台研究的关键问题之一。

工程上通常采用PID 校正环节以及相位超前、滞后校正网络等线性控制器进行系统稳定。这些校正环节的设计依赖于对象的参数，即针对不同的对象参数校正环节的参数也要作相应调整。而且，线性控制器鲁棒性不够好，不能很好地克服外界扰动及参数变化对系统的不利影响［3］。

滑模变结构控制是变结构控制系统的一种控制策略。这种控制策略与常规控制的根本区别在于控制的不连续性，即一种使系统结构随时间变化的开关特性。该控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的上下运动，即所谓的“滑动模态”或“滑模”运动。这种滑动模态是可以设计的，且与系统的参数及扰动无关，这样，处于滑模运动的系统就具有很好的鲁棒性。

由于对系统的摄动可做广泛的理解和处理，除参数摄动外，非线性项和不确定项都可视为摄动，因而不失一般性地，可将对象复杂的非线性模型化为受到摄动的线性模型。这种线性系统的变结构控制算法简单，工程上易于实现，而且具有很强的鲁棒性。因此，我们用滑模变结构控制的方法来设计半捷联导引头稳定平台的伺服回路。

1 半捷联导引头稳定平台数学模型

半捷联导引头伺服稳定平台系统控制框图如图1所示。图中:K1、K2、K3分别为功放放大系数、电流环放大系数、电机力矩系数;L、R 为电枢绕组电感及电阻;J 为平台转动惯量;Kf为角位置传感器传递系数;Gc为控制器模型;Tf和υm是系统的2 个主要干扰源，分别为平台干扰力矩和弹体运动角速度。

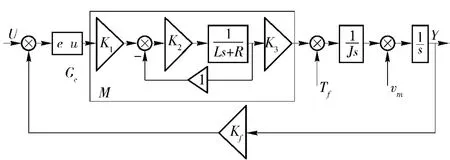
图1 半捷联稳定平台系统框图Fig.1 Half strapdown stability platform structure

图1中的矩形框内的环节M 为功放放大系数K1、电机的电流环及电机力矩系数K3的组合，其传递函数:

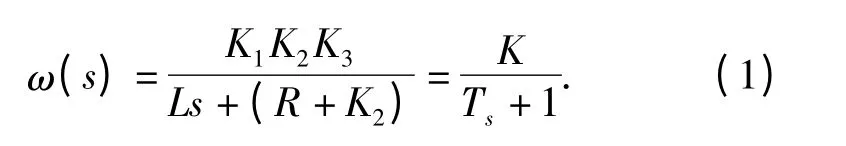
由式(1)可知，M 可以等效为一个惯性环节，其时间常数T 与电枢绕组电感L 及电阻R 和电流环放大系数K2有关。

为了使系统具有更好的稳定性和更强的鲁棒性，我们对系统进行了状态扩张［4］。另外，由于系统阶次较高，且受到多个扰动的影响，故将系统模型改进为内外环反馈控制模型，改进后的系统框图如图2所示。

图2 基于变结构控制器的系统模型框图Fig.2 System structure based on varible structure controller

N 为矩形框内所有环节构成的子系统;xd为系统伺服指令;x'd为子系统N 的输入指令;x1为平台角位置输出;x'1为平台惯性角速度;x'2为惯性环节M 的输入;Gout和Gin分别为系统的外环和内环变结构控制器。

图2中，外环为系统的位置环，平台的惯性角速度x'1与外环控制器经过积分环节后的输出进行闭环，形成速率环。由于弹体运动角速度可以通过导引头自动驾驶仪中的惯性传感器获得，而框架角位置可测，因此平台惯性角速度能够得到实时解算，内环可以实现。

系统的子系统N 在惯性环节M 的时间常数较小时，可近似为一个二阶子系统。选取合适的内环变结构控制器参数，可使N 的输出x'1以很快的速度跟随输入x'd，此时系统的外环又可以等效为一个二阶子系统。这样对于每个二阶子系统而言，只有一个干扰源，变结构控制器更容易实现，整个系统在控制上更容易实现稳定，鲁棒性会有很大提高。

首先对子系统N 进行分析，其状态空间方程为

式中，x'1、x'2为系统N 的状态变量，其物理意义同前;KM为经环节M 后的等效放大系数;Uin为待设计的内环变结构控制律。

将式(2)化为能控标准型，得

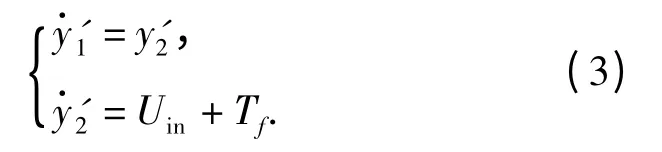
对系统N 给定输入x'd，则其输出x'1为对输入x'd的跟踪。

设内环等效放大系数为kN，建立系统外环部分等效后的状态空间方程

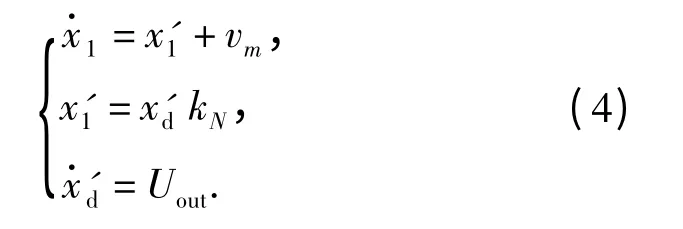
式中，x1、x'd为系统外环部分的状态变量，其物理意义同前，Uout为外环变结构控制器。

将式(4)化为能控标准型，得

式中，y1=x1、y2=x'dKN+vm.

式(3)、式(5)即为简化后的用于滑模控制器设计的导引头半捷联稳定平台系统的数学模型。滑模变结构控制器设计。

1.1 内环滑模变结构控制器

当内环子系统N 给定为x'd时，令

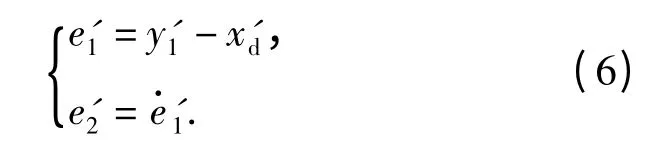
选取内环变结构控制器的切换面函数

式中，cin1为切换面参数。

由逐项优超算法［4］，设计内环控制器的控制律:

其中:αin_1、αin_2、βin1、kin为控制器的开关系数;sign为符号函数。

为了使切换面Sin=0 以外的运动点于有限的时间内到达切换面，切换函数Sin应满足:

由式(6)、式(7)、式(8)、式(9)可得:

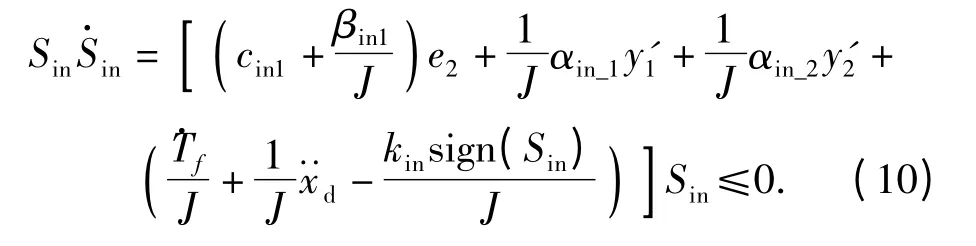
因此，内环变结构控制器的开关系数应满足:

当各开关系数满足式(11)至式(14)时，滑动模态可达。其中，开关系数kin的选取只取决于干扰力矩的一阶导数T·f和伺服指令的二阶导数x··d的大致变化范围。按照式(11)至式(14)构造变结构控制器的输出式(7)，就可保证扰动力矩Tf和对象参数对滑动模态的到达过程没有影响，切换面参数cin1对滑动模态本身的性能起决定性作用，是设计者选定的参数，与系统扰动和参数的变化无关。这样，构成系统动态行为的两个阶段，即趋近滑动模态的过程和滑动模态过程本身均对Tf和参数变化具有自适应性，则由变结构控制器所闭环的半捷联稳定平台内环子系统对外界扰动和参数变化具有强鲁棒性。

1.2 外环滑模变结构控制器

按照同样的方法我们来设计外环滑模变结构控制器。对给定的伺服指令xd，令:

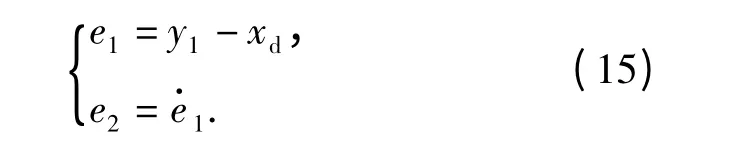
选取外环变结构控制器的切换面函数

其中，cout1为外环滑模面参数。

设计外内环控制器的控制律:

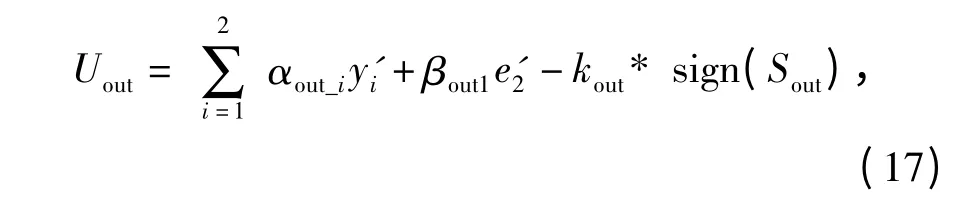
其中，αout_1、αout_2、βout1、kout为外环控制器的开关系数。

由滑动模态动态可达条件

可得:当

时，滑动模态可达。

由式(19)至式(22)可见，开关系数kout的选取取决于弹体的角加速度和伺服指令的二阶导数的大致变化范围。按照式(19)至式(22)构造外环变结构控制器，就可保证弹体扰动和对象参数对外环滑动模态的到达过程没有影响，切换面参数cout1的选定与系统扰动和参数的变化无关。因此和内环子系统一样，外环部分的趋近滑动模态的过程和滑动模态过程本身均对扰动和对象参数变化具有自适应性。

2 仿真分析

根据式(8)和式(17)，构造导引头半捷联稳定平台的外环变结构控制器Gout和内环变结构控制器Gin，在matlab 环境下建立如图2所示的半捷联平台伺服系统控制模型，系统参数略。

在图2中，内外环变结构控制器的输出经过积分环节后加入系统的输入端，一方面对系统进行状态扩张，另一方面，有效减小了变结构控制器自身抖动对系统的影响，从而提高了系统的稳定性。

在相同的仿真环境下建立基于PID 控制器的导引头半捷联稳定平台，通过两种控制方法的性能比较，验证变结构控制的鲁棒性和对系统参数变化的适应性。

图3和图4分别为2 系统模型的单位阶跃响应和系统的电机控制力矩，其仿真条件为:输入信号为单位阶跃信号;弹体运动为幅值2°、频率1 Hz 正弦运动;干扰力矩为方差0.01 的随机信号。

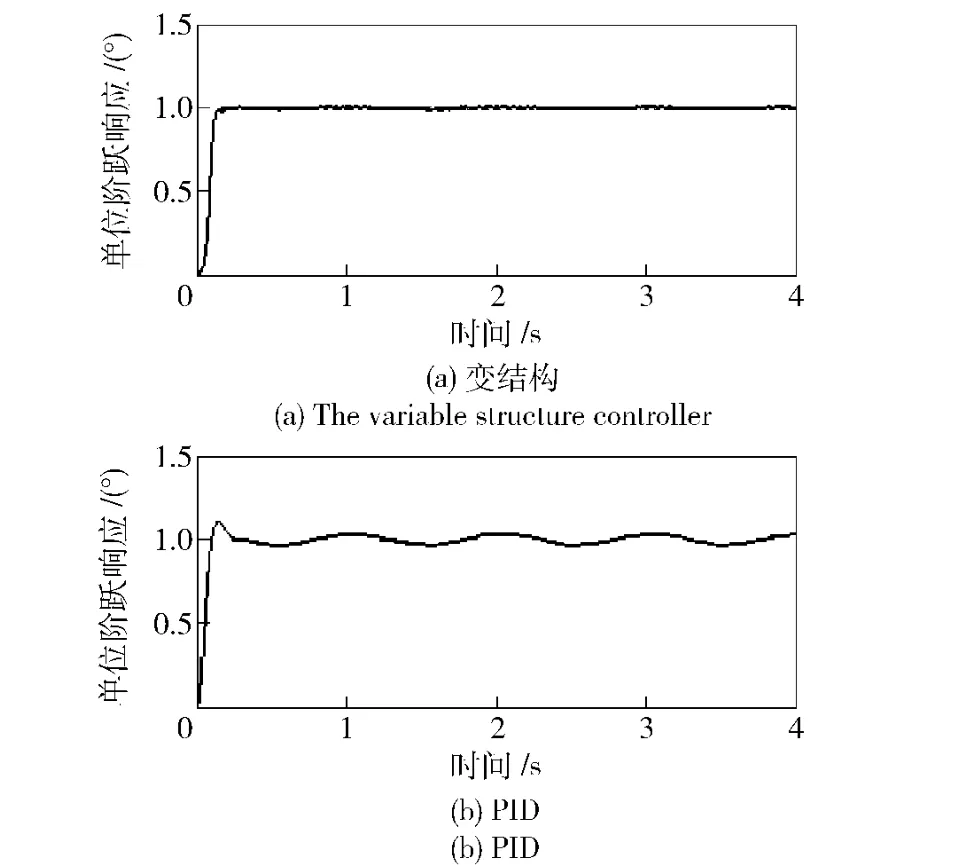
图3 单位阶跃响应Fig.3 Step responses comparison

图4 电机控制力矩Fig.4 Control moments comparison of motors

由图3可见:变结构控制的输出响应具有很好的快速性，且没有超调，系统进入稳态后并没有产生明显的抖动，克服了控制器本身的影响，系统对干扰力矩和弹体扰动具有很强的鲁棒性;而基于PID 控制器的系统模型输出有一定超调，且系统进入稳态后明显受到了弹体扰动和干扰力矩的影响。

通过图4中两系统的电机力矩输出曲线可见:变结构控制相对于PID 控制对系统对象的控制量更小，这有利于降低对象参数性能指标的要求。

图5为2 系统模型隔离度仿真的系统输出响应。其仿真条件为:输入信号为0;弹体运动为幅值4°、频率2 Hz 的正弦运动;干扰力矩为方差0.01 的随机信号，以上为条件1。将平台的转动惯量变为原来的2 倍，其余参数不变，此为条件2，转动惯量变化后2 系统的输出响应曲线如图6所示。

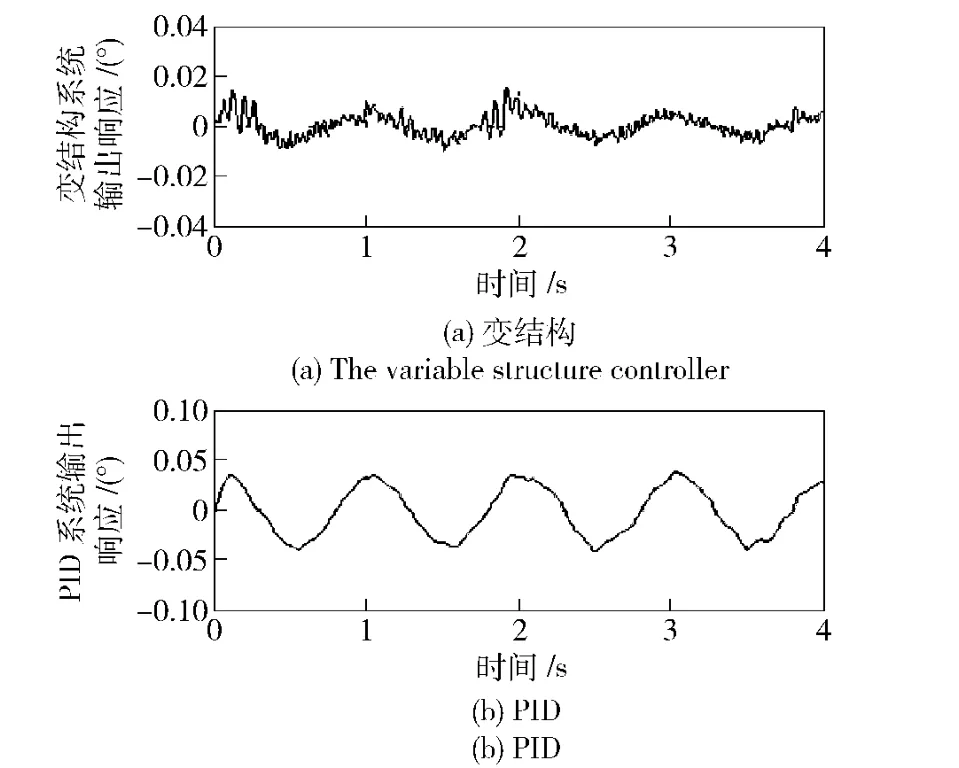
图5 两个系统在条件1 下的输出响应Fig.5 System output response in condition 1

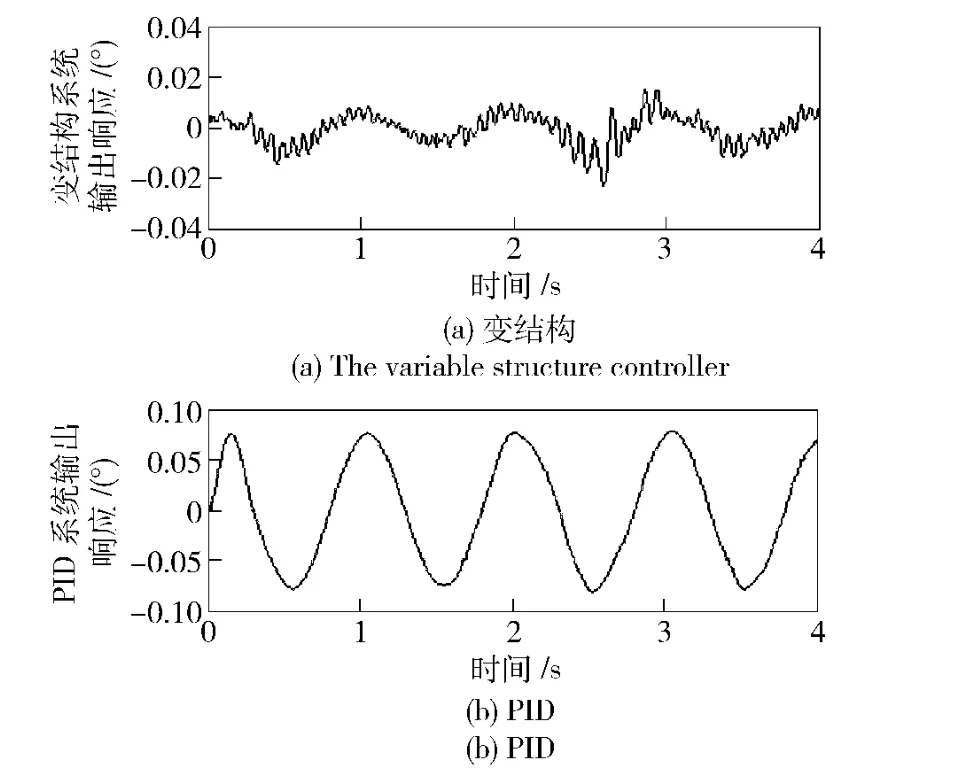
图6 两个系统在条件2 下的输出响应Fig.6 System output response in condition 2

由于扰动大小随时间变化而变化，因此，为了能够准确反映系统对外界扰动的隔离性能，引入角位置精度作为衡量指标，即系统输出角度响应曲线的均方差。图5中基于变结构控制器和基于PID 控制器的系统模型平台角位置精度分别为0.077 mrad和0.599 mrad，而系统参数变化后，角位置精度分别变化为:0.108 mrad 和1.299 mrad，如图6所示。结果表明，当系统结构参数发生变化时，基于变结构控制器的系统输出比基于PID 控制器的系统输出具有更强的鲁棒性。

3 结论

以上的理论分析及仿真结果表明，在导引头半捷联稳定平台伺服回路中采用位置环和速率环的双环变结构控制相对线性控制具有明显的优势，能较好地完成对伺服指令的跟踪，并能有效地克服干扰力矩和弹体扰动对平台的影响，具有较好的隔离度。滑模变结构控制算法简单、易实现，在有精确角位置传感器硬件保障和优良的微分算法条件下可望在半捷联导引头稳定平台伺服回路中获得应用。

References)

［1］华宇清，于国宏.捷联系统姿态算法比较及研究［J］.航天控制，1995(3):10 -16.HUA Yu-qing，YU Zhi-hong.Comparability and research of stance algorithm on strapdown system ［J］.Aerospace Control，1995(3):10 -16.(in Chinese)

［2］张聘义，祁载康.一种匹配滤波方法在导引头捷联稳定平台中的应用研究［J］.红外技术，2005(1):6 -10.ZHANG Ping-yi，QI Zai-kang.The application of matching filter in the strapdown seeker platform research［J］.Infrared Technology，2005(1):6 -10.(in Chinese)

［3］柯芳，樊键，尹小杰.陀螺稳定平台伺服系统变结构控制［J］.弹箭与制导学报，2009，(6):67 -69.KE Fang，FAN Jian，YING Xiao-jie.Variable structure control on servo loop of gyro stabilized platform［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2009(6):67-69.(in Chinese)

［4］高为炳.变结构控制理论［M］.北京:中国科学技术出版社，1990.GAO Wei-bing.Variable structure control theroy［M］.Beijing:Science Press，1990.(in Chinese)