基于最优阈值法的曲轴缺齿位置判定研究

刘兴华，王裕鹏，刘福水，梁海强

(北京理工大学发动机实验室，北京100081)

0 引言

能够准确而快速地计算发动机的上止点位置和转速是发动机实现稳定运行的前提条件。电控发动机是通过在曲轴上加装正时齿盘的方式来计算曲轴位置，不同的发动机有着不同的正时齿轮，它是通过总齿数和缺齿数来命名，例如，60-2(均布60 齿去掉2 齿)、36-2 等正时齿轮方案。虽然不同类型的正时齿轮具有不同的总齿数、缺齿数，但是它们却实现着相同的功能［1］。通过从正时齿盘上两个齿信号之间的时间差可以算出当前转速，从缺齿位置开始对信号计数可得当前曲轴位置。因此准确判定缺齿位置对电控系统乃至整个发动机的稳定运行有着十分重要的意义。

文献［2 -3］中分析了噪声对瞬态曲轴转速信号的影响，讨论了曲轴转速信号消噪方法，通过采用插值、双传感器方法准确地定位了发动机活塞的运行位置，有效地消除噪声对转速信号的影响。文献［4］中研究了识别曲轴缺齿位置的方法，文中原理上探讨了判断当前齿为缺齿或正常齿的方法，但没有考虑不同阈值的选取对缺齿位置准确判定带来的影响。文献［1］中介绍了常见的正时齿盘形式，建立了适用于任意凸轮轴和曲轴正时齿盘形式的发动机曲轴位置追踪算法，该算法对为发动机处于稳态和瞬态工况时提供了精确和迅速的发动机曲轴位置信息，为发动机的控制建立了基础。文中的曲轴位置追踪算法中建立了不同正时齿轮形式表，通过查表的方式来获取缺齿的位置。

本文在前人研究的基础之上，采用最优阈值统计算法从理论上求出了确定当前齿是否为缺齿的最优阈值Tjudge的通用公式。首先，在电控氢气发动机上采集了瞬时转速试验数据;其次，对试验结果进行了分析，求出了不同转速下正常齿的方差分布，并认定当前转速与上个转速的瞬时转速比ncurrent/nlast的概率分布服从正态分布;然后，通过分析缺齿判定条件，建立了信号齿盘概率分布的数学模型，并根据最优阈值统计算法来进行缺齿位置的判定;最后，代入计算的方差求出了判断当前齿是否为缺齿的最优阈值Tjudge的通用公式，求出了缺齿出现误判时转速波动率的临界值，并通过3 种正时齿盘方案验证了该公式的正确性。

1 试验研究

1.1 试验装置

试验条件及试验系统简图见表1和图1.

1.2 试验过程

发动机开始运行后，固定减压阀后的氢气压力0.3 MPa，固定点火提前角在上止点前5°CA，固定喷氢提前角在330°CA，喷氢持续期为40°CA，维持冷却水温75 ℃.改变发动机转速，用燃烧分析仪分别记录550、650、1 000、1 500、2 000、3 000、3 500、4 000、5 000 r/min 下的瞬时转速数据。燃烧分析仪每隔0.5°CA 采集一个瞬时转速，实时记录各循环内瞬时转速的变化过程。

图1 氢气发动机系统简图Fig.1 Schematic diagram of H2ICE

表1 氢气发动机参数Tab.1 Parameter of H2ICE

1.3 试验结果分析

对采集的氢气发动机处于不同瞬时转速时的实验数据进行分析，画出了瞬时转速比ncurrent/nlast概率分布的直方图。直方图结果表明，所研究的转速下，瞬时转速比ncurrent/nlast的概率直方图均为中间高、两边低均值为1 的钟形正态分布曲线。以转速为650 r/min 为例，如图2所示，其瞬时转速比ncurrent/nlast概率分布的直方图服从均值为1，方差为0.000 250 424 的正态分布。

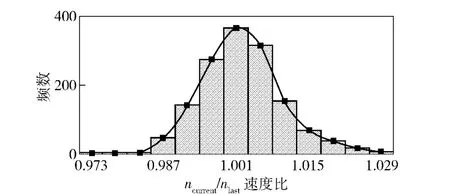
图2 瞬时转速比ncurrent/nlast概率分布直方图Fig.2 Probability distribution column diagram of the speed ratio

对不同转速的试验数据进行分析，得到正常齿的方差，为后续理论计算提供参考。不同转速下方差的分布见图3.

图3 不同转速下正常齿方差分布图Fig.3 The variance distribution of the teeth under different speed

2 数学建模及分析

2.1 缺齿判定条件

图4为采集的曲轴信号，其中虚线的部分为2个缺齿。曲轴运行到正常齿时，当前齿计算的瞬时转速ncurrent与上一个齿计算的瞬时转速nlast之比应该约等于1;而当曲轴运行到缺齿处时，瞬时转速比ncurrent/nlast应该约等于1/(n +1)(n 为缺齿数)。根据此原理，通常满足下面条件时，单片机就认定当前齿为缺齿的位置:

式中，Tjudge为本文中要求解的最优阈值，也就是利用此值来判定曲轴缺齿的位置。当瞬时转速比ncurrent/nlast小于Tjudge时，则判定当前齿为缺齿;若瞬时转速比ncurrent/nlast大于Tjudge时，则判定当前齿为正常齿。当正确判断出缺齿位置，就可根据上止点和缺齿之间的固定的间距来实时表征当前曲轴所处的位置。但需注意的是，因为瞬时转速比服从正态分布，因此无论阈值如何，理论上都存在误判的概率，本文旨在寻找误判概率最小的最优阈值。

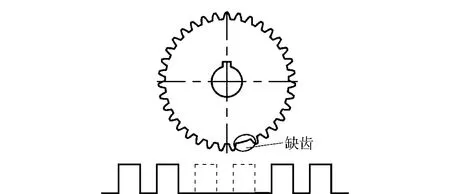
图4 正时齿盘及采集到的曲轴信号Fig.4 Crank-shaft tooth wheel and its signal

2.2 数学建模

经过上面的论述可知，出现正常齿X 的概率密度分布和出现缺齿Y 的概率密度分布都为正态分布，正常齿期望φ1=1，设其方差为δ1;那么缺齿的期望值φ2=1/(n+1)，设其方差为δ2.则正常齿X的概率密度函数为

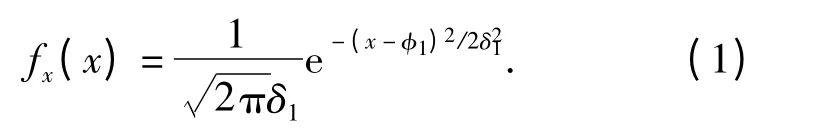
缺齿的函数g(x)为

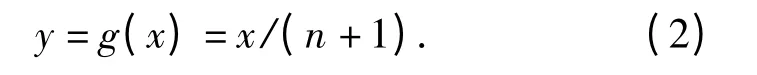
正常齿的函数h(y)为

其中，h(y)是反函数g(x).

因此，Y=X/n 的概率密度为

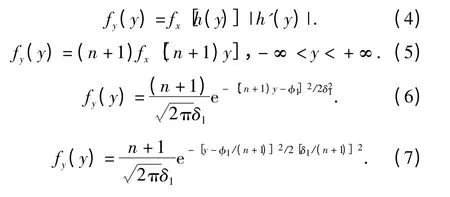
由上面的推导可知，正常齿的方差是缺齿方差的n+1 倍，即:δ1=(n+1)δ2.

2.3 最优阈值法求Tjudge及缺齿误判率

最优阈值方法是图像分割技术中的一种统计算法［5］。该方法的思想是要找到一个最优阈值Tjudge使研究对象被错误划分的概率最小，如图5所示。本研究中的错误划分有2 类，一类是将缺齿误划为正常齿;另一类是将正常齿错误的划为缺齿。该方法把每个计算的瞬时转速比ncurrent/nlast与最优阈值Tjudge进行比较，根据它是否超过该阈值Tjudge将其划分为缺齿或者正常齿，关键的部分是最优阈值Tjudge的确定。

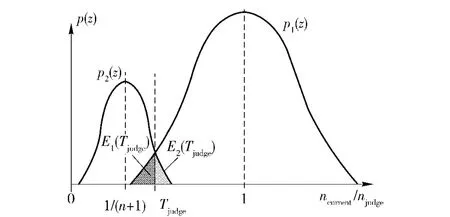
图5 最优阈值Tjudge确定的示意图Fig.5 Schematic diagram to determine optimal threshold Tjudge

设正常齿概率密度函数为p1(z)，缺齿概率密度函数为p2(z)，数齿正确概率密度函数为p(z)，则:

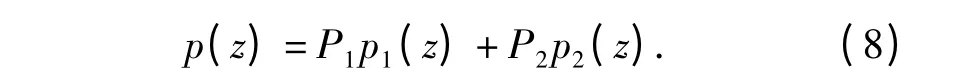
P1=(Tteeth-n-1)/(Tteeth-n)，P2=1/(Tteeth-n)，P1和P2为先验概率，P1+P2=1，Tteeth为信号齿盘的总齿数。

设正常齿的分布函数为Y =f(x)，则缺齿的分布函数为

由于Y 为n +1 倍的P2，因此设定P'2来代替P2，方便后续计算:

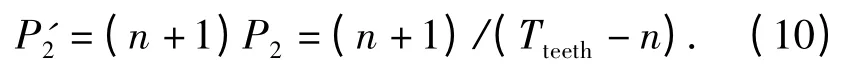
由上图4可知，正常齿判错的概率为

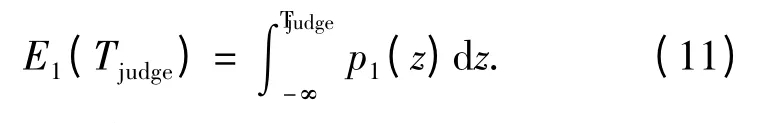
而缺齿判错的概率为

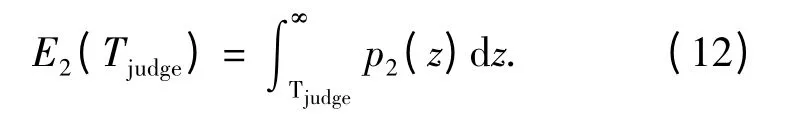
数齿错误的总错误概率为

确定最优阈值Tjudge，就要使误差E(Tjudge)最小。把E(Tjudge)对Tjudge求导，得到:

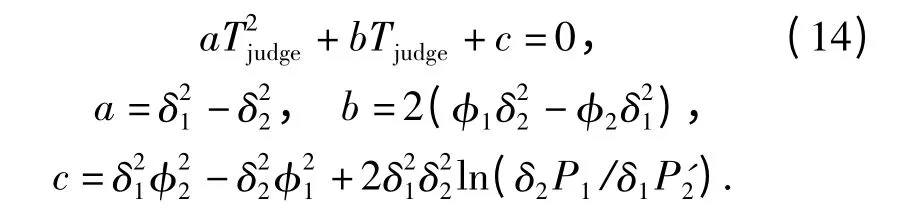
把正常齿期望φ1=1，方差δ1=(n +1)δ2;缺齿的期望值φ2=1/(n+1)，方差δ2代入上式，即得:

把上述的a、b、c 带入式(14)中求解Tjudge可得:

由图3分析可知，δ1在550 r/min 时，方差最大为0.000 655 45，代入上式中可得

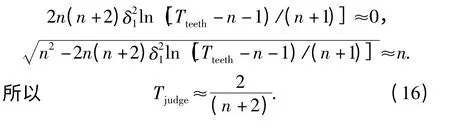
由此也可得到当缺齿出现误判时，转速波动所对应波动率的临界值ΔT 为

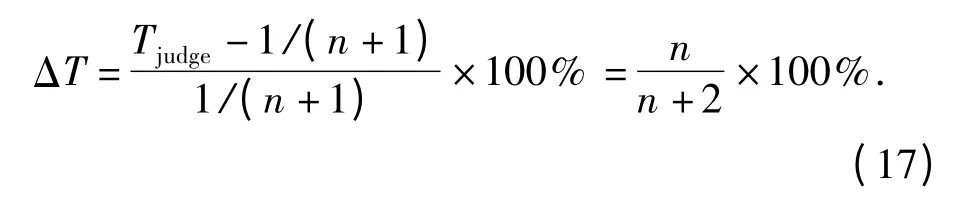
转速波动率T 可以由下面公式求出

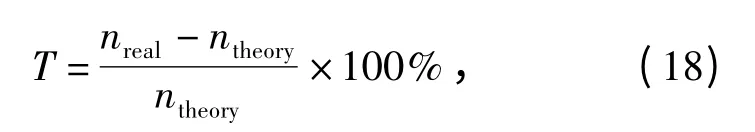
其中nreal为当前齿计算的实际转速，而ntheory为转速不波动时当前齿计算的理论转速。缺齿数与转速波动率临界值ΔT 之间关系见图6.

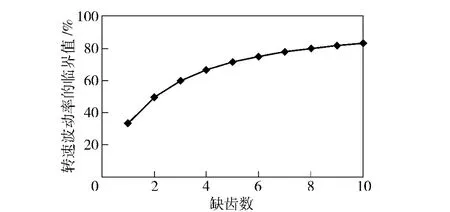
图6 缺齿数与转速波动率临界值间关系图Fig.6 The relationship between missing teeth numbers and the threshold value of speed fluctuation rate

以2 个缺齿为例，当转速波动率T 超过临界值ΔT 的50%之后，就会出现缺齿误判现象。而2 个齿之间计算转速的时间非常短，是ms 级别的数值，内燃机转速虽然是动态的过程，但其变化也是一个过程，这么短的时间转速波动率是非常小的，因此实际内燃机工作过程中出现缺齿误判的几率很小。

同时从图6可以看出，随着缺齿数的增加，允许转速波动率的临界值在不断提高，因此增加缺齿数对防止缺齿位置误判是十分有利的。

3 实验验证

通过上述结论可以看出，缺齿判定条件瞬时转速比ncurrent/nlast＜Tjudge中，Tjudge的最优解为

Tjudge为缺齿数.

下面采用2 套正时齿盘方案来验证上述推导的结论，一个正时齿盘为60-3 方案，另一个为30-2 方案。氢发动机用上述2 种正时齿盘发出的曲轴定位信号作为输入信号，其转速控制为2 000 r/min.同时，通过上位机实时记录下单片机内计算的相邻2个齿之间的转速，实验结果见图7.

在图7中正时齿盘为60-3 方案，ECU 内最优阈值Tjudge选定为2/5，此时氢发动机及ECU 能够正常稳定的运转。从单片机内计算的瞬时转速可以看出，在氢发动机运转一个循环内共记录下114 个瞬时转速，在缺齿位置时的瞬时转速为正常齿处瞬时转速的1/4，验证了缺齿数为3 时最优阈值Tjudge取为2/5 是合理的。

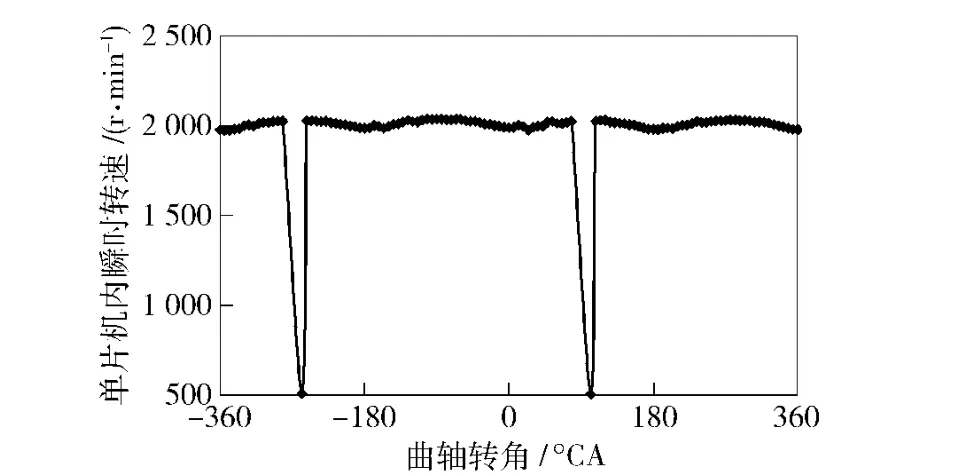
图7 齿盘60-3 时单片机内瞬时转速Fig.7 Instantaneous speed in MCU on the 60-3 timing wheel

在图8中正时齿盘为30-2 方案下，ECU 内的最优阈值Tjudge选定为1/2，此时氢发动机同样能够正常稳定的运转。在氢发动机运转一个循环内单片机共记录下56 个瞬时转速，缺齿位置处的瞬时转速为正常齿处瞬时转速的1/3，验证了总齿数为30 时最优阈值取值为1/2 是合理的。同时，加上之前试验中采用的正时齿盘为60-2 时最优阈值亦为1/2，也说明了总齿数对最优阈值Tjudge的取值范围没有影响，它只与齿盘上的缺齿数有关。

图8 齿盘30-2 时单片机内瞬时转速Fig.8 Instantaneous speed in MCU on the 30-2 timing wheel

4 结论

1)在所研究转速范围内，当前转速与上个转速的瞬时转速比ncurrent/nlast的概率分布服从均值为1的正态分布。随着转速的升高，瞬时转速方差呈先急后缓的下降趋势。

2)通过60-2、60-3 和30-2 三种正时齿盘方案，验证了本文提出的不同正时齿盘所对应的最优阈值的通用公式是正确的。从理论上分析可知，它适用于所有电控发动机用来判定缺齿位置，进而判缸。

3)从最优阈值的通用公式和实验结果分析可知，无论正时齿盘的总齿数Tteeth为多少，最优阈值均与其无关，只与齿盘上的缺齿数有关。

4)利用最优阈值分析了缺齿出现误判时转速波动率的临界值，转速波动率不得超过该值。同时，增加缺齿数对防止缺齿位置误判是十分有利的。

References)

［1］Wang J，Sarlashkar J.Engine crankshaft position tracking algorithms applicable for given arbitrary cam-and crank-shaft position signal patterns［R］.SAE:2007，1:1597.

［2］Patrick Leteinturier，Joseph Benning.Enhanced engine position acquisition ＆ treatment［R］.SAE:1999 -01 -0203.

［3］LI Jian-qiu，YANG Ming-gao.Momentary engine speed signal measurement:noise analysis and compensation［R］.SAE:2000-01 -0544.

［4］甄龙信，安子君，李强，等.基于曲轴位置传感器信号的曲轴角加速度分析［C］∥2008 中国汽车工程学会年会论文集.天津，2008:95 -99.ZHEN Long-xin，AN Zi-jun，LI Qiang，et al.Crank angular acceleration analyzing based on crank position sensor signal［C］∥The collection of 2008 SAE-China thesis.Tianjin，2008:95 -99.(in Chinese)

［5］章毓晋.图象分割［M］.北京:科学出版社，2001:70 -76.ZHANG Yu-jin.Image segmentation［M］.Beijing:Science Press，2001:70 -76.(in Chinese)