基于分数阶傅里叶变换的标量脱靶量测量新方法
邓兵,陶然,董云龙
(1.海军航空工程学院 电子信息工程系,山东 烟台264001;2.北京理工大学 信息与电子学院,北京100081)
0 引言
基于无线电技术的靶标坐标系标量脱靶量测量方法主要有窄脉冲测量法和多普勒测量法[1,2]。多普勒测量方法的基本原理是依据弹靶交会过程中回波信号多普勒频率随时间变化的规律由导弹与靶标的相对运动速度、相对运动加速度、标量脱靶量、脱靶时刻来决定。也就是说,如果能够测出交会过程中导弹回波多普勒频率随时间的实际变化曲线,然后基于选定的多普勒频率曲线模型采用最优化方法进行最优拟合,就能估计出被测导弹相对于靶标的标量相对运动速度、脱靶距离等标量脱靶量参数。
当前使用的测频方法都是建立在恒幅恒频的假设前提下,然后采用基于FFT 的谱分析或超分辨的现代谱分析等方法来进行频率测量[2-5]。其基本做法是对接收信号作分段处理,假定其在每小段内近似为恒频恒包络的谐波信号,然后对每小段信号作限带降噪来抑制噪声,并对降噪后的信号估计出瞬时频率。
由于常规的谱分析算法受到瑞利限的限制,因此希望分段的长度比较长,以提高频域分辨率。而脱靶量测量中由于多普勒频率的快速变化而对回波信号的分段通常较短。这就造成了利用恒幅恒频的假设来估计信号频率在脱靶点附近,尤其是在小脱靶量的情况下,会引起较大的测频误差。
本文利用分数阶傅里叶变换这一有效工具,提出了一种基于恒幅chirp 信号假设的准实时标量脱靶量测量方法。该方法兼顾了运算量和测量精度的折中,在较低信噪比的条件下仍具有较好的性能。
1 测量模型
本文所研究的标量脱靶量测量系统的靶标坐标系如图1所示。靶标(测量天线)位于坐标原点,交会过程中,导弹作匀速直线运动,该系统的测量任务就是测量导弹的如下运动参数:v 是标量相对运动速度,L0是起始时刻t0的导弹位置到脱靶点的距离,r0是标量脱靶量。
在匀速直线运动模型下,导弹反射回波所产生的多普勒频率为


图1 导弹相对测量天线的运动模型Fig.1 The movement model about the missile and the measuring antenna
则多普勒周期数

通过整理后可得

在离散时间的情况下,可以用求和代替积分,即

式中:采样时刻tm,m=1,…,M,Ts为采样周期。将各时刻的结果代入式(3),便能建立如下方程组
本研究采用探索性因子分析方法来验证结构效度。首先需要对数据进行KMO样本测量和Bartlett球体检测来判断问卷是否适合做因子分析。一般KMO值在0.8以上,Bartlett球形检验的显著水平(Sig.)<0.05表明可以做因子分析,本研究问卷的KMO 测量值>0.8,同时Bartlett球体检测的显著性概率<0.05,因此适合做因子分析。KMO和Bartlett的检验结果见表3。
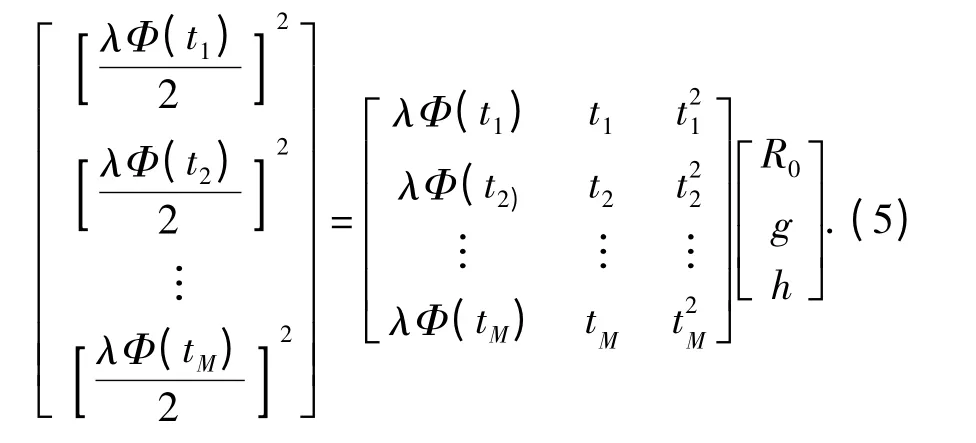
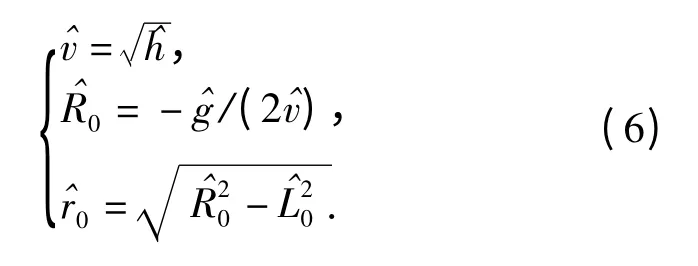
2 原理及算法
根据上述测量模型,可以知道多普勒频率的测量是其中的关键环节。
由图2可以看出,多普勒频率变化曲线大致可以分为3 部分。前后两部分近似于水平直线,中间一部分在脱靶点附近,多普勒频率变化很大,可近似为一条斜线。3 部分曲线连接处斜率变化较大,但段内曲线稳定性较好,因此,如果能知道各小段曲线的斜率(调频率μ)和频移量(中心频率fc),就可以利用各小段斜线有效地拟合出多普勒频率变化曲线。
综上所述,解决分段时长与测频精度之间的矛盾,且不带来过重的运算负担的可行措施之一就是:合理地延长分段时长,然后将每小段内信号按照恒幅chirp 信号的假设来处理。在该假设前提下,文献[2]研究了基于离散多项式相位变换(DPT)和约束解线调技术(CDT)的脱靶量测量方法,均得到了较好的测量精度。不过,DPT 法由于算法的混合项问题而对噪声较为敏感,而CDT 法是通过增加解线调环节来满足恒幅恒频假设,以回避对chirp 信号的直接处理,这样的方式必将增加运算量[2]。
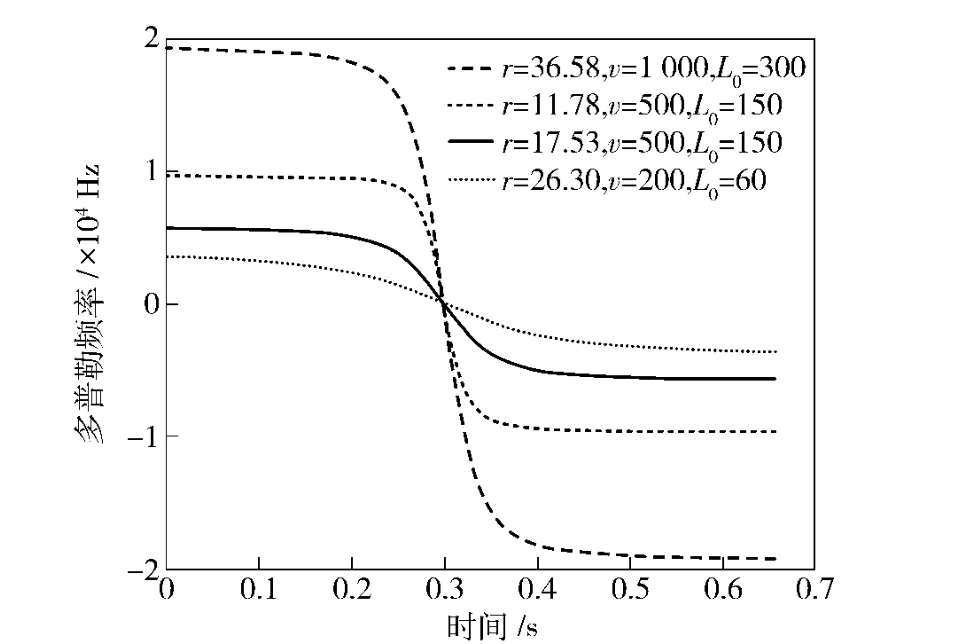
图2 不同运动参数下多普勒频率随时间的变化Fig.2 The change of Doppler frequency versus the time with the different movement parameters
分数阶傅里叶变换作为传统傅里叶变换的广义形式,近年来其相关理论得到了迅速的发展[6]。由于其实质是一种统一的时频变换,与常用二次型时频分布不同的是它不受交叉项困扰,且可以理解为chirp 基分解,因此,它十分适于处理多分量chirp 信号[7]。此外,分数阶傅里叶变换具有比较成熟的快速离散算法(与FFT 计算量相当)[8-9]。因此,本文以分数阶傅里叶变换为处理工具,以期提供一种满足一定精度要求、计算复杂度较低同时对噪声不太敏感的脱靶量测量方法。
结合第1 节的测量模型,得到具体的算法步骤如下:
1)对回波信号作预滤波处理,以提高信噪比。
2)在确定信号分段时长a 与步进拟合时长b后,从起始时刻t0开始对时长为a 的第1 个分段[t0,t0+a]的信号按照恒幅chirp 信号的假设来估计调频率μ1和中心频率fc1(具体算法和注意事项可参看文献[7,10 -11]),并根据估计值拟合出时长为b 的时段[t0,t0+b)的多普勒频率变化曲线;然后接着进行从t0+b 时刻开始的时长为a 的第2 个分段[t0+b,t0+b+a]信号的参数估计,即μ2和fc2,并依据μ2和fc2的估计值完成第2 个时段[t0+b,t0+2b)的多普勒频率变化曲线的拟合。依次递推下去,第n 个分段[t0+(n-1)b,t0+(n -1)b +a]信号完成μn和fcn的参数估计,以及第n 个时段[t0+(n-1)b,t0+nb)的多普勒频率变化曲线的拟合,直到多普勒频率的拟合长度足以进行下一步的标量脱靶量估计(一般需要拟合的多普勒频率长度超过脱靶点时刻)。注意:为了保证各分段信号的调频率和中心频率估计精度,以及提高对弱信号的估计能力(即:提高脱靶量估计的灵敏度),要求分段时长在满足恒幅chirp 信号的假设前提下尽可能的大;同时,为了保证多普勒频率变化曲线的拟合精度,又希望拟合步长足够精细,因此,本文采用分别确定分段时长a 与步进拟合时长b 的方式,并使得a >b.
3)根据第1 节所述的测量模型对第2 步所得到的多普勒频率变化曲线作非线性优化拟合,便可以估计出相应的标量脱靶量参数和
3 计算结果与比较
3.1 性能仿真
在10 dB 和0 dB 的信噪比下,分别对4 组不同运动参数的目标做标量脱靶量估计,每组运动参数分别作200 次Monte-Carlo 仿真,仿真参数如下:采样频率为78 125 Hz;波长为3/29 m;以帧为时间单位,一帧数据包含512 个数据样本,即约等于6.553 6 ms;分段时长a =2 帧,步进拟合时长b =1 帧,总的拟合时长为70 帧。所得脱靶量估计的均方根误差(RMSE)列于表1和表2.从仿真结果可以看出本文算法具有较好的估计精度。
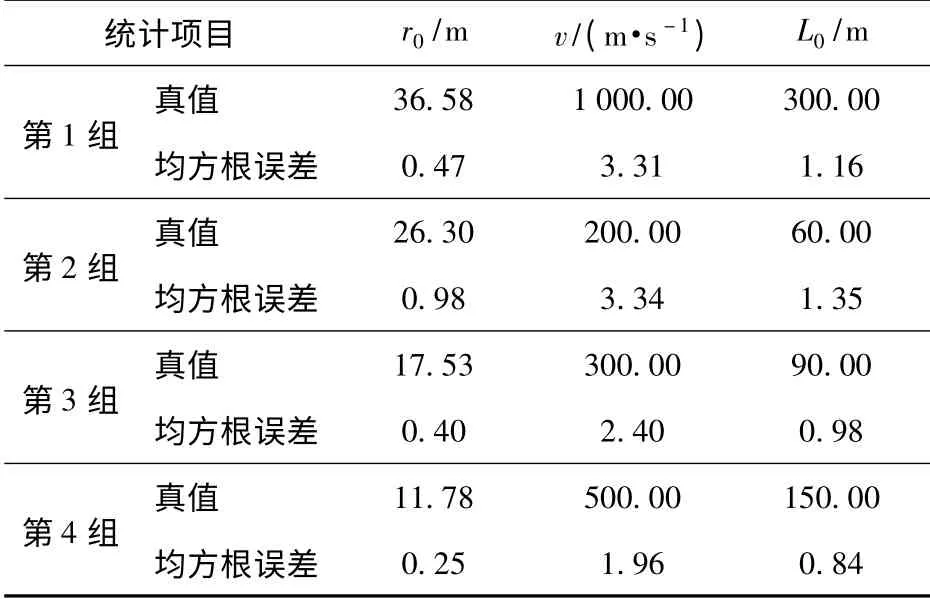
表1 10 dB 下的标量脱靶量估计误差Tab.1 The measurement error of scalar miss distance with the SNR equaling 10 dB

表2 0 dB 下的标量脱靶量估计误差Tab.2 The measurement error of scalar miss distance with the SNR equaling 0 dB
3.2 比较
接下来,我们对比分析了本文算法和基于FFT的脱靶量估计算法[4],分别简写为FRFT-MDM 和FFT-MDM.其仿真结果如图3~图5所示,结合图2,可以看出:

图3 r0 =26.30 m,v=200.00 m/s,L0 =60.00 m 时,2 种算法对脱靶量r0的估计均方根误差图Fig.3 The measurement RMSE of miss distance r0 using the two algorithms respectively when r0 =26.30 m,v=200.00 m/s,L0 =60.00 m

图4 r0 =11.78 m,v=500.00 m/s,L0 =150.00 m 时,2 种算法对脱靶量r0的估计均方根误差图Fig.4 The measurement RMSE of miss distance r0 using the two algorithms respectively when r0 =11.78 m,v=500.00 m/s,L0 =150.00 m
1)在较低信噪比情况下,FRFT-MDM 算法要明显优于FFT-MDM 算法;
2)如图3所示,多普勒频率变化较为缓慢时,两种方法均表现出较强的鲁棒性,即,随着信噪比的下降,脱靶量估计精度并没有明显的下降;
3)如图5所示,多普勒频率变化较为剧烈的情况下,FRFT-MDM 方法仍具有较好的鲁棒性,而FFT-MDM 方法则随着信噪比的下降而误差明显增大。
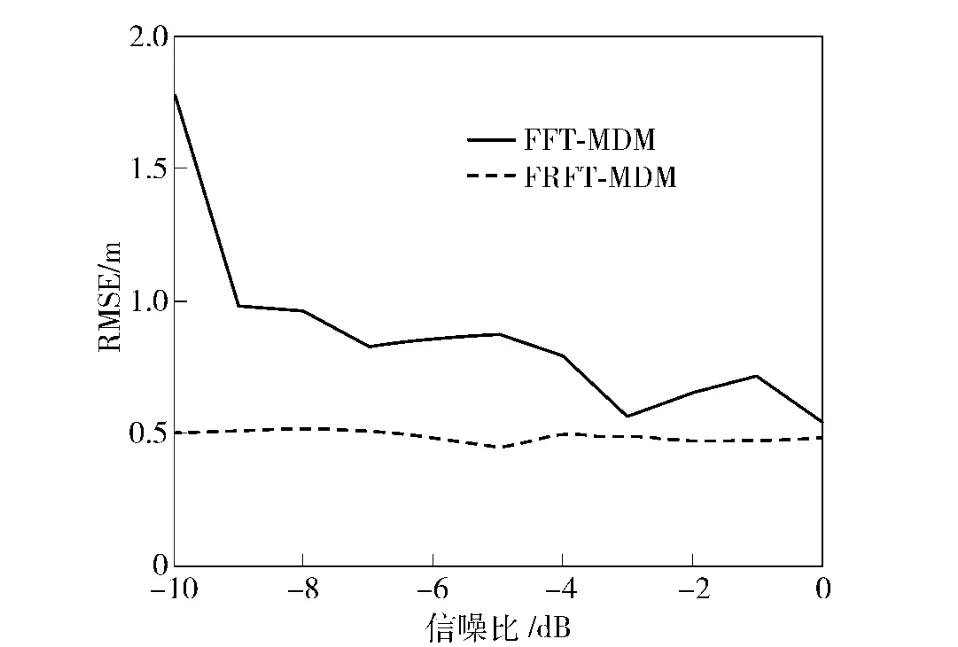
图5 r0 =36.58 m,v=1 000.00 m/s,L0 =300.00 m 时,2 种算法对脱靶量r0的估计均方根误差图Fig.5 The measurement RMSE of miss distance r0 using the two algorithms respectively when r0 =36.58 m,v=1 000.00 m/s,L0 =300.00 m
接下来,保持步进拟合时长b 不变,通过延长分段时长a 来观察积累时间变化对2 种方法性能的影响。所用参数为表1中的第1 组和第2 组参数,从图6和图7可以看出:
1)由于恒幅chirp 信号模型比恒幅恒频信号模型更适合于分段时长的提高,所以在较低信噪比时,FRFT-MDM 算法的积累效果要明显优于FFT-MDM算法。而信噪比较高时,噪声的影响相对较弱,所以这时的积累效果就相对不那么明显了;
2)当多普勒频率的变化率较小时,分段时长能够设置得较大些以获得更大的积累增益;而多普勒频率变化较为剧烈时,则通过增大分段时长来提升积累增益的效果就不明显了。这一点从表3的多普勒频率拟合误差均值也能够得到验证。可以看到第1组参数所对应的误差均值在分段时长超过2 帧后就没有明显的降低了,甚至还有所增大;而第2 组参数所对应的误差均值则基本保持与分段时长成反比。

表3 FRFT-MDM 算法的多普勒频率拟合误差均值Tab.3 The mean of estimation error of Doppler frequency using the FRFT-MDM algorithm

图6 SNR=0 dB 时测量误差与分段时长的关系Fig.6 The relationship between the measurement error and the segment with the SNR equaling 0 dB
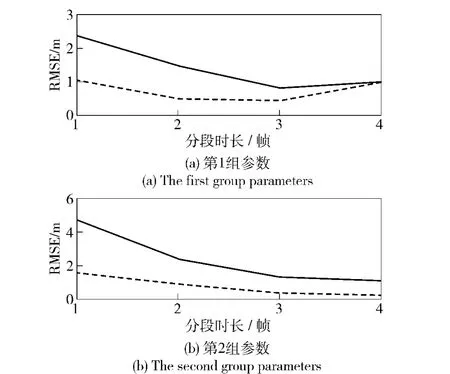
图7 SNR=-10 dB 时测量误差与分段时长的关系Fig.7 The relationship between the measurement error and the segment with the SNR equaling -10 dB
4 结论
1)在较低信噪比时,基于恒幅chirp 信号模型的FRFT-MDM 算法积累效果要明显优于FFT-MDM算法。在信噪比较高时,噪声的影响相对较弱,所以这时的积累效果不明显;
2)当多普勒频率的变化率较小时,分段时长能够设置得较大些以获得更大的积累增益;多普勒频率变化较为剧烈时,则通过增大分段时长来提升积累增益的效果不明显。
References)
[1]周宇翔,魏国华,吴嗣亮.基于窄脉冲的标量脱靶量测量算法[J].系统工程与电子技术,2007,29(2):196 -196.ZHOU Yu-xiang,WEI Guo-hua,WU Si-liang.Measurement algorithm of scalar miss distance based on narrow pulse[J].Systems Engineering and Electronics,2007,29(2):196 -196.(in Chinese)
[2]李志宇.矢量脱靶量测量数据处理方法的研究[D].北京:北京理工大学,2007.LI Zhi-yu.A study of data processing method for vector miss distance measurement[D].Beijing:Beijing Institute of Technology,2007.(in Chinese)
[3]吴嗣亮.矢量脱靶量测量系统数据处理方法的研究与实践[D].北京:北京理工大学,1998.WU Si-liang.Study on data processing technique for vector miss distance measurement system and its practice[D].Beijing:Beijing Institute of Technology,1998.(in Chinese)
[4]李志宇,吴嗣亮,魏国华.一种快速的矢量脱靶量测量算法[J].现代防御技术,2007,35(5):63 -66.LI Zhi-yu,WU Si-liang,WEI Guo-hua.Measurement of vector miss distance based on LFM signal model[J].Modern Defense Technology,2007,35(5):63 -66.(in Chinese)
[5]马淑芬,毛二可,侯舒娟.基于多普勒小波变换的脱靶量参数提取方法[J].北京理工大学学报,2006,26(12):1081-1085.MA Shu-fen,MAO Er-ke,HOU Shu-juan.Method of missile miss-distance parameters based on dopplerlet transform[J].Transactions of Beijing Institute of Technology,2006,26(12):1081 -1085.(in Chinese)
[6]TAO Ran,DENG Bing,WANG Yue.Research progress of the fractional fourier transform in signal processing[J].Science in China (Ser.F,Information Science),2006,49(1):1 -25.
[7]QI Lin,TAO Ran,ZHOU Si-yong,et al.Detection and paramter estimation of multicomponent LFM signal based on the fractional Fourier transform[J].Science in China (Ser.F,Information Science),2004,47(2):184 -198.
[8]TAO Ran,ZHANG Feng,WANG Yue.Research progress on discretization of fractional Fourier transform[J].Science in China(Ser.F,Information Science),2008,51(7):859 -880.
[9]Ozaktas H M,Arikan O,Kutay M A,et al.Digital computation of the fractional Fourier transform[J].IEEE Trans.Signal Processing,1996,44(9):2141 -2150.
[10]邓兵,陶然,杨曦.分数阶Fourier 域的采样及分辨率分析[J].自然科学进展,2007,17(5):655 -661.DENG Bing,TAO Ran,YANG Xi.The analysis of sampling and resolution in the fractional Fourier domain[J].Natural Science Progress,2007,17(5):655 -661.(in Chinese)
[11]赵兴浩,邓兵,陶然,等.分数阶傅立叶变换数值计算中的量纲归一化研究[J].北京理工大学学报,2005,25(4):360 -364.ZHAO Xing-hao,DENG Bing,TAO Ran,et al.Dimensional normalization in the digital computation of the fractional Fourier transform[J].Transactions of Beijing Institute of Technology,2005,25(4):360 -364.(in Chinese)

