金属球在转台逆合成孔径雷达成像中的应用

赵京城，洪韬

(北京航空航天大学电子信息工程学院，北京100191)

0 引言

在目标RCS(雷达散射截面)测试中，金属球、平板经常被用作标准体［1-4］。金属球作为标准体有明显的优势，其RCS 随频率升高趋于恒定值，给计算带来很大方便。在球坐标系中金属球是一维目标，具有旋转对称性，不存在由于定标体摆放姿态不准而产生的测量误差，这是圆柱、角反射器等定标体无法比拟的。

转台ISAR 成像可以得到目标散射源在旋转平面内的二维投影，对于目标的散射源诊断有重要意义。随着隐身技术的进步，转台ISAR 成像在散射测量中的作用越来越大。隐身飞机的研制通常要将总体RCS 指标分解到各个部件，例如座舱、进气道、雷达舱等。当某个方位的总RCS 测量值不满足设计指标时，就需要通过转台ISAR 成像来确定主要的散射源，从而采取有针对性的措施来减小主要散射源的影响，以达到设计要求。

本文通过金属球、金属平板的ISAR 成像和光学像在以旋转中心为原点的同一坐标系下的比对，修正了用金属球定标的转台ISAR 成像公式，对目标上弱散射源的准确定位非常有用。

1 转台ISAR 成像原理

转台ISAR 成像需要进行宽带测量，在每一个测试角度上，获得宽带信号的幅度和相位，积累一定角度范围的数据后就可进行ISAR 成像。转台ISAR成像的基本几何关系如图1所示:

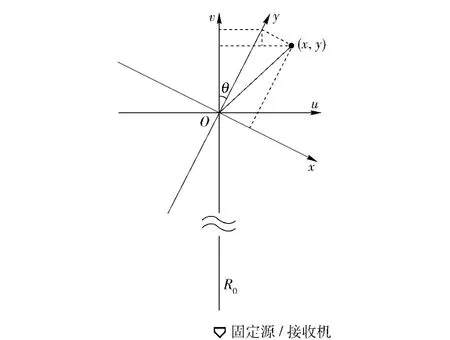
图1 目标空间坐标变换关系Fig.1 Coordinates transformation of target space

雷达天线固定于某一位置不动，目标绕旋转中心O 旋转，图1中u-v 坐标系是相对于雷达天线固定的，其坐标原点为目标旋转中心O，雷达到旋转中心的距离R0为一常数。x-y 坐标系是固定于目标上的一组坐标，它随目标旋转而旋转，坐标原点同样在O 点上。

雷达发射单频信号，频率为f，总的接收信号为

金属球通常被认为是点目标，其反射率分布为

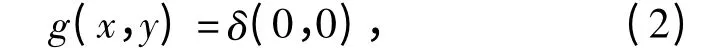
其相应的接收信号为

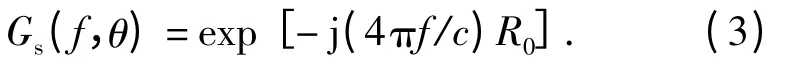
实用的宽带测试系统都会存在某种频率特性，这会影响成像的质量。因此，进行成像处理前，目标数据要与标准球的数据相比以消除系统频率特性，相比之后的数据变为

令k=2f/c，则

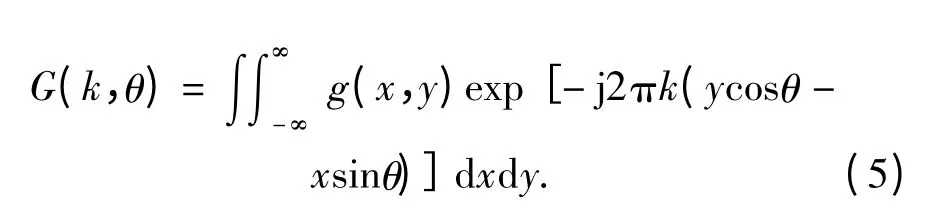
对G(k，θ)作二维逆傅立叶变换，便得到目标图像的估值:

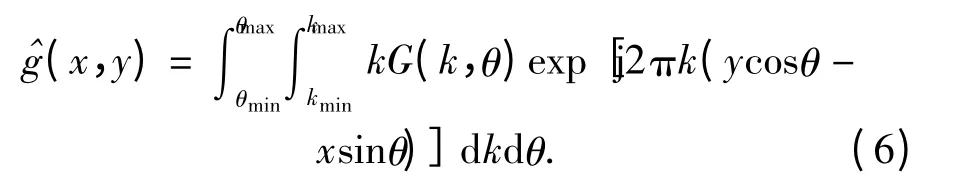
此式即为基本成像公式，实际上是一个极坐标格式的二维傅立叶变换，目前尚无极坐标格式的快速傅立叶变换算法，所以此积分采用CT 技术中的滤波-逆投影算法来进行计算［5］。

2 实际ISAR 成像遇到的问题

按照1 中给出的基本成像公式，由于假设金属球是点目标，且认为其反射率分布由式(2)给出。所以，对金属球进行ISAR 成像时，其散射中心必然位于旋转中心。但是，对金属球和金属平板进行ISAR 成像的结果却说明，推导ISAR 成像基本公式时对金属球反射率分布的假设存在一点问题。

对RCS 值为-15 dBsm 的金属球和长宽都为300 mm 的金属平板进行ISAR 成像，金属球和金属平板都摆放在目标支架的中心，其中金属平板垂直于电磁波照射方向，摆放位置见图2.

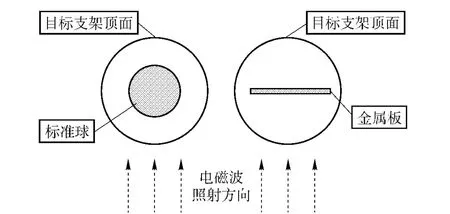
图2 金属球与金属平板摆放位置Fig.2 Position of a metallic sphere and plate

进行ISAR 成像测量，结果见图3.

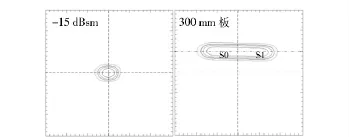
图3 金属球与金属平板二维像Fig.3 2-D image of a metallic sphere and plate

比较金属球和金属平板的成像结果，可以发现，金属球的ISAR 像位于成像中心，而金属平板的ISAR 像位于成像中心偏后0.1 m 的位置。由此可以推断，摆放在转台中心的金属球和金属平板散射源位置并不相同。从散射机理分析，金属平板属于镜面反射，其在旋转平面内的投影是一条直线。由于金属平板摆放在转台中心，其投影线必然经过转台的旋转中心。从转台二维成像的公式推导看，旋转中心应该就是成像中心。也就是说，金属平板的ISAR 像应该位于成像中心。从上图的比较结果看，金属球和金属平板的ISAR 像在距离方向上相差0.1 m，这个距离刚好是金属球的半径。很容易据此推断，金属球的散射中心并非位于其几何中心——球心，而是位于正对电磁波照射方向的顶点。Eugene F Knott 在“Radar Cross Section Measurements”一书中也指出，金属球的散射是由近表面的镜面反射和越过阴影区的爬行波构成［6］。对RCS 值分别为-10 dBsm、-15 dBsm、-20 dBsm 的金属球进行转台ISAR 成像，见图4.

图4 3 种不同尺寸金属球Fig.4 three metallic spheres of different size

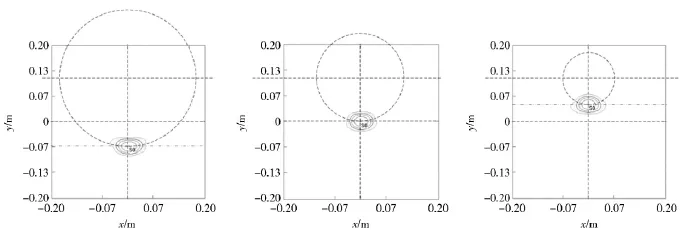
图5 3 种不同尺寸金属球的二维像Fig.5 2-D image of three metallic spheres

3 个金属球转台ISAR 像的散射中心坐标分别是-10 dBsm(0，-0.07)、-15 dBsm(0，0)、-20 dBsm(0，0.04)，见图5.

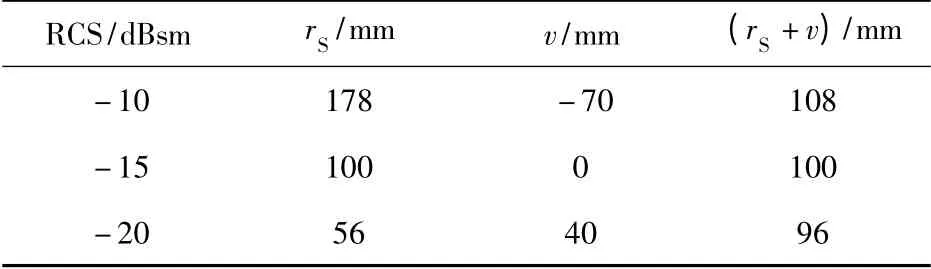
表1 3 种金属球散射中心位置Tab.1 Scattering center of three metallic spheres

3 个金属球几何中心都在旋转中心，而3 个金属球各自散射中心与半径的和都为100 mm(对应旋转中心坐标)，误差小于10 mm，这就印证了金属球散射中心在正对电磁波照射方向顶点的判断。

3 对ISAR 成像定标处理公式的修正

出现上面问题的原因在于金属球的反射率分布按照公式(2)的假设给出。我们已经知道，金属球的散射中心位于近表面的顶点。只要摆放时将金属球的几何中心置于(0，-rS)处，式(2)的反射率假设就成立。但是，这样会给金属球的摆放带来很大麻烦，尤其是当需要使用不同尺寸标准球的时候。所以，考虑将金属球的几何中心仍然置于旋转中心，而将其反射率分布做一下修正。

坐标系仍然按照图1中的坐标系，根据2 中的分析，金属球的散射中心位于正对电磁波照射方向的顶点。由于偏离坐标原点，其反射率分布在x-y坐标系和u-v 坐标系中会有不同表达式，为方便其见，在u-v 坐标系中表示。

式中，rS表示金属球的半径。

将式(7)代入接收信号的表示式中，重新推导目标图像的估值公式，可以得到:

此式即为修正后的基本成像公式，与修正前相比多了一个金属球的半径项。

用不同尺寸的金属球做标准体需要根据金属球的实际尺寸进行相应调整，如果已知金属球的RCS值，可以用简单公式计算得到金属球的半径。

式中，rS为金属球的半径，σ 为金属球的RCS 值。

用修正后的公式进行ISAR 成像处理，RCS 值为-15 dBsm 的金属球和长宽都为300 mm 的金属平板进行ISAR 成像见图6.

图6 金属球与金属板修正后的二维像Fig.6 Corrected 2-D image of a metallic sphere and plate

结果表明，金属球的散射中心位于成像中心前一个半径的位置处，而金属板的散射中心则位于成像中心，这与金属球和金属板的实际摆放位置是一致的。

4 对ISAR 成像公式进行修正的意义

在隐身技术发展的初级阶段，飞机散射源特征比较明显而且散射量级很高。进行二维成像分析时，通常不需仔细分析即可判断散射源产生的位置和机理。

图7 飞机模型40°二维像Fig.7 2-D image of an airplane model at 40°azimuth angle

在图7中，可以清楚地看到机翼前缘、进气道等位置产生的散射。对于这样的二维成像图，由于机翼前缘的散射特征比较明确，可以采用机翼前缘作为两种图象的比对参考点。但是对于散射特征不太明显的二维成像图，就不能依靠人为判断散射特征来比对，而应该找到更为准确的方法。

现在，随着F-117、F-22、F-35 等一系列高性能隐身飞机的出现，传统强散射源已经得到有效抑制，目标总体散射量级明显降低，以前一些被强散射源掩盖的弱散射源浮出水面。现在的散射测量经常需要面对一些外观上不易引起重视的弱散射源，这也使高精度散射测量面对比较大的挑战。对于非典型弱散射源的分析，二维成像是非常重要的工具。对弱散射源的测量分析往往是先找出RCS 测量曲线中有明显突起的的方位角，然后在此方位角上进行二维成像测量，诊断造成RCS 曲线突起的散射源位置，进而分析其散射机理。这其中要用到的一个重要手段就是目标二维布局图与二维成像图的比对，如果能够将两种图象通过某种联系准确叠加到一起，很快就能分析出二维像中的散射源是由目标的哪个位置产生。

对2 幅图象来说，如果图象中心能够作为叠加参考点，会给比对工作带来很大方便。对于二维成像图和模型平面图来说，用中心作为参考点有很大的可能。因为二维成像是ISAR 成像，也叫转台旋转中心成像，也就是说二维成像图的中心应该是转台旋转中心。对于目标测量来说，理想情况下目标重心应该与转台旋转中心重合，这就为图象比对提供了一条思路。保持模型图与二维成像图的尺度一致，然后将模型图中重心位置与二维成像图的中心叠加到一起，就可以比对散射源分布与模型的真实部件分布。

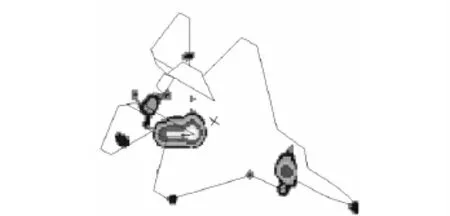
图8 飞机模型60°二维像Fig.8 2-D image of an airplane model at 60° azimuth angle

在图8中，可以清楚地看到模型上产生散射的位置，据此就可以采取有针对性的措施，降低目标总体散射。

使用修正后的ISAR 成像处理公式，准确控制模型的摆放位置，可以使处理得到的目标ISAR 像与目标投影图位置误差小于2 cm，基本可以满足散射源诊断的要求。

5 结语

本文根据经典ISAR 成像处理公式，使用金属球作为定标体进行成像测量，发现了成像中心与旋转中心不重合的问题。通过理论分析及实验验证，在金属球几何中心与旋转中心重合时，提出用金属球顶点作为散射中心，对ISAR 成像处理公式进行修正。用修正后的公式进行成像处理，可以获得准确的目标散射源分布，对真实目标的散射源诊断分析具有重要意义。

References)

［1］Lee T H，Clark T L，Burnside W D，et al.Critical range evaluation using a diagonal flat plate［J］.IEEE Transactions on Antennas and Propagation，1992，40(8):966 -974.

［2］Levitas B，Matuzas J.Indoor time domain RCS measurements and ISAR imaging without anechoic chamber［C］∥Jozef Modelski.15th International Conference on Microwaves，Radar and Wireless Communications MIKON-2004 (Volume 2).New York:IEEE，2004:686 -690.

［3］Solimene R，Buonanno A，Pierri R，et al.Localizing metallic small spheres by a linear distributional approach［C］∥Ignasi Corbella，Adriano Camps.IEEE International Geoscience and Remote Sensing Symposium IGARSS 2007.New York:IEEE，2007:350-353.

［4］Wei P S P，Reed A W，Ericksen C N.Two-sphere interference in RCS measurements and imaging［J］.IEEE Antennas and Propagation Magazine，2004，46(2):166 -172.

［5］黄培康.雷达目标特征信号［M］.北京:宇航出版社，1993.HUANG Pei-kang.Radar target’s signature［M］.Beijing:China Astronautic Publishing House，1993.(in Chinese)

［6］Eugene F Knott.Radar cross section measurements［M］.New York:Van Nostrand Reinhold，1993:177.