理念不同 教法各异——角平分线性质、判定定理的教法设计比较

吴 荣，汤逸平

（张家港市暨阳湖实验学校，江苏 张家港 215600；张家港市第三中学，江苏 张家港 215600）

理念不同 教法各异
——角平分线性质、判定定理的教法设计比较

吴 荣，汤逸平

（张家港市暨阳湖实验学校，江苏 张家港 215600；张家港市第三中学，江苏 张家港 215600）

近日因参加市骨干教师的全市课堂教学展示活动，我执教了华师大版数学九年级（下）——角平分线的性质定理、判定定理。通过精心研读教材、巧妙设计教学过程，上出了一节能体现新课程教育理念、得到所有听课老师好评的课。在整理听课老师的评课意见后，我特地把十年前同一内容的教案设计拿出来作了个比较，发现竟然有着明显的差别。真可谓理念不同，教法各异。现将两份教学设计的主要教学过程对比如下，并反思了我在新课程理念指导下的教学体会。

【现教学设计】

Ⅰ.设置情境问题，搭建探究平台

【问题】还记得角平分线上的点有什么性质吗?你是怎样得到的？

师生共同用折纸的方法很难验证角平分线上的点的性质。

[师]你能证明它吗？

Ⅱ.展示思维空间，构建活动空间

引导学生画图，并写出已知、求证。请同学们自己尝试着证明它，然后在全班进行交流.

（教师在教学过程中对有困难的学生要给以指导）

Ⅲ.活学活用

1.Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=8，BD=5，求点D到AB边的距离。

2.⊙O的圆心O在角平分线并且与角两边相交于点A、B和 C、D，求证：AB=CD

Ⅳ.换个角度，思考问题

我们经常用逆向思维，从它的反面看问题，也就是交换题设与结论，能得到什么呢？

[生]如果有一个点到角两边的距离相等，那么这个点必在这个角的平分线上。

[师]你能证明它吗？

（由大家自己独立思考完成，在全班讨论交流，对困难学生可个别辅导）

Ⅴ.你会画角平分线吗？

我们证明了角平分线的性质定理和判定定理，你能用什么办法平分一个已知角呢？请在小组内交流。

[生]可以用量角器；使用三角尺，也可以平分一个已知角；直尺和圆规；如果有角尺的话，用角尺也可以平分一个已知角。

利用其他工具呢？（在总结学生画的基础上，老师给出一些同学的画法，你看可以吗？）

练习：P39第1题

Ⅵ.活动与探究，相信你能行

1.在三角形内找一点，使这点到三边的距离相等，你找得到吗？（分析证明）

练习：P39第2题

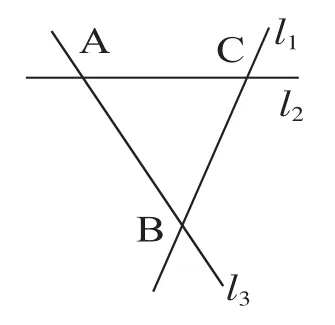
2.（变式训练）如图，直线 l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有几处？

3.请大家商量想办法，一起做一个简易的角平分线器。（教师提供若干根两种规格长度的木棒，木棒的两端可由螺栓连接）

【原教学设计】

Ⅰ.复习旧知

1.什么叫角平分线？

2.如图，OC是∠AOB的角平分线，可得到什么结论？

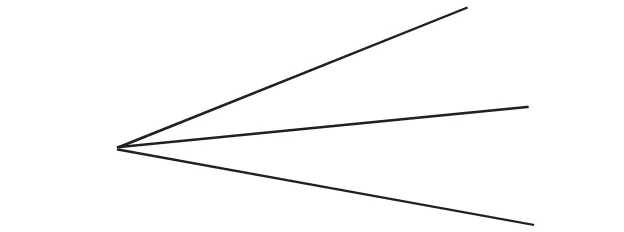
3.练习

如图，D是角平分线OC上一点，DE⊥OA于点E，DF⊥OB于点 F，求证：DE=DF。

Ⅱ.新授

1.角平分线性质定理

定理：角平分线的点到角两边的距离相等。

引导学生分析、画图、写出已知、求证并进行证明。（略）

2.如果交换一下条件与结论，会得到什么命题呢？它是真命题还是假命题？

[生]到角两边距离相等的点在这个角的平分线上。

学生自己画图、写出已知、求证，并写出证明的过程。（一位学生上黑板板演）总结板书角平分线的逆定理。

Ⅲ.巩固练习

1.△ABC的两个外角∠ABC、∠ABC的平分线交于点D，求证：D点在∠A的角平分线上。

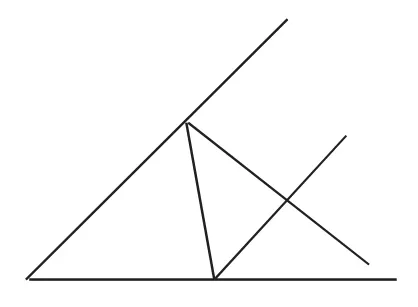
2.在△ABC的BC边上作一点D，使它到AB、AC的距离相等。

本节课是在学习了三角形全等的判定定理及等腰三角形的性质识别定理、判定定理的基础上进一步学习角平分线的性质和判定定理及相关结论。比较上述两份教学设计，我们不难发现现教学设计有如下特点：

1.问题来源于生活，学“有用的数学”

美国心理学家布鲁纳认为，在教学过程中，教师的作用是要形成一种使学生能够独立探究的情景，而不是提供现成的知识。因此在教学中，教师应努力创设具有启发性的问题情景，以问题的发现来激发学生的求知欲，并由此推动学生主动探究、寻求解决问题的方法的学习热情。通过用贴近学生生活的问题情景，如“Ⅵ.活动与探究，相信你能行”，对学生来说倍感亲切，觉得数学就在我们身边。再加上教师的指导点拨，更使得学生的求知欲望迅速高涨，从而促使学生怀着强烈的好奇心和迫切探究的心情与教师一起步入知识的殿堂。又如本课结束前的一问：请大家商量想办法，一起做一个简易的角平分线器。就会让学生体会到数学的价值所在。也印证了新课程倡导的理念：加强课程的实用性，课程不再被驾空于生活之上，它必须回到它所滋生的土壤——生活中去。而原教学设计在这一点上做得是很不够的。

2.授之于“鱼”，不如授之于“渔”

在原教案中，教师注重的是知识的讲授，学生注重的是知识的接受。教师千方百计地想把问题讲清楚，通过“讲-练-评”这一程式，传授知识。而在新课程理念的指导下，教师在教学过程中，更重视的是学习方法的指导，特别重视知识的发生发展的过程，而不仅仅是结论。改变了过去“闭门造车”式的独立学习为讨论、研讨探究式的合作学习而，鼓励学生“敞开说”，敢于发表自己的见解。提倡争议、相互启发，提高认识、完善发现，这对提高学生的探究问题的能力、思维能力、表达能力和组织能力等具有不可低估的作用。

如本课中就不止一次地要求学生先独立思考作答，再小组或全班交流。由于学生已探索过角平分线的性质，而此处在学生回忆的基础上，让学生尝试着证明它，并进行交流；再利用不同的工具画平分线后交流；进一步讨论三角形三个内角平分线的性质等等，如果仅仅是个人或老师直接讲解，效果就远不如讨论、交流、共同探索的效果好。

3.尊重学生认知规律，归纳、揭示本质

课程标准在“知识技能目标”中，明确提出较高的目标是灵活运用。能综合运用数学知识，灵活、合理地选择与运用有关的方法完成特定的数学任务。经常训练学生的概括能力、透过现象看本质是实现这一目标的好办法。由于初中学生的年龄特点，在对知识进行归纳、揭示本质过程中，应尊重学生的认知规律，从学生已有的知识与经验出发，先感性认识再上升到理性认识。

如新教学设计对角平分线性质定理的证明，就采用“实验验证——证明猜想”的教学方法。由于学生初学角平分线的性质定理和判定定理，容易将角平分线上的一点到这个角两边的距离误认为过这点垂直于角平分线的垂线段。因此在教学中应首先让学生通过画三角形纸片的折痕来充分认识这一点。先让学生通过折纸感性理解这一性质，再适时启发诱导，让学生展开讨论，完成证明的书写。这样做的好处在于：学生的主体参与意识得到了充分发挥，也活跃了课堂气氛，并从中提高了归纳问题、揭示本质的本领。

另外，新教学设计中淡化了课程的工具性色彩，知识性因素不再是唯一的基调；课程的人文色彩这个被传统忽略的因素被重重地抹在我们的新教案设计之中，成为不可忽略的因素。如本节教学设计中就不止一次地出现了“你能证明它吗？相信你能行”这样人性化的提问。这与原教学设计显然有着明显的差别。

张华伟）