三维极限平衡法通用形式的建立及应用

张常亮,李同录,李 萍

(长安大学地质工程与测绘学院,陕西西安710054)

0 引言

随着极限平衡法的发展,众多学者[1-23]逐渐发现,针对边坡的稳定性分析应该从三维而不仅仅是二维的角度来进行,因为他不仅能带来分析精度的提高,也可以使支挡设计上更经济安全,而且当前计算机技术的发展也使三维稳定分析中繁琐的计算得以实现。

截止目前,三维极限平衡法的研究已取得一些成果,如 Hovland[1]在 Fellenious法的基础上提出了三维条柱法;Hungr等[2-3]先后将Janbu法和Bishop法扩展到三维;Zhang[4]提出了三维 Spencer法;陈祖煜等[5]提出了三维 Morgenstan-Spencer法;李同录等[6]提出了三维简化 Sarma法。可以看出,与二维极限平衡法相比,三维领域极限平衡理论的发展还远未成熟,尽管许多学者提出了一系列三维边坡极限平衡方法,但迄今为止,还没有开发出一个在工程界可广泛应用的三维边坡稳定分析程序。因此,在三维极限平衡法研究方面做进一步的探讨具有很重要的实际意义。

基于边坡整体力平衡、力矩平衡以及边坡微条柱力平衡,笔者提出了一个综合各种三维极限平衡法的通用形式,该通用形式包含3个表达式,通过这3个表达式利用原方法的假定条件就可以得到原方法的表达形式,并将他们解析化,不仅大大降低了传统三维极限平衡法的计算工作量,还使计算精度大为提高。

1 通用形式建立

如图1,取主滑方向为x坐标,垂直滑动方向的边坡走向方向为y坐标,竖直向上为z坐标,x、y、z符合右手法则。现取 x方向长度为dx,y方向长度为dy的微条柱进行分析(图2)。微条柱共有6个面,除顶面外,每个面受3个力的作用,即2个剪切力和1个垂直力。N代表垂直力,用下标表示作用面,如Ny代表法线为y的面上的垂直力;T代表剪切力,T的第1个下标表示作用面,第2个下标代表力的方向,如 Tyx代表法线为y的面在x方向上受的剪切力。dN和dT分别代表法向力和剪切力的微分增量。dTz代表微条柱底滑面的剪切力, dNz代表微条柱底滑面的法向力,dW代表微条柱的体积力。ax表示底滑面相交于xOz平面的线和水平面之间的夹角;ay表示底滑面相交于yOz平面的线和水平面之间的夹角。

图1 边坡三维稳定性分析模型Fig.1 Three-dimensional Analysis Model of Slope

1.1 基本假设

该通用形式基于以下假定条件:

(1)稳定系数定义为材料的强度折减系数。

(2)土体为刚体,底滑面服从 Mohr-Coulomb强度破坏准则

式中:fφ=tanφ/F,fc=c/F;φ为底滑面处的内摩擦角;c为底滑面处的内聚力;F为稳定系数;u为孔隙水压力;dAz为微条柱底滑面的面积。

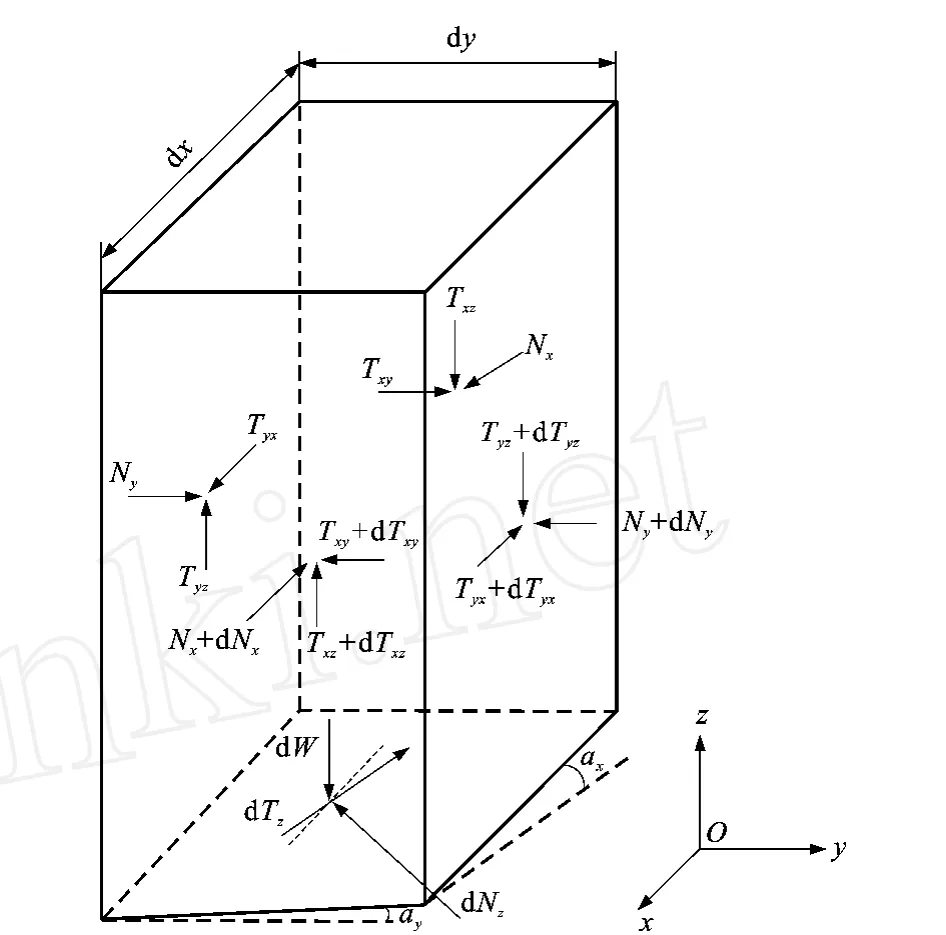
图2 微条柱受力Fig.2 Forces on Differential Column

1.2 通用形式的建立

三维极限平衡法的通用形式包含3个表达式,他们分别通过满足边坡的整体力平衡、整体力矩平衡以及微条柱的力平衡来获得。

当从边坡整体力或力矩平衡来分析其稳定性时,所有内力的作用均在内力的相互作用中抵消了,也就是说,这个时候微条柱4个侧边的所有内力均不需要考虑,这样,就剩下微条柱的体积力dW、底滑面上的法向力dNz和剪切力dTz这3个力。通过这3个力沿空间任一条直线的力平衡和绕空间任一直线的力矩平衡,就可以得到通用形式中的前2个表达式,具体过程如下:

设dNz的方向余弦为(nx,ny,nz),dTz的方向余弦为(lx,ly,lz);任取一方向余弦为(mx,my,mz)的空间直线,将以上3个力投影到该直线,建立这些投影的力平衡则可得

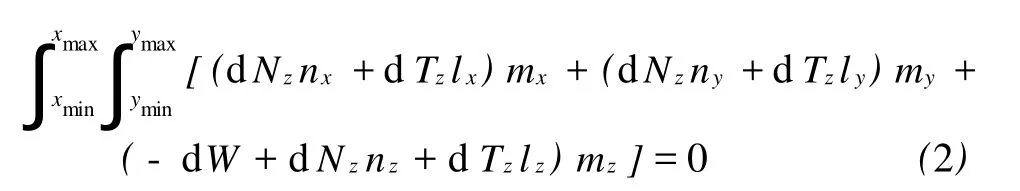
将式(1)代入式(2),整理可得

式中:G1=lxmx+lymy+lzmz

G2=nxmx+nymy+nzmz

式(3)即为通用形式中第一个表达式。

再任取一方向余弦为(Rx,Ry,Rz),方向正弦为(Sx,Sy,Sz),且过点(xm,ym,zm)的直线,将该直线作为旋转轴,将上述3个力先沿 x、y、z轴分别投影,再将这些投影值投影在该直线的垂直面上,最终的投影值的合力与该直线的距离(力臂)分别为dx、dy、dz(图3),根据几何关系可知

则

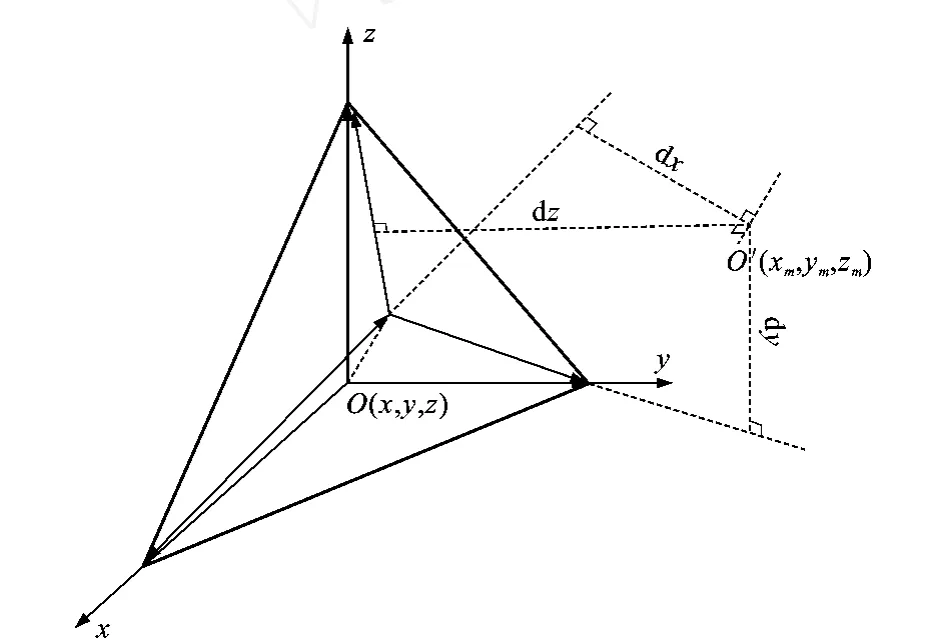
图3 力矩力臂几何关系Fig.3 G eometrical Relationship Between Arm and Moment

这样,通过建立这些投影值绕该直线的力矩平衡可得

将式(1)代入式(4),整理可得

式中:G3=lxSxdx+lySydy-lzSzdz

G4=nxSxdx+nySydy-nzSzdz

式(5)即为通用形式中第二个表达式。

式(3)和式(5)中只包含 F和dNz这2个未知量,只要确定dNz的表达式,就可以确定 F。由于dNz都是通过微条柱上所有力的力平衡来获得的,为此,与建立第一个表达式时一样,先任取一方向余弦为(vx,vy,vz)的空间直线,将作用在微条柱上的所有力投影到该直线,建立它们的力平衡,可得

将式(1)代入式(6),整理可得

式中:G5=lxvx+lyvy+lzvz

式(7)即为通用形式中第三个表达式。该式中还包含一些未知量,如dNx、dNy、dTxy、dTyx、dTxz、dTyz。他们均可根据不同模型的假定条件来确定。

这样,包含式(3)、(5)、(7)这3个表达式的三维极限平衡法的通用形式就此建立。

2 其他方法的推导

2.1 三维普通条分法

该模型由 Hovland[1]将二维分析法中的普通条分法(Fellenious)扩展为三维条柱法推导而来。它忽略了条柱间所有剪切力和法向力,同时使底滑面上的剪切力与主滑方向平行,也就是忽略了平行于 yOz平面的剪切力dTzy。然后,在沿滑面力平衡的基础上得到了稳定系数的表达式。这样,就需要通过通用形式中的式(3)和式(7)对其进行推导。

由假设条件可知:

将以上条件代入式(3),整理可得

将以上条件代入式(7),整理可得

式(8)即为三维普通条分法的解析形式,式(9)为该方法dNz的表达式。

2.2 三维简化Janbu法

该模型由 Hungr等[2]建立,它忽略了条柱间沿z轴方向的所有剪力,同时使底滑面上的剪切力与主滑方向平行,即忽略了平行于yOz平面的剪切力dTzy。在此假设条件下,通过每一微条柱竖向力的平衡以及滑体沿x轴整体的力平衡,建立了求解稳定系数的表达式。这样,也就需要通过通用形式中的式(3)和式(7)来对其进行推导。

由假设条件可知

将以上条件代入式(3),整理可得

将以上条件代入式(7),整理可得

式(10)即为三维简化Janbu法的解析形式,式(11)为该方法dNz的表达式。

2.3 三维简化Bishop法

该模型由 Hungr[3]建立,是二维简化Bishop法的直接扩展。他也忽略了条柱间沿 z轴方向的所有剪力,同时也使底滑面上的剪切力与主滑方向平行,即忽略了平行于 yOz平面的剪切力 dTzy。在此假设条件下,通过每一微条柱竖向力的平衡以及滑体绕y轴的整体力矩平衡,建立了求解稳定系数的表达式。这样,就需要通过通用形式中的式(5)和式(7)来对其进行推导。

由假设条件可知

将以上条件代入式(5),整理可得

将以上条件代入式(7),整理可得

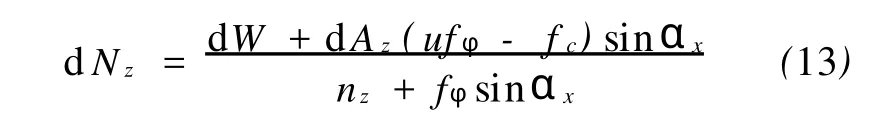
式(12)即为三维简化Bishop法的解析形式,式(13)为该方法dNz的表达式。

2.4 三维Morgenstern-Spencer法

该模型由陈祖煜等[5]建立,是二维 Morgenstern-Spencer法在三维条件下的扩展。他忽略了作用在平行于xOz平面条柱侧面上的剪切力;忽略了作用在平行于 yOz平面条柱侧面上的水平剪力,并使法向力 Nx与竖向剪力Txz的合力G与x轴的夹角为β;同时,使作用在底滑面上的剪切力dTz与xOz平面的夹角为ρ,并规定剪切力的 y轴分量为正时ρ为正值,dTz的方向余弦为(lx,ly,lz),且lz=sinρ。在此假设条件下,通过 G和y轴方向上的整体力平衡,以及绕y轴的整体力矩平衡建立了3个求解稳定系数的表达式,这样,就需要分别通过通用形式中的式(3)、(5)、(7)来对其进行推导。

(1)沿 G方向的整体力平衡。由几何关系可知,在该方向上

将以上条件代入式(3),整理可得

(2)沿y轴方向的整体力平衡。由几何关系可知,在该方向上

将以上条件代入式(3),整理可得

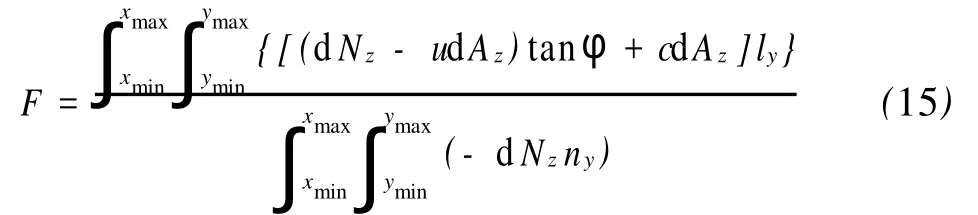
(3)绕y轴的整体力矩平衡。由几何关系可知

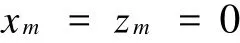
将以上条件代入式(5),整理可得

3个方程中所包括的未知量dNz可以通过与G垂直方向上的力平衡得到,由该模型的几何关系及假定条件可知

将以上条件代入式(7),整理可得

式(14)～(16)即为三维Morgenstern-Spencer法的解析形式,式(17)为该方法dNz的表达式。

2.5 三维简化Sarma法

该方法由李同录等[6]建立,为二维Sarma法的三维扩展。他忽略了作用在平行于平面 yOz界面上的水平向剪力;假定平行于xOz平面界面上条间剪力与底滑面平行;使作用在底滑面上的剪切力dTz与xOz平面的夹角为ρ,并规定剪切力的 y轴分量为正时ρ为正值;同时,假定底滑面和条柱侧面均满足Mohr-Coulomb准则,并均具有相同的抗剪强度指标φ和c,以及相同的稳定系数。在此假设条件下,通过沿x轴的整体力平衡建立了求解稳定系数的表达式,通过沿 x、y、z轴3个方向的力平衡建立了dNz的求解公式,这样,就需要分别利用通用形式中的式(3)和式(7)来对其进行推导。

因为该模型满足沿x轴方向的整体力平衡,则

将以上条件代入式(3),整理可得

式(18)中所包括的未知量dNz需在微条柱同时满足x、y、z轴3个方向的力平衡情况下得到,由该模型假定条件可知

式中:dAx为微条柱平行于yOz平面的侧面的面积;dAy为微条柱平行于xOz平面的侧面面积。

(1)微条柱沿 x轴方向的力平衡。根据几何条件可知

将以上条件代入式(7),整理可得

(2)微条柱沿y轴方向的力平衡。根据几何条件可知

将以上条件代入式(7),整理可得

(3)微条柱沿z轴方向的力平衡。根据几何条件可知

将以上条件代入式(7),整理可得

联立式(19)～(21),消去内力dNx、dNy,整理可得

式中:

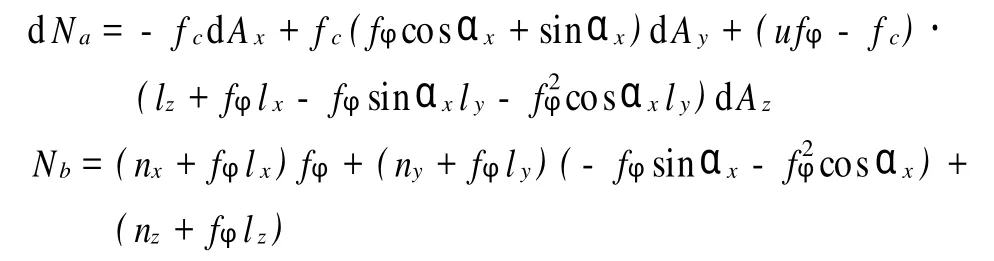
式(18)即为三维简化Sarma法的解析形式,式(22)为该方法dNz的表达式。

3 算例

图4为Zhang[4]提供的旋转椭球体滑面例题,图5为概算例三维示意图。国内外很多学者都选择本例题来检验各自三维程序的合理性。笔者亦采用这一经典算例所提供的地面数据及物理力学指标来分析由通用形式导出的各模型解析形式的合理性和各参数对三维边坡稳定性的影响。

图4 Zhang的算例Fig.4 Case from Zhang

由图4可知,坡体为一均质土坡,坡体土天然重度γ为19.2 kN/m3,抗剪强度指标φ为20°、c为29.3 kN/m2,纵向半径 Ra为24.4 m。

3.1 滑体宽度对稳定系数的影响

一般认为,当滑体的横向宽度远大于其沿主滑动方向的长度时,边坡的稳定性分析为平面应变问题,即二维问题;而当滑体比较狭长时,其三维效应就非常明显,必须作为空间问题来考虑。

图5 算例三维图Fig.5 Three-dimensional Shape of Case

为了检验各模型是否满足上述观点,这里取该旋转椭球体的纵向半径 Ra来反映滑体的长度,取横向半径Rb来反映滑体的宽度。

先固定中轴面,使纵向半径 Ra=24.4 m,然后令Rb和 Ra的比值分别为0.5、1、1.5、2、2.5、3、4、6、8、12,采用通用形式推导来的三维普通条分法(GM)、三维简化Bishop法(SBM)、三维简化Janbu法(SJM)、三维Morgenstern-spencer法(MSM)以及三维简化Sarma法(SSM)的解析形式进行稳定性验算,其结果如表1。

表1 滑体宽度对稳定系数的影响Tab.1 Affection of Sliding Body Width on Safety Factor

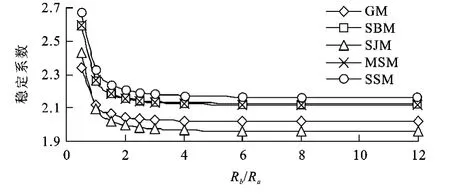
从图6可以看出,无论采用何种方法,当 Rb/ Ra小于2时,稳定系数很大,而随着两者比值的增大,即滑体的横向宽度远大于其沿滑动方向的纵向长度时,稳定系数逐渐变小。当 Rb/Ra大于2时,稳定系数的变化逐渐减缓,在 Rb/Ra大于4以后,几乎不再变化,此时,边坡稳定问题接近于二维的平面应变问题。为此,可以得出如下结论:当滑体比较狭长,尤其是 Rb/Ra小于2时,侧向作用对边坡的稳定性有很大的影响,滑体的三维效应非常明显,此时的边坡稳定问题,必须作为空间问题来考虑;当滑体横向上较宽,尤其是在 Rb/Ra大于4时,侧向作用对边坡稳定性的影响微弱,此时的空间问题可作为二维问题来考虑。

同时,从表1可以看出,由于普通三维条分法因没有考虑侧向力,稳定系数偏小;三维简化Sarma法由于假定条柱除顶面外均处于极限平衡状态,稳定系数较大;Hungr所提出的三维简化Bishop法,由于考虑了条间侧向力对稳定系数的影响以及考虑了力矩平衡,所得的稳定系数较普三维条分法有较大的提高,他提出的三维简化Janbu法则因只考虑力平衡而使得获得的稳定系数偏小。三维Morgenstern-Spencer法由于考虑了力矩平衡,其所得的稳定系数偏大。

3.2 滑面强度参数对稳定系数的影响

滑面的强度参数对稳定性的影响非常重要,在二维极限平衡法中,φ值由于同滑体的重力有关系,因此对稳定系数的影响较大。这里对三维方法也进行验算。为此,以 Rb为36.6 m的算例为例,先给定φ值,使φ=20°,研究c对稳定系数的影响;再给定c值,使c=29.3 kN/m2,研究φ值对稳定系数的影响。其结果如图7、8。

图7 滑面内聚力与稳定系数关系曲线Fig.7 Relationship Between Cohesion Force and Safety Factor

由图7、8可以看出,无论采用何种计算方法,随着φ和c的增大,稳定系数都呈近线性增加趋势,但φ对稳定系数的影响要明显高于c。这是由于c值所发挥的抗滑作用仅与滑动面面积有关,与滑动面形状和上覆荷载无关,而φ值产生的抗滑作用则与滑动面形状、上覆荷载和面积都有很大关系,滑动面越缓,上覆土层越厚,体积越大,φ值发挥的抗滑力越大。

图8 滑面内摩擦角与稳定系数关系曲线Fig.8 Relationship Between Internal Friction Angle and Safety Factor

3.3 滑面剪力方向对稳定系数的影响

对于考虑滑裂面剪力方向对稳定系数影响的三维 Morgenstern-Spencer法和三维简化 Sarma法,滑面剪力方向与底滑面和xOz平面交线的夹角ρ的取值结果直接关系到两种方法稳定系数的最终计算结果,而对该值到底是以常数的形式取值还是以函数的形式更合适,目前相关的研究也没有一个明确的结论。为了充分了解滑面剪力的方向对稳定系数的影响,将ρ按2种情况分别计算分析。这里均以 Rb为36.6 m的算例为例进行相应分析。

(1)ρ=常数。将ρ取为常数,也就是将整个滑体滑裂面上的剪力取为一个方向,其取值范围为[-60°,60°],稳定系数计算结果如表2。

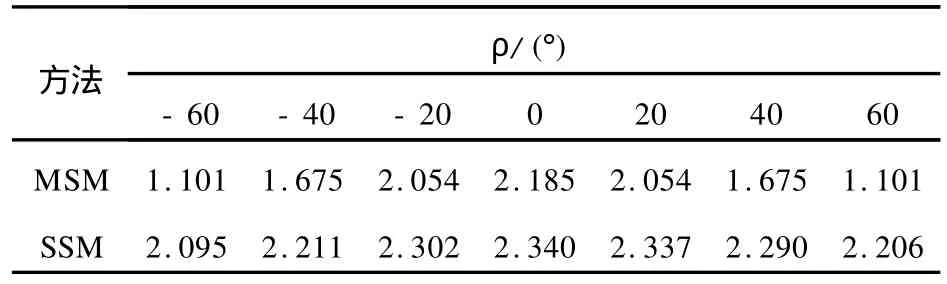
表2 在ρ为常量情况下剪切力方向对稳定系数的影响Tab.2 Affection of Shearing Force Direction on Safety Factor ifρwas Constant

由表2及图9可以看出,当ρ为正时,稳定系数 F随着它的增大不断减小,当ρ为负时,稳定系数 F则随着它的增大不断增大,在ρ=0这个位置上,稳定系数达到最高值。这一结果可用潘家铮[24]的最大原理来解释。当滑坡体的滑面确定时,滑面上的反力(以及滑体的内力)能自行调整,以发挥最大的抗滑力,最大抗力出现在与滑动方向相反的角度上。

图9 在ρ为常量情况下剪切力方向与稳定系数关系曲线Fig.9 Relationship Between Shearing Force Direction and Safety Factor ifρwas Constant

(2)ρ以函数分布。对于对称边坡,当采用分布函数ρ=f(y)=0.5λ(y-y0)/Rb(λ为控制变量, 0°≤λ≤90°;y0为滑坡主滑断面的 y坐标值)时,可得到表3的计算结果。

表3 在ρ为变量情况下剪切力方向对稳定系数的影响Tab.3 Affection of Shearing Force Direction on Safety Factor ifρw as V ariable

由表3及图10可以看出,稳定系数随着λ的不断增大而减小,当λ=0时,稳定系数最大,这一结果同样可用潘家铮[24]的最大原理来解释。

图10 在ρ为变量情况下剪切力方向与稳定系数关系曲线Fig.10 Relationship Between Shearing Force Direction and Safety Factor ifρw as V ariable

对于一般滑体,考虑将滑裂面剪切力方向与其底面倾向相互关联起来,在滑体主滑段取其方向与底面倾向相反,反翘段取与底面倾向一致。在该条件下,三维Morgenstern-Spencer法求得的稳定系数为2.185,三维简化Sarma法求得的稳定系数为2.241。

由计算结果可以看出,将滑裂面剪切力方向取为与其底面倾向相关计算出的结果与文献[5]的考题1计算结果相差不大,比较接近实际情况。

4 结语

(1)在满足边坡整体力平衡、力矩平衡以及边坡微条柱力平衡的条件下,提出了一个综合各种三维极限平衡法的通用形式,该通用形式包含3个表达式。

(2)通过所建立的通用形式,利用已有方法的假定条件推导出了原方法的表达形式,并将它们解析化。

(3)通过Zhang的算例,利用通用形式导出的三维普通条分法、三维简化Janbu法、三维简化Bishop法、三维Morgenstern-Spencer法以及三维简化Sarma法的解析形式,分析了滑体宽度、滑面强度参数以及滑面剪切力方向对稳定系数的影响,结果表明,该通用形式是正确有效的。

[1] Hovland H J.Three-dimensional Slope Stability Analysis Method[J].Journal of the Geotechnical Engineering Division,1977,103(9):971-986.

[2] Hungr O,Salgado F M,Byrne P M.Evaluation of a Threedimensional Method of Slope Stability Analysis[J].Canadian Geotechnical Journal,1989,26(4):679-686.

[3] Hungr O.An Extension of Bishop's Simplified Method of Slope Stability Analysis to Three Dimensions[J].Geotechnique,1987,37(1):113-117.

[4] Zhang X.Three-dimensional Stability Analysis of Concave Slopes in Plan View[J].Journal of GeotechnicalEngineering,1988,114(6):658-671.

[5] 陈祖煜,弥宏亮,汪小刚.边坡稳定三维分析的极限平衡方法[J].岩土工程学报,2001,23(5):525-529.

[6] 李同录,王艳霞,邓宏科.一种改进的三维边坡稳定性分析方法[J].岩土工程学报,2003,25(5):611-614.

[7] Chen R H,Chameau J L.Three-dimensional Limit Equilibrium Analysis of Slopes[J].Geotechnique,1983,33(1):31-40.

[8] Hutchinson J N,Sarma S K.Discussion of Three-dimensional Limit Equilibrium Analysis of Slopes[J].Geotechnique, 1985,35(2):215-216.

[9] Leshchinsky D.Discussion of“Three-dimensional Stability Analysis of Concave Slopes in Plan View”[J].Journal of Geotechnical Engineering,1990,116(2):342-345.

[10] Leshchinsky D,Baker R,Silver M L.Three Dimensional Analysis of Slope Stability[J].International Journal for Numerical and Analytical Methods in Geomechanics,1985,9 (3):199-223.

[11] Leshchinsky D,Baker R.Three-dimensional Slope Stability: End Effects[J].Soils and Foundations,1986,26(4):98-110.

[12] Leshchinsky D,Huang C C.Generalized Three-dimensional Slope-stability Analysis[J].Journal of Geotechnical Engineering,1992,118(11):1748-1764.

[13] Cavounidis S.Discussion of An Extension of Bishop's Simplified Method of Slope Stability Analysis to Three Dimensions [J].Geotechnique,1988,38(1):155-156.

[14] Gens A,Hutchison J N,Cavounidis S.Three-dimensional Analysis of Slices in Cohesive Soils[J].Geotechnique,1988, 38(1):1-23.

[15] Ugai K.Three-dimensional Stability Analysis of Vertical Cohesive Slopes[J].Soils and Foundations,1985,25(3):41-48.

[16] 王志斌,李 亮,杨小礼,等.水平条分法在贴坡高填方路堤稳定性分析中的应用[J].中国公路学报,2007,20(3):14-19.

[17] 蒋 鑫,魏永幸,邱延峻.斜坡软弱地基路堤填筑全过程稳定性[J].交通运输工程学报,2003,3(1):30-34.

[18] 王文生,谢永利,梁军林.膨胀土路堑边坡的破坏型式和稳定性[J].长安大学学报:自然科学版,2005,25(1):20-24.

[19] 柳厚祥,廖 雪,李 宁,等.公路边坡稳定性分析的二维变分方法[J].中国公路学报,2007,20(4):7-11.

[20] 李 亮,王玉杰,郑榕明.局部安全系数法在土坡稳定分析中的应用[J].建筑科学与工程学报,2008,25(2):36-40.

[21] 苏永华,赵明华,李志勇,等.基于虚拟试验的边坡失稳概率分析方法[J].中国公路学报,2008,21(6):14-19.

[22] 徐世强,折学森,刘怡琳,等.公路黄土坝式路堤稳定性计算方法[J].交通运输工程学报,2006,6(3):42-46.

[23] 李 萍,王秉纲,李同录,等.陕西地区黄土路堑高边坡可靠度研究[J].中国公路学报,2009,22(6):18-25.

[24] 潘家铮.建筑物的抗滑稳定和滑坡分析[M].北京:水利出版社,1980.