高陡库岸滑坡初始涌浪波幅预测模型研究

柯 超，汪 洋，2*，霍志涛，张玉洁，刘继芝娴

(1.中国地质大学(武汉)工程学院，湖北 武汉 430074；2.三峡库区地质灾害野外监测与预警示范中心，重庆 404000;3.中南地质科技创新中心，湖北 武汉 4302052)

滑坡作为的一种常见的地质灾害，其所携带的巨大能量在撞击库区水体过程中传递给水体并引发不同形态、具有一定能量的涌浪。滑坡入水虽然是一个连续性过程，但是滑坡入水后能量传递时间十分短暂，且能量传递机理十分复杂。相对于低缓库岸滑坡，高陡库岸滑坡速度更快，入水后产生的涌浪相对更高，能量传递时间更短暂，破坏性更强。高陡库岸滑坡发生后以较快的速度最先对受灾体造成破坏，因此对高陡库岸滑坡影响范围区域特别是近场区域的初始涌浪进行研究和预测具有重要意义。

滑坡入水过程的涌浪能量传递研究大都通过滑体与水体体积、速度、动量守恒或者建立滑坡体与水体的流固耦合模型来寻求滑体能量和涌浪能量之间的关系。国内外学者在这方面做了大量的研究工作，但大多数只侧重于模型或者方法的建立，对滑坡入水后涌浪形成机制或者现象考虑较少，缺少一定的理论基础。在滑坡初始涌浪物理模型试验中，由于涌浪的波动能很难被监测到，一般采用波动能与波势能相等的原则预测近场区域初始涌浪高度。如王梅力等和袁培银等开展了滑坡初始涌浪物理模型试验，以动能、波势能和压力做功为理论基础，推导出山区河道型水库滑坡涌浪首浪高度计算公式；黄波林等在基于四阶Boussinesq模型的Geo-wave程序基础上，二次开发形成了库区崩塌滑坡涌浪灾害的快速评价系统软件FAST；Xiao等和Zhang等基于体积和动量守恒定律，使用Tsunami Squares滑坡涌浪数值模拟方法实现了滑坡运动与涌浪产生及传播的耦合模拟。因此，在建立滑坡初始涌浪高度预测模型的过程中应充分考虑滑体入水后涌浪的形成机制，使预测模型具有较好的理论基础。

近年来，已有一些学者利用动量守恒定律来分析滑坡涌浪问题。如Zweifel等和Mulligan等以滑体的动量为驱动力，推导出静水平衡和动水平衡的二维滑坡初始涌浪高度的计算公式；韩林峰等在此基础建立了三维滑坡初始涌浪高度的计算公式；汪洋等采用条分法求解滑体运动速度，并使用动量定理求解水库库岸滑坡的初始涌浪高度。上述学者在建立滑坡初始涌浪高度预测模型过程中不同程度地简化了滑坡入水后产生的初始涌浪水面曲线，没有对滑坡近场区域的初始涌浪波形特征做出判断，使计算模型的预测结果与实际情况往往具有一定的差异。因此，有必要对三维滑坡初始涌浪的波形曲线特征做详细研究。为此，本文基于滑坡涌浪物理模型试验，通过非线性波特征分类方法分析高陡库岸滑坡初始涌浪的波形特征，并结合动量定理，建立了适用于高陡库岸三维滑坡的初始涌浪波幅预测模型，提出了修正系数

K

，探讨了修正系数与相对迎水面积和弗劳德数的相关关系，最后通过前人研究成果和工程实例验证了修正后的高陡库岸三维滑坡初始涌浪波幅预测模型的适用性和可靠性。

1 滑坡初始涌浪物理模型试验

1.1 河道模型设计

滑坡初始涌浪物理模型根据重力相似准则设计，与原型保持几何相似、运动相似；考虑物理模型试验的可靠性和场地条件的适用性，将滑坡初始涌浪物理模型的试验比例尺设置为1∶200；根据试验比例尺设计不同几何尺寸的滑块，滑块为以水泥和碎石为材料的混凝土试块。

试验基于高陡库岸段的巫山县和奉节县东侧河道概化模型进行三维滑坡初始涌浪物理模拟，试验在长25 m×宽5 m×高1.2 m的室内试验水池内开展。河道模型横截面为梯形，其中顶宽为1.75 m，底宽为0.75 m，水深为0.35 m，两岸倾角为35°。如图1所示，河道以滑坡入水点为原点(0，0)，河道模型左侧以0 m、0.35 m、0.7 m、1.0 m、1.35 m、1.8 m和2.0 m布置波高采集仪记录河道涌浪产生和传播特性，波高采集仪在河道中线及左侧0.375 m展开；河道模型右侧为涌浪消波区。

图1 滑坡初始涌浪物理模型试验河道波高采集仪平面布置图

1.2 试验设计方案

针对高陡库岸段滑坡体积小、多位于水面高程以上及速度大的特点，结合高陡库岸滑坡资料，统计分析了滑坡的长度、宽度、厚度、速度、水深及库岸倾角的分布特点，确定滑坡的长度、宽度、厚度及速度为滑坡涌浪的主要影响因素，并选取合理的参数开展高陡库岸滑坡初始涌浪物理模型试验(见表1)。通过试验比例尺1∶200制定试验方案，总计33组试验，每组试验做3次，取3次试验值的平均值作为滑坡初始涌浪分析数据。

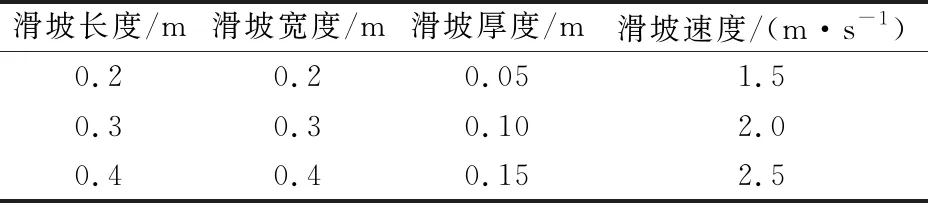
表1 滑坡涌浪的主要影响因素表

1.3 量测仪器与系统

滑坡速度是滑坡初始涌浪物理模型试验中需要准确测量的变量，本试验中主要是通过控制滑块在滑道中的位置来控制滑坡速度，一般将其控制在0～3 m/s之间。利用波高采集仪观测滑坡初始的涌浪高度、周期及速度等要素，该设备采集时间为50 s，采集频率为200 Hz，利用高速摄像机观测滑坡初始涌浪产生的过程。

2 滑坡初始涌浪形成机制

通过观察滑坡刚体入水的过程用来分析近场区域初始涌浪波幅的产生过程，将近场区域初始涌浪波幅的产生过程分为3个阶段(见图2):第一个阶段是滑坡刚体撞击水体，开始受到水体的黏滞阻力，水体受到黏滞阻力的作用后造成雍高，开始形成第一列涌浪波，与此同时在滑坡周围的一小部分表面水体开始脱离水体呈水舌姿态向前运动[见图2(a)]；第二阶段是在水体的黏滞阻力持续作用下，滑体的动量逐渐降低，第一列涌浪波波幅持续增高并以一定的速度向四周传播，脱离水体的水舌进一步向前运动[见图2(b)～(e)]；第三阶段是初始涌浪在四周传播后，周围水体由于快速进入空槽相互碰撞产生巨大的水花团，水花团在碰撞之后能量快速消散，并在滑体周围形成第二列涌浪波[见图2(f)]。

图2 滑坡刚体入水过程

从上述三个阶段得知，滑体快速进入水体后，由于受到水体黏滞阻力的持续作用，滑体速度逐渐降低，第一列涌浪波波幅持续增高，滑体与水体之间的黏滞阻力持续作用产生第一列涌浪波；滑坡后部水体出现空槽，周围水体快速进入空槽后相互碰撞产生第二列涌浪波。故滑坡初始涌浪波产生的原因是在一个相对较短的时间尺度内滑体与水体之间的黏滞阻力作用。

3 滑波初始涌浪波幅预测模型

3.1 滑体入水过程的动量定理

滑坡初始涌浪波的产生过程是滑体动量传递给水体的过程，在一个相对较短的时间尺度内，初始涌浪波的形成是由于滑体与水体之间的黏滞阻力作用。基于动量定理，滑体动量的减少量等于滑体在一定时间内向水体传递的冲量，也等于初始涌浪波的动量，具体表达式如下：

Δ

P

=

P

=

P

1

(1)

P

=

F

Δ

t

cos

α

(2)

P

1=

ρ

V

c

(3)

式中：Δ

P

为滑体入水后在Δ

t

时间内动量的减少量;

P

为滑体向水体传递的冲量(N·s)；

P

1为初始涌浪的动量(kg·m/s)；

F

为滑体与水体之间相互作用的黏滞阻力(N)；Δ

t

为从滑体冲击水面到初始涌浪完整产生的时间(s);

α

为滑动面倾角(°);

ρ

为水体的密度(kg/m);

V

为初始涌浪体积(m);

c

为运动水体的速度(m/s)。

依据公式(1)、(2)和(3)，得到如下公式：

F

Δ

t

cos

α

=

ρ

V

c

(4)

滑体在水体运动中主要受到滑体与水体之间黏滞阻力的影响，在

Δt

(较短的时间尺度)时间内，滑体与水体之间相互作用的黏滞阻力的表达式为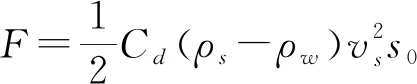

(5)

式中：

C

为水体对滑体的黏滞阻力系数，取值为0

.

15～0

.

18;

ρ

为滑体密度(kg/m);

v

为滑体入水速度(m/s);

s

为滑体的表面积(m)。

3.2 近场区域初始涌浪波形与传播

滑体入水点近场区域产生的初始涌浪具有很强的非线性，高陡库岸滑坡及河道的基本特征为滑坡倾角

α

较大、河道水深

h

较深、滑体厚度

s

较薄、滑体体积不大(质量较小)，而这些因素是容易产生斯托克斯波的必要条件。结合滑坡初始涌浪物理模型试验，认为高陡库岸滑坡产生的初始涌浪波形为斯托克斯波。

基于滑坡初始涌浪物理模型试验，认为近场区域初始涌浪呈半圆状传播(见图2)，初始涌浪波在各径向角度下的波形基本相同，其概化模型见图3。

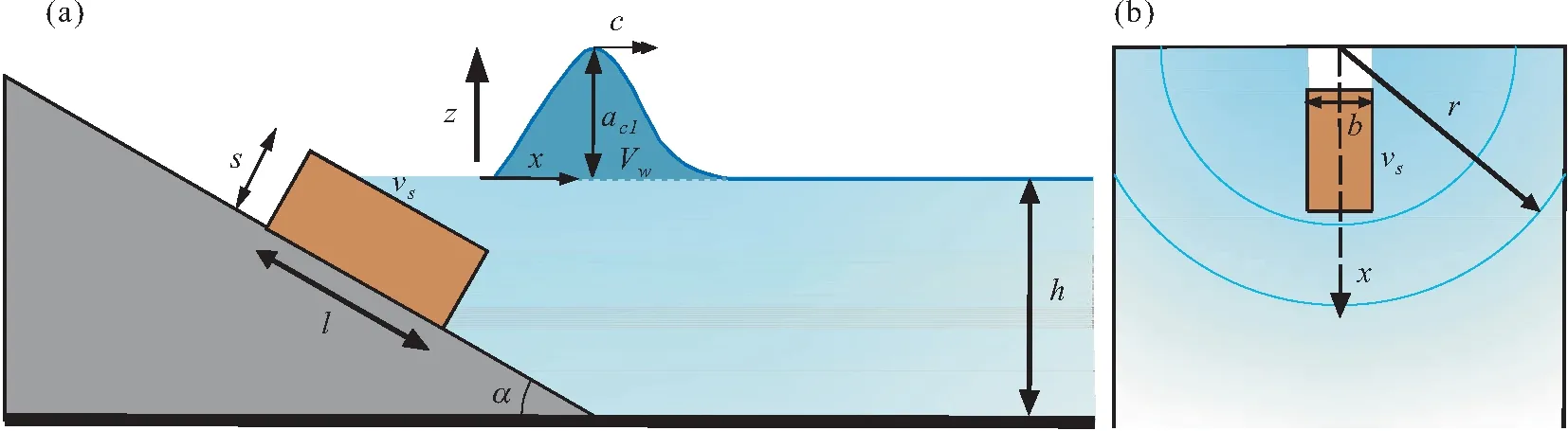
图3 三维滑坡初始涌浪传播示意图(改自Heller等[19])

3.3 滑坡初始涌浪波幅预测模型

斯托克斯波的波峰和波谷大致相等，故二阶斯托克斯波在0 s时的自由水面波动方程为

[2+cos

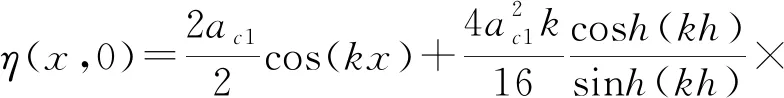
h

(2

kh

)]cos(2

kx

)

(6)

式中：

a

1为初始涌浪波幅(m);

k

=2π/

L

,其中

L

为波长(m)。在产生初始涌浪波幅的时间Δ

t

内，三维滑坡初始涌浪体积的波剖面积为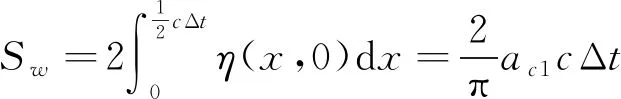

(7)

式中：

S

为三维滑坡初始涌浪体积沿滑块运动方向上的波剖面积(m)。

对三维滑坡初始涌浪体积的波剖面积对弧长曲线积分，则三维滑坡初始涌浪体积为

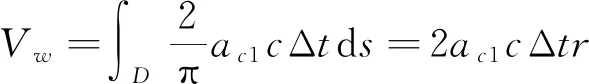
(8)

式中：

D

为三维滑坡初始涌浪波峰在平面上的投影;

r

为初始涌浪波峰投影后在平面上所对应的半径(m)。

浅水重力波波速的计算公式为

c

=(

gh

)12

(9)

式中：

c

为浅水重力波波速(m/s);

g

为重力加速度，其值为9.8 m/s。

将公式(5)、(8)、(9)代入公式(4)中，可得到三维滑坡初始涌浪波幅的理论计算公式如下：

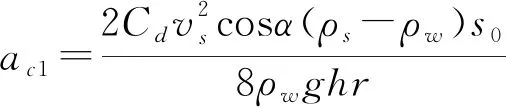
(10)

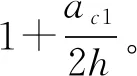
3.4 滑坡初始涌浪波幅预测模型的修正

滑坡初始涌浪波幅预测模型中采用的斯托克斯波理论曲线往往与物理模型试验中产生的初始涌浪波幅曲线具有一定的差异，为了使其适用于高陡库岸的三维滑坡初始涌浪波幅预测模型，并具有更好的适用性，本文引入修正系数

K

对公式(10)进行了修正，具体修正公式如下：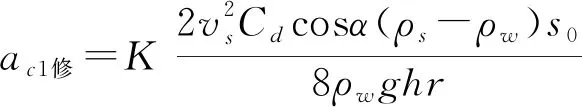

(11)

将33组高陡库岸段滑坡初始涌浪物理模型试验值与修正前的模型预测值进行了拟合，得到各组试验的修正系数

K

值，见图4。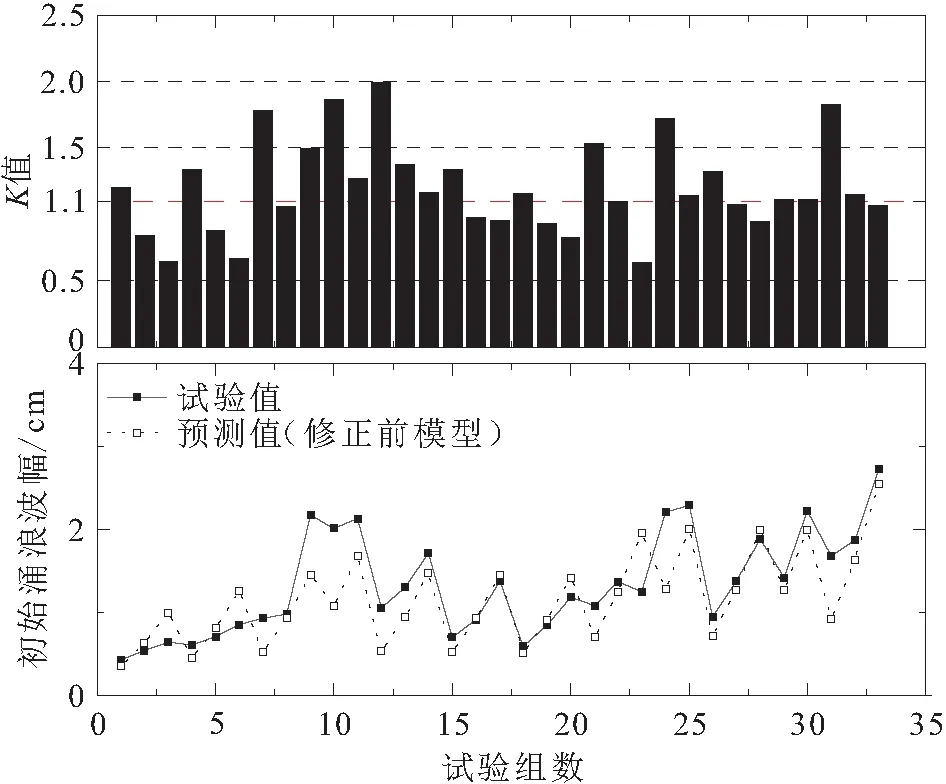

图4 高陡库岸滑坡初始涌浪波幅预测模型的修正系数K值图

由图4可见，所有试验组的修正系数

K

值范围为0.7～2.0，平均值为1.1。

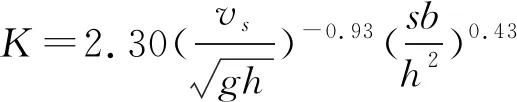
(12)

式中：

s

为滑体厚度(m);

b

为滑体宽度(m);

h

为水深(m)；

v

为滑体入水速度(m/s)。该预测公式(12)中的

K

值与预测模型中的

K

值的相关系数为0

.

820，说明公式(12)能满足对预测模型中

K

值的预测。

4 模型验证分析

本文以龚家方滑坡为工程实例，对修正后的三维滑坡初始涌浪波幅预测模型的适用性和可靠性进行了验证分析。

2008年11月23日16点40分，位于重庆市巫山县巫峡镇龙江村的龚家方滑坡约38×10m的滑坡堆积体滑入长江，并在上下游数公里范围内造成涌浪。龚家方滑坡滑动后轮廓近似于等腰三角形，上部宽度为45 m，临近水面宽度为194 m，轴向长度约为293 m，崩滑体高差为210 m，入水厚度为15 m，滑入水库的滑动面倾角为54°，滑坡体主要由灰岩组成，滑体密度约为2.6×10kg/m。龚家方滑坡滑动时库水位高程为173 m，水深为142 m，见图5和图6。

图5 龚家方滑坡全景图

图6 龚家方滑坡剖面图

龚家方滑坡的相对迎水面积为0.066，弗劳德数为0.315，根据公式(12)读取适用于龚家方滑坡初始涌浪波幅预测模型的修正系数

K

值为2

.

0，则适用于龚家方滑坡的修正后的三维滑坡初始涌浪波幅预测模型为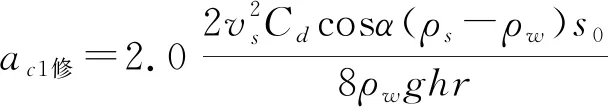

(13)

此外，引入Mulligan等和韩林峰等的滑坡初始涌浪波幅预测模型，对本文修正后的三维滑坡初始涌浪波幅预测模型的合理性进行了验证，3种预测模型对龚家方滑坡初始涌浪波幅计算结果的对比，见表2。

表2 滑坡初始涌浪波幅预测模型计算结果的对比

龚家方滑坡入水速度约为11.65 m/s，造成约31.8 m的初始涌浪高度，初始涌浪高度形成时间约3.8 s。由表2可知，本文预测模型计算得到的龚家方滑坡初始涌浪高度为33.16 m，相对误差为4.29%，比前人研究成果的相对误差要小，说明本文修正后的三维滑坡初始涌浪波幅预测模型具有更好的适用性。

5 结 论

基于高陡库岸三维滑坡初始涌浪波幅理论计算公式，并结合物理模型试验进行验证，得到以下结论：

(1) 从滑坡涌浪的发生机制出发，在一个相对较短的时间尺度内，由于滑体与水体之间的黏滞阻力持续作用，滑体速度逐渐降低，水体产生初始涌浪。通过非线性波特征分类方法综合判别高陡库岸滑坡初始涌浪的波形基本为斯托克斯波。

(2) 以动量定理为基础，运用二阶斯托克斯波的水面曲线方程建立了高陡库岸三维滑坡初始涌浪波幅预测模型，提出了修正系数

K

值，得到了滑坡初始涌浪物理模型试验下的修正系数

K

值的取值范围为0

.

7～2

.

0，平均值为1.1，并探讨了修正系数与相对迎水面积和弗劳德数的相关关系。(3) 以龚家方滑坡为例，根据其相对迎水面积和弗劳德数，得到了适用于龚家方滑坡的修正系数

K

值，建立了适用于龚家方滑坡的高陡库岸三维滑坡初始涌浪波幅的预测模型，并结合前人研究成果验证了该预测模型的适用性和可靠性。结果表明：修正后的三维滑坡初始涌浪波幅预测模型的初始涌浪高度计算结果更准确，相对误差更小。