考虑爆破作用的隧道爆破楔形体稳定性分析
王林峰,胡才龙,曾韬睿,程 平,吴发友
(1. 重庆交通大学 山区公路水运交通地质减灾重庆市高校市级重点实验室,重庆 400047; 2. 重庆交通大学 土木工程学院, 重庆 400047)
0 引 言
目前山区隧道开挖方式主要为新奥法,新奥法主要为钻爆开挖,爆破产生的爆炸应力波随爆心距不同可表现为冲击波、弹塑性应力波、弹性波和地震波。冲击波首先致岩体破碎,消耗大部分能量,接着冲击波衰减为弹塑性应力波及弹性波,最后衰减为地震波,弹性波和地震波虽然不足以导致岩体破碎,但会对有软弱结构面的岩体造成破坏。楔形体是节理面、断层、软弱夹层切割完整岩体形成的岩石块体,在爆破动荷载作用下,楔形体将处于复杂应力状态,可能沿节理面发生坠落和滑移的危险,将危及洞内作业人员及机具安全。目前,在爆破动荷载作用下隧道楔形体稳定性计算仍然是难点,针对爆破荷载作用下楔形体稳定性进行计算分析,对隧道及地下工程设计及施工有一定指导意义。
学者对楔形体的稳定性分析进行了大量的研究。曾宪营等[1]基于Unwedge程序分析了某水工隧道围岩被不同结构面切割条件下的围岩稳定性,并对其进行敏感性分析,认为结构面的内摩擦角、黏聚力及地下水对隧道围岩稳定性的影响较大;郑文海等[2]采用Visual Basic语言编制了赤平投影及实体比例投影程序,能方便判断楔形体的滑动方式,并能根据给定参数计算出锚孔间距及锚杆长度,进一步给出了稳定系数和锚固力的方程及变化曲线;吴发友等[3]基于灰色系统理论建立灰色预警模型,对某隧道洞顶楔形体稳定性进行预测,并通过工程实例表明该方法精度达到了要求;马淑芝等[4]利用结构面三维网络模拟技术,对岩质边坡工程中楔形体进行随机分析和分步筛选,发展了搜索楔形体及其稳定性评价方法,通过实践表明,对于岩质边坡可根据楔形体的几何构成条件,利用楔形体分析方法可从岩体三维结构数字模型中抽取楔形体,并进行稳定性分析;翁其能等[5]基于楔形体极限平衡法,对楔形体进行双折减系数法分析,提出了折减系数增幅比,分析了内摩擦角和黏聚力对楔形体稳定性的影响程度;何昊等[6]利用拟动力法应用于地震荷载计算,揭示了楔形体滑坡在地震作用下的动力响应规律,分析了楔形体滑坡在地震作用下的动力稳定性系数;王瑞红等[7]基于二维,三维极限平衡法并结合赤平投影原理对某泄洪洞口边坡楔形体4种工况下分别进行稳定性分析,结果认为二维极限平衡法计算结果偏于安全,增加了工程造价;A.JOHARI等[8]提出了楔形体系统的可靠性性分析,并进行了敏感性分析,给出了楔形体稳定性曲线;G.ANAGNOSTOU等[9]提出了渗流压力情况的楔形体计算模型,得到了考虑渗流压力工况下的楔形体稳定性计算方法;欧巍[10]基于Hoek 理论采用极限平衡法的分析原理,将地震对楔形体的作用力纳入Hoek理论,得到一种考虑地震作用下楔形体稳定性的计算方法。
由上可知,目前楔形体稳定性分析的方法主要有程序设计、可靠度分析、极限平衡法、块体理论、数值计算等,这些方法丰富了隧道楔形体的稳定性计算研究 。笔者基于前人的研究将采用极限平衡法,并考虑动荷载作用的条件下,推导出隧道动荷载作用下边墙和楔形体稳定系数的计算公式,拟为隧道爆破动荷载作用下楔形体稳定性设计及施工提供理论指导。
1 爆破荷载
震动一般采用振动加速度荷载进行计算和校核,因为振动加速度能和震动产生的惯性力联系,可以直接从加速度记录量出,便于对建筑结构产生影响的地震载荷换算及进行建筑结构内力分析[11]。研究表明,质点震动加速度峰值和与炸药量和爆心距密切相关,据此可确定爆破震动波传到楔形体的加速度峰值[12-13],假定爆破属于一维应力波,由牛顿第二定律有:
amax=158.5(Q1/3/R)2.01
(1)
Fmax=mamax
(2)
式中:amax为质点震动加速度峰值,cm/s2;Q为单响炸药量, kg;R为爆心距,m,指炸药爆破点到待研究位置的距离;m为研究对象的质量, kg;Fmax为研究对象最大爆破惯性力, kN。
由于爆破应力波在传播过程中不仅随距离衰减,还随时间衰减[14],即:
F(t)=Fmaxetη
(3)
式中:t为爆破作用时间,s;η为衰减系数。
2 楔形体稳定性分析
爆炸初始荷载作用于楔形体临空面处,随着爆炸冲击波的传播作用于楔形体的接触面,并产生折射和反射,折射部分随着传播离开楔形体,反射部分会继续作用楔形体,其能量减小且与爆炸荷载的作用方向相反。因此,计算稳定系数需分为作用和反作用两个过程来考虑。
2.1 模型分析基本假设
为采用极限平衡法理论研究隧道围岩楔形体稳定性,作出如下假定:
1)隧道洞顶楔形体为四面体,并考虑为刚体;
2)自然条件下楔形体3个面只受黏聚力,动荷载下3个接触面承受相等的压力或拉力;
3)爆破荷载作用于楔形体重心;
4)楔形体破坏沿接触面滑动,且满足摩尔库伦准则。
2.2 边墙楔形体
隧道边墙物理模型及计算模型如图1,边墙分析时E1F1G1为节理面①,E1F1H1为节理面②,E1H1G1为节理面③,H1F1G1为临空面④,R1为爆心距,O1为重心,β1为滑面倾角。
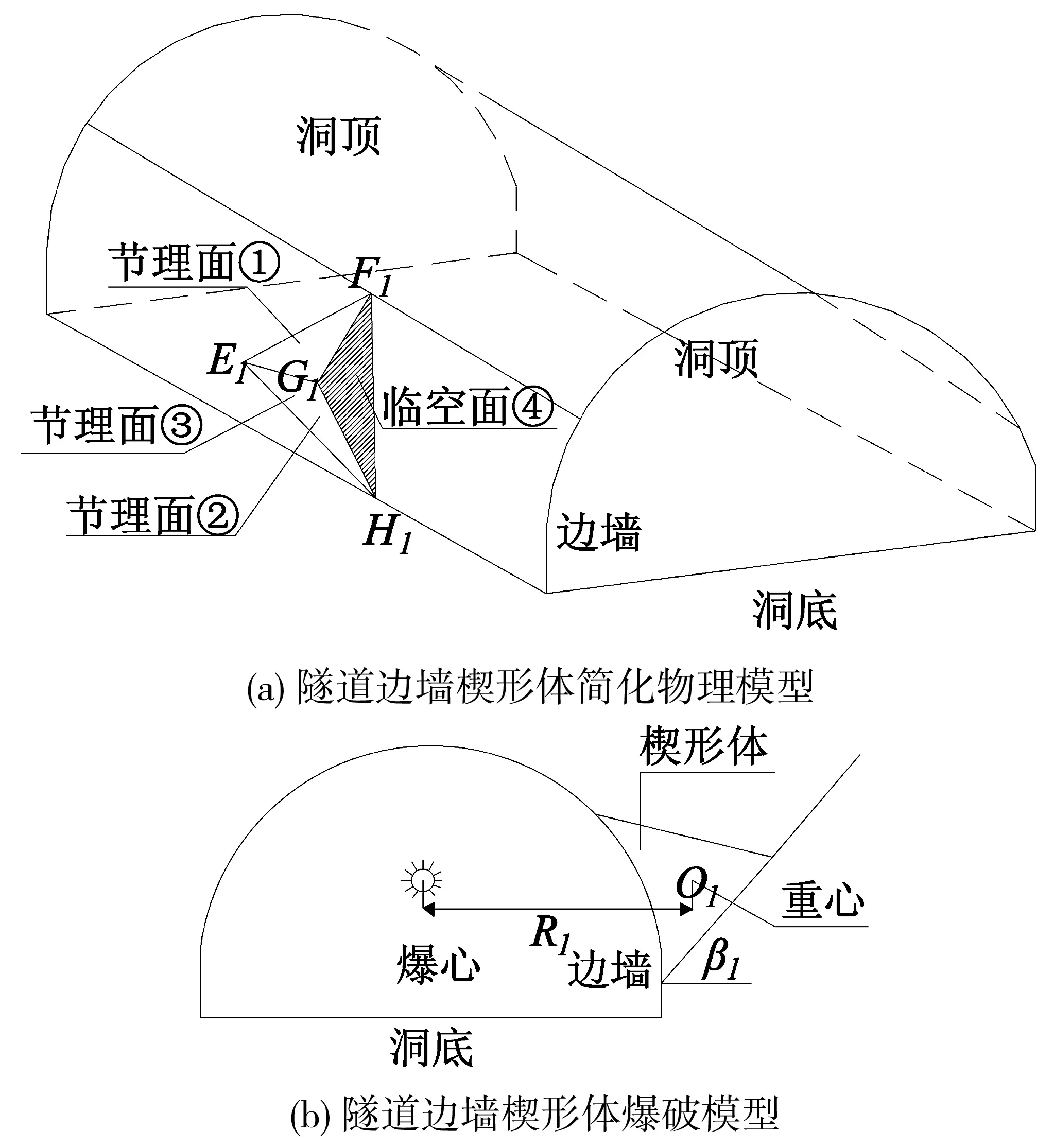
图1 隧道边墙楔形体稳定性分析
2.2.1 边墙单滑面力学分析
爆破惯性力作用于楔形体的重心,沿主控结构面方向分解为法向分量和切向分量。作用过程和反作用过程楔形体的受力状态分析如下。
1)单滑面作用力学分析
边墙单滑面的压力:
Nsz=Wcosβ1+F(t)sinβ1
(4)
边墙单滑面的下滑力:
Tsz=Wsinβ1-F(t)cosβ1
(5)
式中:W为楔形体自重, kN;β1为滑面倾角,(°)。
得到主控结构面的抗滑力:
Fskz=[Wcosβ1+F(t)sinβ1]tanφ+cA
(6)
式中:φ为内摩擦角,(°);c为滑面黏聚力,kPa;A为滑面面积,m2。
2)单滑面反作用力学分析
边墙单滑面反作用时的抗滑力Fskf和下滑力Tsf如下:
Fskf=[Wcosβ1-δF(t)sinβ1]tanφ+cA
在图书馆创客空间运动如火如荼开展的热潮中,学者们对创客空间建设的必要性进行了探讨,主要分为两种观点,一种观点认为建设创客空间非常必要,但也有学者从不同角度提出冷思考。
(7)
Tsf=Wsinβ1+δF(t)cosβ1
(8)
式中:δ为衰减系数。
将两种情况的抗滑力和下滑力代入式(9)即可计算得到两个过程楔形体的稳定系数。
(9)
2.2.2 边墙双滑面力学分析
1)双滑面作用力学分析
节理面①的压力:
(10)
式中:βd为两个节理面交线的倾角,(°),θ1,θ2为节理面①、②的法线与铅垂线夹角, (°)。
节理面②的压力:
(11)
Fdkz=Ndz1tanφ1+Ndz2tanφ2+c1A1+c2A2
(12)
式中:φ1,φ2为节理面①、②的内摩擦角, (°);c1,c2为节理面①、②的黏聚力,kPa;A1,A2为节理面①、②的面积, m2。
下滑力为:
Tdz=Wsinβd-F(t)cosβd
(13)
2)双滑面反作用力学分析
节理面①的压力:
(14)
节理面②的压力:
(15)
即可得到抗滑力为:
Fdkf=Ndf1tanφ1+Ndf2tanφ2+c1A1+c2A2
(16)
反作用下滑力为:
Tdf=Wsinβd+δF(t)cosβd
(17)
将两种情况的抗滑力和下滑力相比,即可计算得到双滑面两个过程楔形体的稳定系数。
2.3 洞顶楔形体
隧道洞顶分析物理模型及计算模型如图2,在洞顶分析时E2F2H2为节理面①,E2G2H2为节理面②,E2F2G2为节理面③,G2F2H2为临空面④,R2为爆心距,O2为重心,β2为滑面倾角。

图2 隧道洞顶楔形体洞顶稳定性分析
2.3.1 洞顶单滑面力学分析
爆破惯性力作用于楔形体的重心,沿主控结构面方向分解为法向分量和切向分量。作用过程和反作用过程楔形体的受力状态分析如下:
1)单滑面作用力学分析
洞顶单滑面抗滑力:
Ftsz=[W-F(t)]cosβ2tanφ2+c3A3
(18)
洞顶单滑面下滑力:
Ttsz=[W-F(t)]sinβ2
(19)
2)单滑面反作用力学分析
单滑面反作用时的抗滑力Ftkf和下滑力Ttsf如下:
Ftkf=[W+δF(t)]cosβ2tanφ2+c3A3
(20)
Ttsf=[W+δF(t)]sinβ2
(21)
将两种情况的抗滑力和下滑力相比即可计算得到双滑面两个过程楔形体的稳定系数。
2.3.2 洞顶双滑面力学分析
1)双滑面作用力学分析
节理面①的压力:
(22)
节理面②的压力:
(23)
由式(23),(24)可得到洞顶双滑面抗滑力:
Ftkz=Ntz1tanφ3+Ntz2tanφ4+c3A3+c4A4
(24)
式中:φ3,φ4为节理面①、②的内摩擦角, (°);θ3,θ4为节理面①、②的法线与铅垂线夹角, (°);c3,c4为节理面①、②的黏聚力,kPa;A3,A4为节理面①、②的面积,m2。
洞顶双滑面下滑力:
Ttdz=[W-F(t)]sinβ2
(25)
2)双滑面反用力学分析
节理面①的压力:
(26)
节理面②的压力:
(27)
洞顶双滑面抗滑力:
Ftkf=Ntf1tanφ3+Ntf2tanφ4+c3A3+c4A4
(28)
洞顶双滑面下滑力:
Ttdf=[W+δF(t)]sinβ2
(29)
将两种情况的抗滑力和下滑力相比即可计算得到双滑面两个过程楔形体的稳定系数。
3 算例分析
采用文献[2]数据对隧道楔形体稳定性进行分析。边墙楔形体容重γ=27 kN·m-3,爆破参数参考文献[11],平均单响药量为48 kg,R=2.5 m,指数衰减参数采用η=-10,楔形体参数详见表1。

表1 楔形体稳定性计算参数
研究在爆破荷载、爆心距,滑面倾角,滑面面积一定的情况下楔形体稳定系数的变化,计算结果表明:边墙楔形体在爆破荷载作用下,楔形体随时间而出现压力和拉力的变化,整个作用时间持续0.3~0.4 s左右。爆破荷载作用下边墙和洞顶的稳定系数有明显的变化,系数增加有利于楔形体稳定,系数减小会严重影响楔形体的稳定性。边墙楔形体在爆破荷载作用下最大峰值荷载达到410.52 kN,最小峰值荷载为-285.69 kN。洞顶楔形体在爆破荷载作用下最大峰值荷载达到140.00 kN,最小峰值荷载为-95.23 kN,结果如图3。
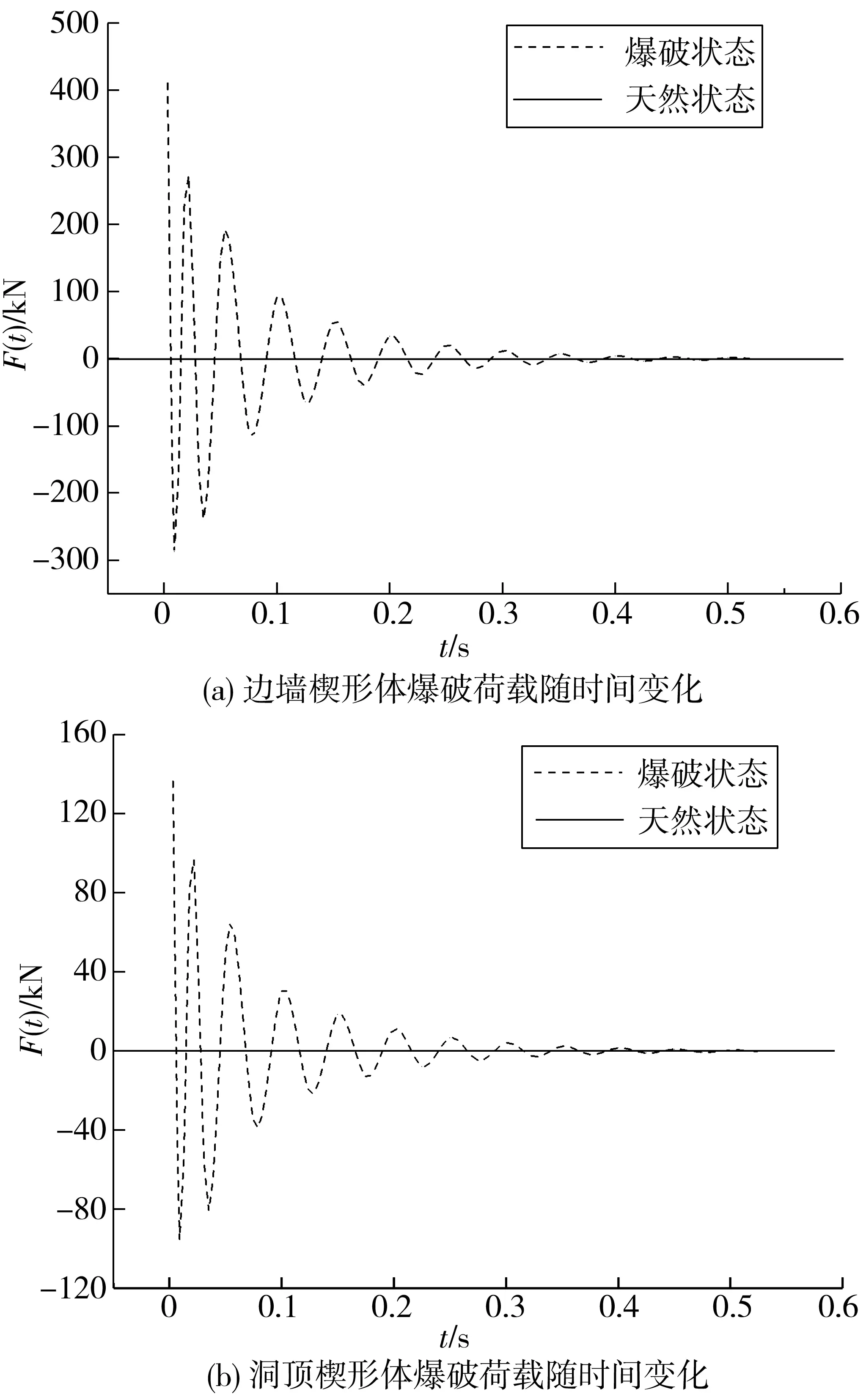
图3 爆破荷载随时间变化
边墙单滑面爆破荷载作用稳定系数最大增加了93.0%,最大减少了63.3%;边墙双滑面稳定系数最大增加了75.0%,最大减小了47.4%。洞顶单滑面在爆破荷载作用下稳定系数最大增加了75.5%,最大减少了56.4%。洞顶双滑面最大增加了81.5%,最大减小了57.8%,结果如图4。

图4 边墙及洞顶不同滑面稳定系数随时间变化
研究爆心距不同对稳定系数的影响,以边墙楔形体进行研究,计算结果表明:在其他条件一定的情况下,爆心距对楔形体有显著的影响,爆心距越小,稳定系数变化范围大;反之,爆心距越大,稳定系数变化越小。当爆心距为2、5 m时,两者稳定系数最大相差1.92,结果如图5。

图5 边墙稳定系数随爆心距变化
计算结果表明,滑面倾角对楔形体稳定影响显著,滑面倾角越小,天然稳定系数越大,滑面倾角越大,天然稳定系数越小。当滑面倾角由28°增加到58°时,稳定系数降低了1.50,爆破对稳定系数的影响最大减小了4.50,计算结果如图6。
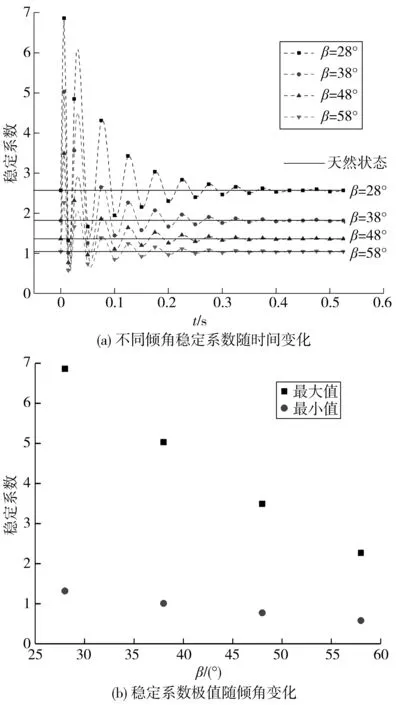
图6 边墙稳定系数随倾角变化
炸药量对稳定系数有显著影响,计算结果表明:在其他条件一定的情况下,炸药量越大,稳定系数增加或减少的绝对值也越大,当炸药量由28 kg增加到58 kg时,稳定系数最大绝对值变化了1.65,如图7。
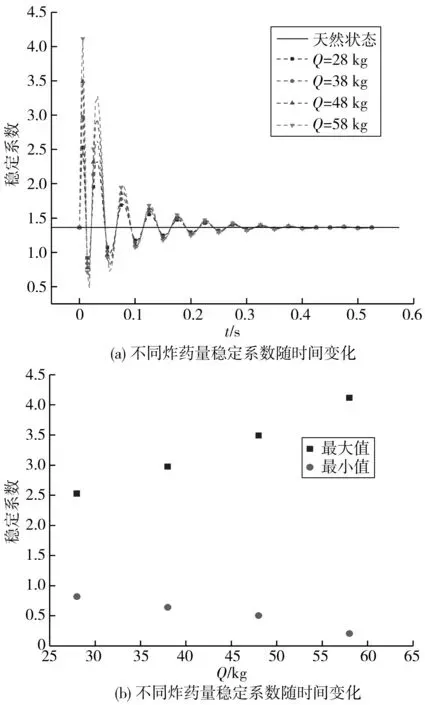
图7 边墙稳定系数随炸药量变化
滑面面积影响楔形体的稳定系数,在其他条件一定时,天然状态下滑面面积越大,稳定系数也越大,爆破条件下,滑面面越大,稳定系数也越大。当面积由8 m2增加到20 m2时,稳定系数最大增加了0.75,结果如图8。

图8 边墙稳定系数随滑面面积变化
4 结 论
通过3个基本假定建立了隧道楔形体危岩的物理模型和计算模型,分析了边墙和洞顶楔形体在单滑面和双滑面条件下的稳定系数。通过爆破振动加速度和牛顿第二定律确定作用于楔形体的峰值荷载,并对峰值荷载进行修正得到时程荷载;结合极限平衡方法得到楔形体静力条件和动力稳定系数,建立了静力和动力条件下稳定系数的计算公式以及不同因素对稳定系数的影响。计算结果表明:
1)边墙楔形体在爆破荷载作用下,楔形体随时间而出现压力和拉力的变化,整个作用时间持续0.3~0.4 s左右。爆破荷载作用下边墙和洞顶的稳定系数有明显增加和降低,增加是有利于楔形体稳定,但减小会严重影响楔形体的稳定性。
2)边墙楔形体在爆破荷载作用下最大峰值荷载达到410.52 kN,最小峰值荷载为-285.69 kN。洞顶楔形体在爆破荷载作用下最大峰值荷载达到140.00 kN,最小峰值荷载为-95.23 kN。
3)边墙单滑面爆破荷载作用稳定系数最大增加了93.0%,最大减少了63.3%;边墙双滑面稳定系数最大增加了75.0%,最大减小了47.4%。洞顶单滑面在爆破荷载作用下稳定系数最大增加了75.5%,最大减少了56.4%。洞顶双滑面最大增加了81.5%,最大减小了57.8%。
4)当爆心距分别为2、5 m时,两者稳定系数最大相差1.92;当滑面倾角由28°增加到58°时,天然稳定系数降低了1.50,爆破对稳定系数的影响最大减小了4.50;当炸药量由28 kg增加到58 kg时,稳定系数最大绝对值变化了1.65;当面积由8 m2增加到20 m2时,稳定系数最大增加了0.75。说明该计算方法是正确合理的。在实际工程中,应采用最小稳定系数来评价楔形体的稳定性。

