对一道绳做功问题的探讨

俞树堂

(民乐县第一中学 甘肃 民乐 734500)

【题目】如图1所示，把A、B两小球从图1中位置同时由静止释放(线开始时拉直)，则两小球向左下摆时，下列说法正确的是

A.线OA对A球做正功

B.线AB对B球不做功

C.线AB对A球做负功

D.线AB对B球做正功

解析：很多人错选B答案，原因是没有分析A、B运动的实际情况而造成的.如果能大致画出A、B球的运动轨迹，那么就可以找出线与球的运动方向的夹角，进而可判定做功的情况.由OA线一直处于张紧且O点不动，所以A球做圆周运动，OA线对A球不做功.而B球是否与A球同步下摆而做圆周运动呢?

图1

参考答案的思路是：设想A、B两球分别用两条细线悬挂而各自摆动，若摆角较小时有摆动周期

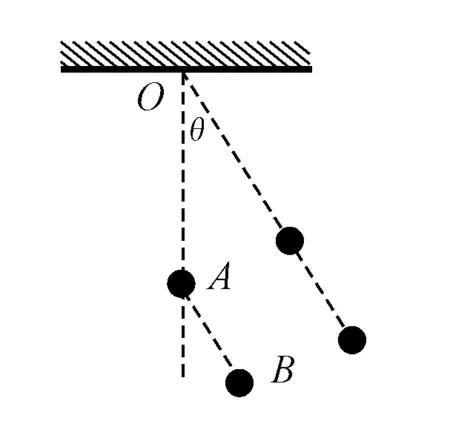
图2

可见摆长越长，摆得越慢，因此A球比B球先到达平衡位置.可见线AB的张力对A球有阻碍运动之作用，而对B球有拉动运动之作用(图2)，所以正确答案为C和D.

笔者认为采用小角度的单摆处理问题，用特殊情形来替代一般情形欠妥.如果从较大角度或水平静止伸直状态自由释放，在以后运动中悬线与两物体有无可能保持共线呢?不妨用铁支架将A、B两球连接起来，然后进行实验，如图3所示，很容易发现线呈折线，AB线是阻碍了A球的运动，加快了B球的运动.因而，对B球做正功，对A球做负功.

在一般情况下的摆所作的摆动，不是简谐运动，而是一种非线性振动，由人教版《物理·必修1教学参考书》相关内容可知这种摆的周期表达式为

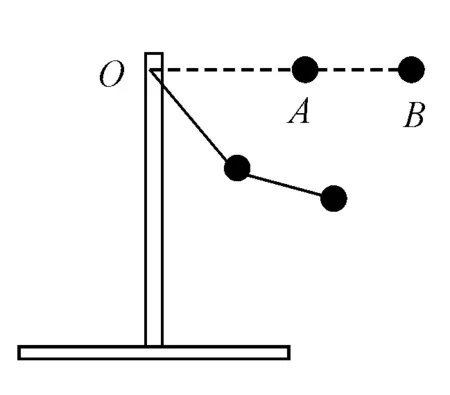
图3

表达式中θ0为摆角，从此表达式可以看出即使在任意摆角下，TB>TA，即A、B下摆时不同步.

图4

严格的证明可采用反证法来进行.令A、B两球的质量分别为m1、m2，OA及AB的线长分别为l1、l2.设系统始终能保持直线状态，那么在转过θ角时系统处于图4所示的方位.两线对质量为m1的A球施加的作用力只能沿直线方向，A球的切向加速度只能来源于m1g的切向分量，即有

m1gcosθ=m1aτ1

因此

aτ1=gcosθ

同理可知，质量为m2的B球的切向加速度为

aτ2=gcosθ

既然两个小球都在做圆周运动，各自对应的角加速度分别为

显然有

β1≠β2

若系统运动过程中始终保持直线状态，便要求恒有β1=β2，于是前后矛盾.因此系统在运动过程中，两线与两小球不可能始终共线.