借题发挥 合作研究
——记一次合作探究学习实践
黄 晶
(嵊州市第一中学 浙江 嵊州 312400)
新课程要求改变课堂教学过于强调接受学习、死记硬背机械训练的现状,倡导学生主动参与、乐于探究、勤于动手,培养学生搜集和处理信息的能力,获取新知识的能力,分析和解决问题的能力以及交流与合作的能力.笔者在此理念的指导下进行了融研究性学习于竞赛教学之中的实践,突出了学生学习方式上的自主性、探究性和合作性,其研究过程及成果记录如下.
1 提出问题
本次探究的问题来源于全国第11届物理竞赛试题:“顶杆AB可以在竖直滑槽K内滑动,其下端由凸轮M推动,凸轮绕O轴以匀角速转动,如图1所示,在图示的瞬时,OA=r,凸轮轮缘与A接触处法线n与OA之间的夹角为α,试求此瞬时顶杆AB的速度.”在解决问题的过程中,有学生开始思考此题的原始背景,认为是从机械传动中提炼而得,进而提出一个问题:“如果凸轮匀角速转动推动顶杆匀速上行,凸轮轮廓应是什么曲线?”

图1
2 猜想假设
鉴于此问题的原创性及自发性,我们将其作为研究性学习的题材分组进行了探索研究.首先是定性分析、猜想假设了曲线的形状.若凸轮轮廓是圆形,则顶杆将静止不动.因此凸轮轮廓应当是一条渐开曲线,猜想可能是椭圆、抛物线、双曲线等常见曲线.
3 设置情景
在实际探究中我们发现直接解决这种传动装置问题比较陌生,起初束手无策.直到后来有小组提出将其转换成熟悉的运动学问题,从而出现转机.经过反复尝试,设置物理情景如下.
有一圆轮在做定轴匀速转动,转速为ω.盘上有一小虫自轮心沿一根幅向轮边做匀速爬行,求解这小虫的运动轨迹方程.
4 解决问题
有很多小组采用了直角坐标系,但求解过程和最终表述都比较复杂.后来有小组查阅资料知此类情境用极坐标解答比较有优势,解答如下.
以地面为参考系,小虫的运动可看成是随轮的转动和沿轮辐的爬行两种运动的合成.选用极坐标系,取固定的盘心O为极点,极轴水平向右.设t=0时,小虫的r=0,φ=0.小虫沿轮辐爬行的速度为v0,则有
vr=v0
以及
vφ=ρ·ω
所以有
v=vri+vφj
从小虫的速度以及初始条件积分,可以求出运动轨迹.
由
两边积分
得
r=v0t
(1)
再由
两边积分
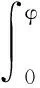
得φ=ωt
(2)
联立(1)、(2)两式消去参数t,得小虫的轨迹方程
5 溯本追源
在小组交流评价环节中,有学生对上述曲线进行了溯本追源,发现它即为阿基米德螺线.
5.1 阿基米德螺线定义
当一点P沿动射线OP等速率运动的同时,这射线又以等角速度绕点O旋转,点P的轨迹称为“阿基米德螺线”,亦称“等速螺线”.因为首次由阿基米德在著作《论螺线》中给出了定义而命名,它的极坐标方程为
r=aφ
其中a为常数.这种螺线的每条臂的距离永远等于2πa.
对于上述设置的物理情景,如果小虫相对于地面参考系以v的速度沿圆的直径运动,那么在相对圆盘静止的转动参考系看来,小虫的轨迹就是一条阿基米的螺线.
5.2 螺线历史
阿基米德在埃及时为了帮助人们解决用尼罗河水灌溉土地的难题,发明了圆筒状的螺旋扬水器,后人称它为“阿基米德螺旋”.阿基米德螺旋实际是一个装在木制圆筒里的巨大螺旋状物,用来把水从一个水平面提升到另一个水平面,对田地进行灌溉.它是现代螺旋泵的前身,直到现在,一些现代工厂仍然使用这种阿基米德螺旋泵来移动流质和粉物.尽管阿基米德螺线是一条古老的曲线,但由于它具有良好的数学、几何、力学和美学性质,所以在凸轮设计、车床卡盘设计、涡旋弹簧、螺纹、蜗杆设计中得到了广泛的应用.
6 实际应用
如图2所示,凸轮绕轴O匀速转动,使杆AB上升.欲使杆AB匀速上升,凸轮上的CD段轮廓线应是什么曲线?

图2
解析:取相对凸轮静止的转动参考系,建立以凸轮中心O为原点,固定在凸轮上的极坐标来研究杆上点A的运动.
根据题意有
(3)
(4)
将式(3)、(4)对时间积分,并设点C为动点A在t=0时的初始位置,于是得以极坐标表示的点A相对于凸轮的运动方程为
θ=ωt
和
r=R+vt
消去时间t,得点在凸轮上的轨迹方程为
从中可以看出凸轮转动时杆AB将匀速上升,则轮廓曲线是阿基米德螺线.
7 提出新问题
在交流评价中有小组还提出新的问题:如果凸轮匀角速转动推动顶杆匀加速上行或简谐运动,凸轮轮廓将分别是什么曲线?
8 教学相长
社会建构主义认为:学习不只是强调个体心智活动的主动性,更应兼及社群与集体之间的互动、磋商、讨论,直至形成共识.这种鲜活的基于合作学习的教学对话既有同能力的伙伴间的水平互动,又有和教师的垂直互动,是平时教学实践中值得我们追寻的.本次合作学习研究采用的是课内讨论和课后研讨相结合的形式,成功之道可以总结为以下三点.
8.1 反思构建了合作学习框架
通过学生自主探究和亲身感受,促使学生在学习中经历了科学探究过程,培养了学生的合作意识、团队协作精神和实事求是的科学态度.在认知过程中激发了学生心灵深处强烈的探索欲望,从而掌握起如下研究物理问题的思路和方法,让探究循序进行(图3).
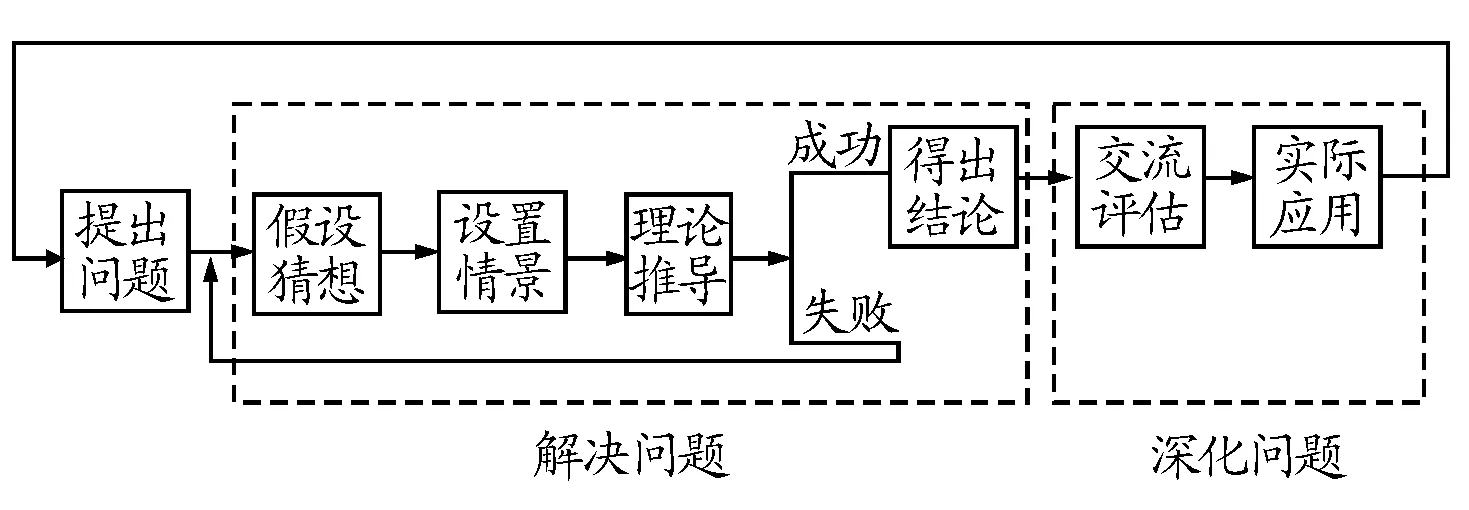
图3
8.2 正确定位了以合作为核心的师生关系
合作学习要求教师充当“指导者”、“合作者”和“促进者”等多种角色,旨在促进整个教学过程的发展,使学生和新知识间的矛盾得到解决.教师不再把自己视作工作者,而是合作者.因为如果教师把自己看作是工作者的话,那么他就会把学生看作是工作的对象,予以机械刺激.在合作学习中,教师与学生之间原有的“权威─服从”关系逐渐变成了“指导─参与”的关系.师生关系如图6所示,其核心是合作.
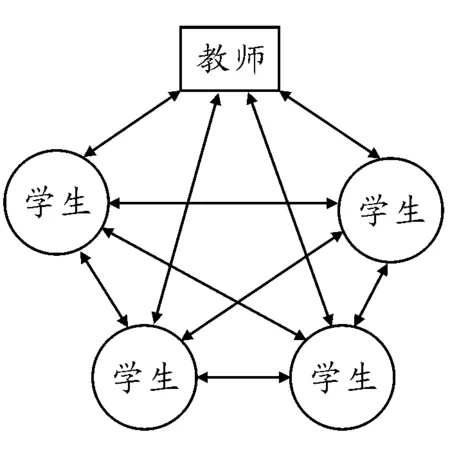
图3
8.3 成功创设了民主活动氛围和多元评价机制
合作学习需要在课堂上营造出平等民主的学习氛围,这使学生感到心理自由和心理安全,唯有如此创造潜能才能得到极大的挖掘,同时学生在认识形成过程中通过同他人交换见解,发现存在着持有不同于自己的见解者,可以从另类观点来思考问题.这样,就使得自己的认识得以相对化.在本次实践中将自评、互评、他评相结合的多元主体评价模式起到了推动探究得以向纵深发展的作用.如本例在研究初期,尝试直接解决问题时普遍感到困难,正是在自评中有小组提出将其情景转化.在直角坐标系求解复杂时,在小组互评中提出优化方案,即采用极坐标.最后写出了完整的学习报告.我们将其成果在校报上刊登加以鼓励.

